概述
本次主要介绍第三部分
时域分析与校正
01
根轨迹
NO.1 根轨迹的作用
由输入输出模型传递函数知，系统的模态和闭环传递函数的解相对应，而闭环传递函数的解的模态由极点决定，因此研究对象转变为了求闭环传递函数的极点。
而根轨迹就是随着参数变化，闭环传递函数极点运动形成的轨迹。
根轨迹能够帮助我们通过手工计算的方式快速地分析系统的性能，此外能够根据性能要求在根轨迹图中确定合适的参数。
NO.2 根轨迹法则的推导
将变量方程借助拉普拉斯变换写成传递函数的形式，有开环传递函数：G0(s)G0(s)，闭环传递函数：G(s)G(s)
如果是负反馈，闭环的特征式是1+G0(s)1+G0(s)那么求闭环特征根，就变成了求解1+G0(s)=01+G0(s)=0的解，改写成G0(s)=−1G0(s)=−1。
提示：可以结合梅森公式进行理解。
s是一个复数，借助复变函数的知识可知即求解G0(s)G0(s)在复平面上幅值为1，幅角为180°的解。如果这个回路是正反馈，闭环的特征方程就变为G0(s)=1G0(s)=1。即求解G0(s)G0(s)在复平面上幅值为1，幅角为0°的解。
所以，称负反馈时的根轨迹为180°根轨迹，而称正反馈时的根轨迹为0°根轨迹。
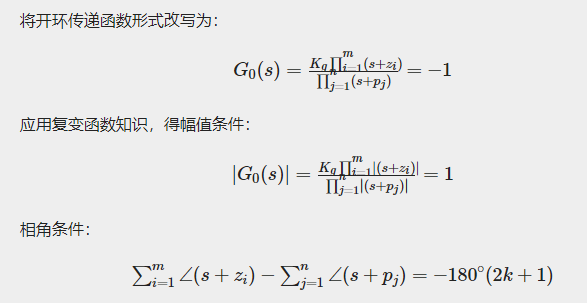
其中幅值条件仅为必要条件，而幅角条件则为充要条件。
提示：具体推导过程请参考《根轨迹法则推导》
NO.3如何看根轨迹图
学会看根轨迹图的关键在于明确解的模态所对应的位置。
稳定性：若根轨迹在正半轴出现，意味着随着时间趋于无穷，该极点对应的模态不会趋于零，因此系统不稳定；
快速性：若根轨迹离虚轴越远，则e−sTe−sT中s越大，该极点对应的模态衰减越快，特别的当根轨迹处于负无穷远处时，对系统的瞬态过程没有影响；
在系统瞬态过程中，变化较慢，过渡时间较长的模态才往往是研究的重点，决定着响应曲线的变化，因此影响系统性能的是那些靠近虚轴部分的根轨迹，距离越近，影响作用越大。
主导极点：距离虚轴最近且周围无闭环零点的极点，而其余极点又远离虚轴，那么对应的响应分量在系统响应中起主导作用，可以选择主导极点将系统降阶。
偶极子：相临近的一对极点和零点，在传递函数中可以近似于零极点对消，因此几乎不会改变根轨迹的形状，即不影响系统的稳定性和瞬态性能，但可以通过它改变开环增益影响稳态性能。
02
稳定性的代数判据
NO.1 如何说明系统的稳定性
对于一个线性定常系统而言，其稳定性完全取决于特征根的位置：
◆当特征根位于左半平面时，系统稳定；
◆当特征根位于虚轴上时，系统临界稳定； ◆当特征根位于右半平面时，系统不稳定；
只要系统有不稳定的特征根，则系统不稳定。
当系统阶数不高时，求解特征方程可以运用代数方法，但是当特征方程次数较高时，代数求解方法极为困难。虽然可以用数值计算的方法求解数值解，但是也增加了很多运算量。
如果对确切数值不关心，而只关心特征根所处的位置，那么则可以用代数学中的方法来研究系统的稳定性，称之为“代数判据”。
NO.2 代数判据具体有哪些
劳斯判据，线性系统渐近稳定的充要条件是：由特征方程系数组成的劳斯表的第一列元素全为正数；若系统不是渐近稳定的，则系统特征方程在右半平面内根的个数等于劳斯表第一列符号改变的次数。
霍尔维茨判据，线性系统渐近稳定的充要条件是：由特征方程系数组成的霍尔维茨行列式的各阶主子式均大于0。
劳斯判据和霍尔维茨判据实质上是一致的，但是霍尔维茨判据涉及矩阵运算，当阶数较大时，运算量急剧上升，因此只对阶数较小的系统采用。
提示：运用劳斯-霍尔维茨判据分析较高次数的特征方程时会出现数值计算稳定性问题。
NO.3代数判据的应用
首要的当然是判别系统的稳定性，除此之外代数判据还有一些其他的应用。
分析系统参数变化对稳定性的影响，由于特征方程的根随特征方程系数的变化而连续地变化，因此可以确定个别参数变化对系统稳定性的影响以及为使系统稳定这些参数的取值范围。
确定系统的相对稳定性，可以用它来说明系统稳定裕度，若特征根全在s=−σs=−σ左边，则称该系统具有σσ的稳定裕度。
03
PID校正
NO.1 如何理解PID校正
串联校正的一种，是对偏差进行微积分的处理以改善系统性能。
PID连续控制：
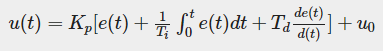
从直观的概念上理解，P是比例，代表现在，I是积分，代表过去，D是微分，代表将来，PID即现在、过去、将来的一种线性组合，所以它能够有效地消除误差，改善系统性能。
提示：一种自适应控制理论能够根据系统的状态在过程中自行调整PID的参数，使性能达到最优。
NO.2PID参数调节的影响
P控制
比例控制器参数与开环增益相关，因此调节它既能够提高系统稳态精度，又可以加快瞬态响应速度，但是过大的开环增益将使系统超调量增加以及使系统的稳定裕度减小，甚至失稳，因此须选择合适的参数；
提示：可以联系根轨迹图进行理解。
I控制
采用积分控制器能够提高系统的型别，消除或减小稳态误差，改善系统的稳态性能，但是也可能会影响系统的稳定性，因此也必须选择合适的参数；
D控制
微分控制器具有预测作用，能够使系统的响应速度加快，超调减小，振荡减轻，但是也可能增加噪声干扰，因此也必须选择合适的参数；
NO.3如何整定PID参数
所有的串联校正环节都可以等效成PID校正，当对象模型已知时，可以通过解析的方法确定PID控制器的参数。
但往往某些对象建模不够精确，甚至无法建模，那么只能根据系统的动态响应来调整PID控制参数。一般采用阶跃或脉冲信号激励被控对象，根据被控对象的过渡过程响应曲线来获得系统的瞬态性能。
常用的方法有：S曲线法，振荡法，衰减曲线法等。
此外，还有PID参数调整口诀可供参考。
提示：由此可以看出PID控制不仅仅适用于“白箱”模型，对大部分“黑箱”模型也同样适用。
—— E N D ——
声明：
ICCE网站所有成果公开，
不盈利，是个兴趣使然的网站。
TR团队期待您的加入！
长
按
关
注
一路同行
ID : gh_ed9aa32d47df
点击原文链接，订阅关注我们.
最后
以上就是爱撒娇河马为你收集整理的串联滞后校正对系统的影响_ICCE 经典控制理论时域分析与校正的全部内容，希望文章能够帮你解决串联滞后校正对系统的影响_ICCE 经典控制理论时域分析与校正所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复