Density Peaks密度峰值聚类算法自动化--平均近邻百分比取密度范围以及outliers探测取聚类中心个数

文章先简单介绍密度峰值聚类算法过程，在聚类过程中详细介绍如何使用平均近邻百分比取密度探测范围，以及后面进行对应的离群值探测。

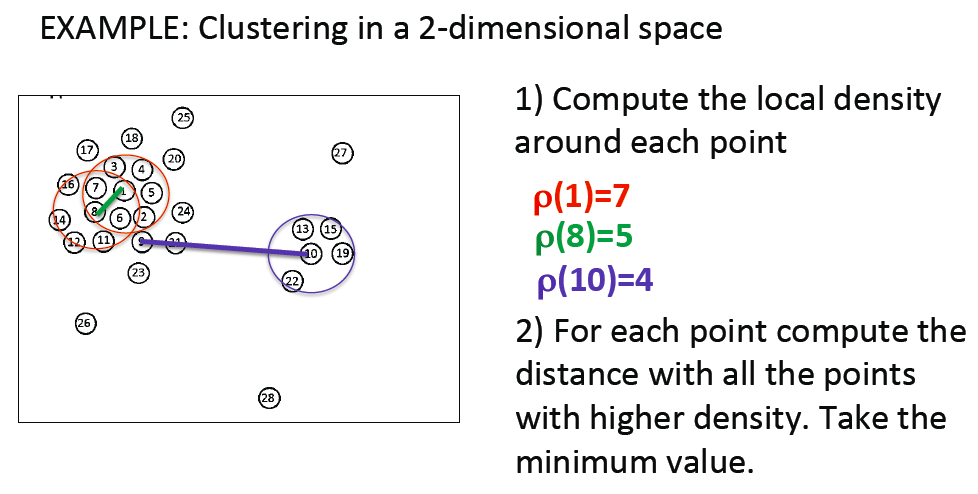
拿一个二维数据举例（上图），对于每一个点，我们计算其到所有其它点的欧几里得距离，取一个密度范围（半径）k，再计算所有点在 k 范围内的密度，即以该点为圆心计算在半径k内有n个其它点的存在，那么n就是其密度。（在这一步上，滕建，乐红兵提出差序密度贡献方法，为减小算法时间复杂度[1]）。

和DBSCAN算法一样，如果不了解数据内容，对于定义半径k确实是一件麻烦事。这里介绍平均近邻百分比取密度范围k值。

举个例子，a(0,0)，b(1,1)，c(2,2)三个点，计算出3个点之间相互的距离: ab-1.4, ac-2.8, bc-1.4一共3组，将这3组距离升序排序，成为[ab, bc, ac]一个长度为3的数列，在该数列里面取长度的第x%的值作为k值，通常来我们取1%-3%，若取第1.5%作为k，在此数列内，即3 x 1.5% = 0.045，四舍五入取整数即为0，在python中，取这个数列的第0个元素，即[ab, bc, ac]得ab，也就是1.4作为k值。

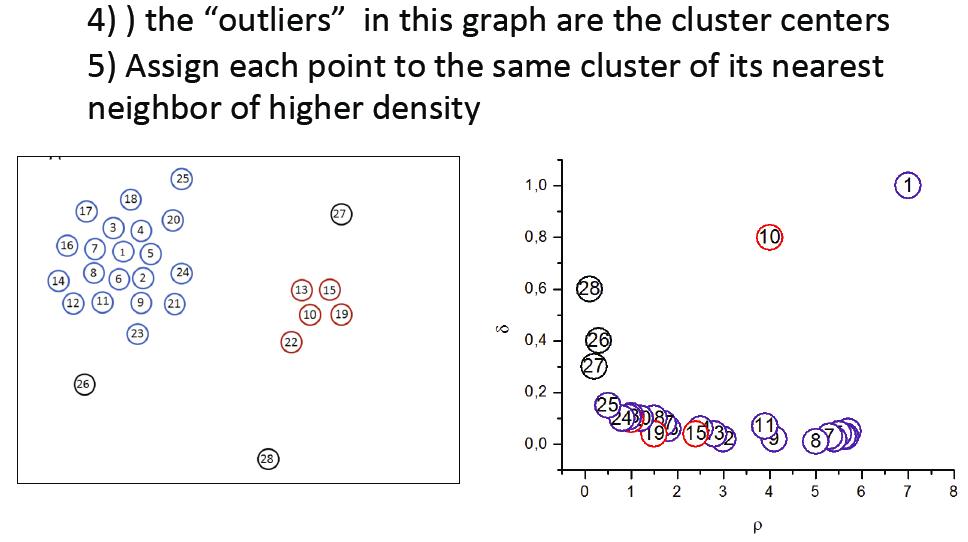
第二步，对刚才计算出来的所有点的密度，找出比该点密度更大的所有点中离该点距离最小的点，并计算两点的欧几里得距离。那么根据第一步的密度，和第二部的距离，得到一个新的二维数组，将其可视为下图中的右手边图（密度-距离图中，将密度最大的点强制更改其坐标为（密度最大值，距离最大值），如图中点1）：

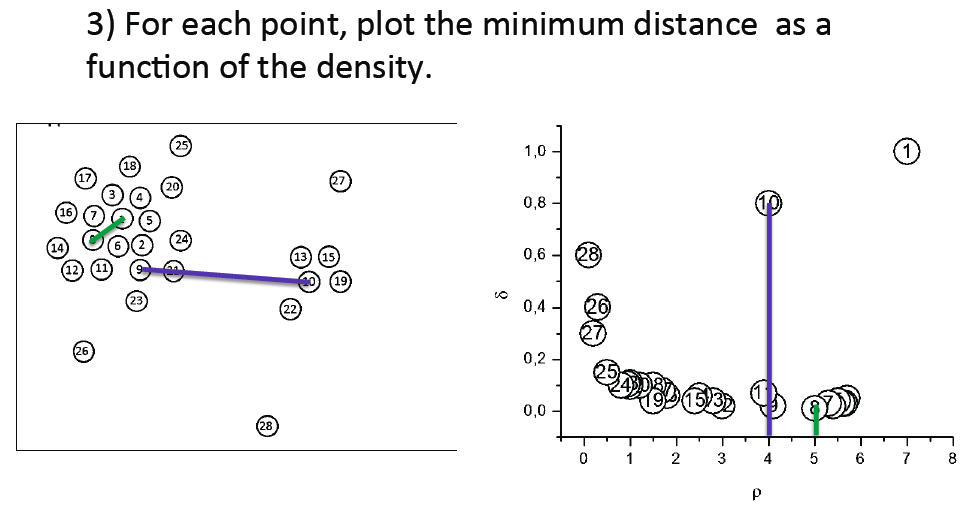
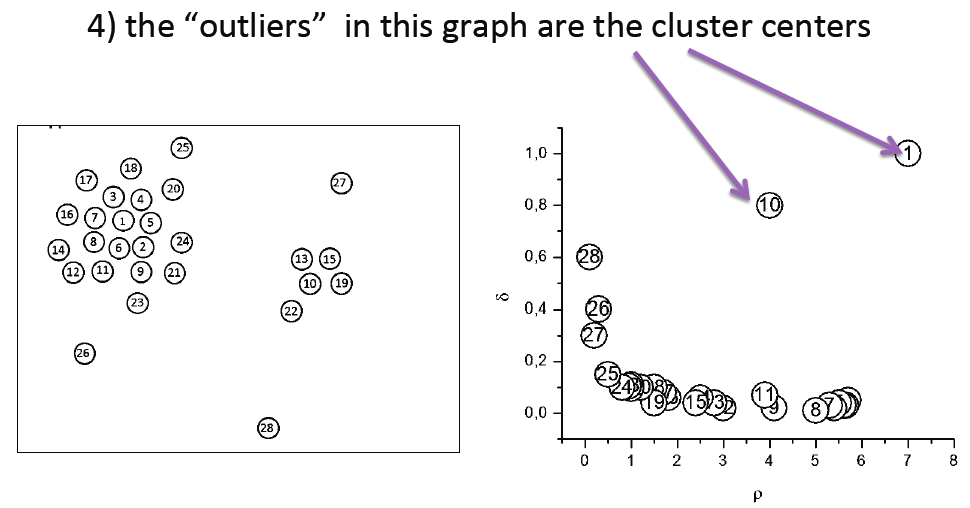
密度-距离图内的outliers即为聚类中心，在例子中选出点1和点10这两个点作为聚类中心，再结合欧几里得距离用最近邻Nearest Neighbor将剩下的点进行类别的分配。这样看确实没什么问题，但当数据量很大的时候，比如点10，可能和点1000重叠，所以肉眼看不到，这时候需要做一个离群值探测。

离群值探测基本上都以距离或相似度作为基准，根据Minkowski距离公式：

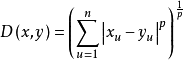
当p→∞时，距离为Chebyshev距离：

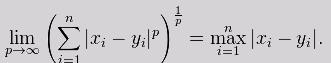
受到Chebyshev距离max|Xi - Yi|启发，在Density Peaks聚类场景下，使用与Chebyshev距离对立的距离公式：

        Min|Xi - Yi|

即在两点中取最短的轴的距离，比如A(1,3), B(4,2), 那么Chebyshev距离为3–（取|1-4|的值），而本文公式计算出的距离为1–（取|3-2|的值）

此距离算法（暂定为Triumph距离）能够计算离原点轴的离散程度，在二维数组来说，设原点为（6，6）如下图，那么在（6，6）做一个新的十字座标轴，图中大多数与原点（6，6）的Triumph距离都很小（范围在0-2），而很明显看到右上角有个outlier（23，23），其与原点的Triumph距离是17。

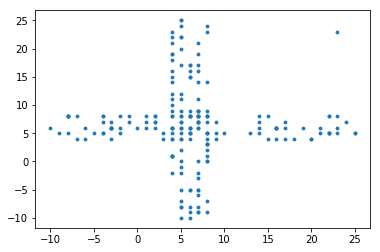
看这张图，根据上面说的Triumph距离，算出上右图所有点离（0，0）Triumph距离后形成一个一维数列，根据这个一维数组，利用Boxplot法或2，3倍标准差法进行离群值探测。

离群值探测–Boxplot箱型图：

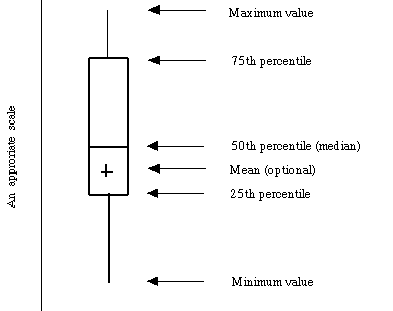
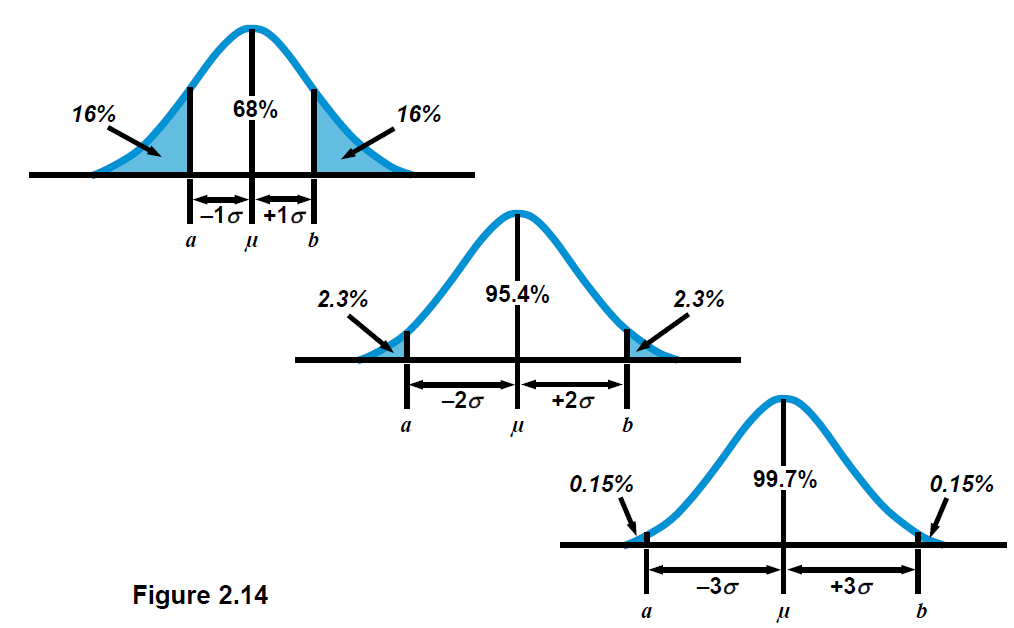
离群值探测–2，3倍标准差法：（σ为标准差）

选出outliers为聚类中心，再结合欧几里得距离用最近邻Nearest Neighbor将剩下的点进行类别的分配，完成聚类。完善整个算法手工操作的弊端。

参考文献：

[1] 滕建, 乐红兵.基于网格的密度峰值聚类算法研究[J].学术研究, 2018:148-150.

最后

以上就是淡然汽车为你收集整理的Density Peaks密度峰值聚类算法自动化--平均近邻百分比取密度范围以及outliers探测取聚类中心个数的全部内容，希望文章能够帮你解决Density Peaks密度峰值聚类算法自动化--平均近邻百分比取密度范围以及outliers探测取聚类中心个数所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。