matlab：分析控制系统稳定性综合实例

matlab/Simulink与控制系统仿真，作者王正林，例5-18，P137，综合实例

clc;clear all
num1 = [20];        %传递函数的分子
den1 = [1 2 0];     %传递函数的分母
sys1 = tf(num1,den1);   %二阶系统的传递函数
num2 = [0.1 0];        %传递函数的分子
den2 = [0 1];     %传递函数的分母
sys2 = tf(num2,den2);   %二阶系统的传递函数
sys_inner = feedback(sys1, sys2);   %内环反馈的传递函数
sys_outer = feedback(sys_inner, 1);   %外环反馈的传递函数
%       20
%   --------------
%   s^2 + 4 s + 20
%进行稳定性分析
den = [1 4 20];         %分母
roots(den)              %求闭环系统特征多项式的根
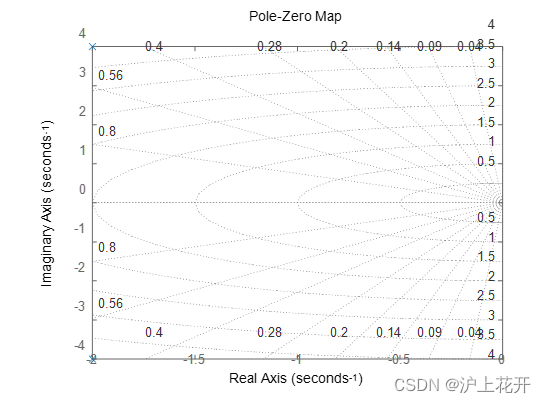
figure(1) 
pzmap(sys_outer);       %绘制系统零极点图
grid on;
%系统特征根均有负实部，因此闭环系统是稳定的
%求阶跃响应
num = [20];
den = [1 4 20];         %分母
[y,t,x] = step(num,den) %计算闭环系统的阶跃响应
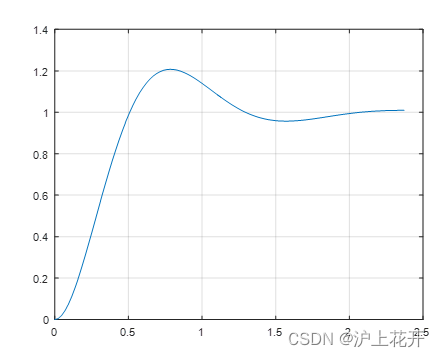
figure(2) 
plot(x,y)
grid on

%分析系统的响应特性
%计算系统的超调量
y_stable =1;            %阶跃响应的稳态值
max_response = max(y);  %闭环系统阶跃响应的最大值
sigma = (max(max_response-y_stable))/y_stable %阶跃响应的超调量

%计算系统的上升时间
for i= 1:length(y)      %遍历响应曲线
    if y(i) > y_stable  %某时刻的输出值大于稳态值
        break;
    end
end
tr = x(i);          %计算此时对应的时间，即上升时间

%计算峰值时间
[max_response, index] = max(y);     %查找阶跃响应的最大值
tp = x(index)                      %计算此时对应的时间，就是阶跃响应的峰值时间

%计算系统的调整时间，取误差带为2%
N = length(y) ;
for i= 1:N      %遍历响应曲线
    if max(y(i:N))<= 1.02*y_stable  %如果当前响应值在误差带内
       if min(y(i:N)) >= 0.98*y_stable
        break;
       end
    end
end
ts = x(i)            %计算此时对应的时间，即调整时间

运行结果：

最后

以上就是寒冷花卷为你收集整理的matlab：分析控制系统稳定性综合实例的全部内容，希望文章能够帮你解决matlab：分析控制系统稳定性综合实例所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。