特征值、特征根、本征值

75 阅读 0 评论 50 点赞

我是靠谱客的博主苹果路灯，最近开发中收集的这篇文章主要介绍特征值、特征根、本征值，觉得挺不错的，现在分享给大家，希望可以做个参考。

狭义特征值问题 Ax = λx
广义特征值问题 Ax = λBx
λ为特征值，x为λ对应的特征向量

在求解特征值时，转化为求解特征多项式|A-λE|=0的特征根

λ在Ax = λx中称为特征值，在 |A-λE|=0中称为特征根

在求解n阶微分方程或差分方程时，先求其对应的特征方程的根(简称特征根)
如二阶微分方程x'' + px' + qx = 0 对应的特征方程 r^2 + p*r + q = 0

在控制方程中也有特征根
二阶微分方程x'' + px' + qx = 0 经过拉氏变换得到特征方程 s^2 + p*s + q = 0

特征方程就是传递函数的分母，特征方程的根称为极点

闭环传递函数 Y(s)/X(s) = G(s)/(1+G(s)*H(s))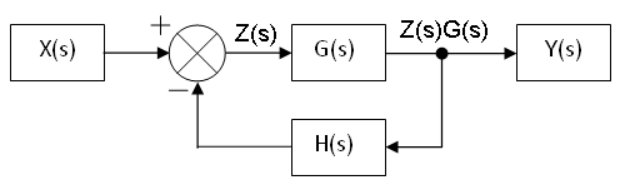

闭环传递函数的特征方程为 1+G*H=0，特征根也称为该传递函数的极点

本征函数与本征值
τ(x) = λx，x称为本征函数，λ称为本征值

其实本征值与特征值一个意思，英文都是eigenvalue

τ()是一个变换，τ(x)可以是Ax，A为矩阵；τ(x)也可以是x''等

我想是不是存在更广义的本征值与本征函数呢即τ(x) = λ*v(x)，τ()与v()都是变换？

以上就是苹果路灯为你收集整理的特征值、特征根、本征值的全部内容，希望文章能够帮你解决特征值、特征根、本征值所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。