3 几个基本的概念以及传递函数
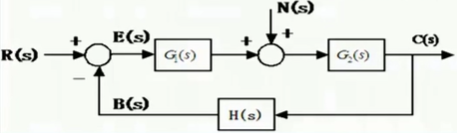
- 前向通道传递函数,顺着系统输入箭头的方向,到达系统输出的通路,且路径中经过的环节不重复。 C ( s ) E ( s ) = G 1 ( s ) ⋅ G 2 ( s ) frac{C(s)}{E(s)}=G_1(s)·G_2(s) E(s)C(s)=G1(s)⋅G2(s)
- 反馈通路的传递函数。 B ( s ) C ( s ) = H ( s ) frac{B(s)}{C(s)}=H(s) C(s)B(s)=H(s)
- *开环传递函数。
B
(
s
)
E
(
s
)
=
G
1
(
s
)
G
2
(
s
)
H
(
s
)
frac{B(s)}{E(s)}=G_1(s)G_2(s)H(s)
E(s)B(s)=G1(s)G2(s)H(s)
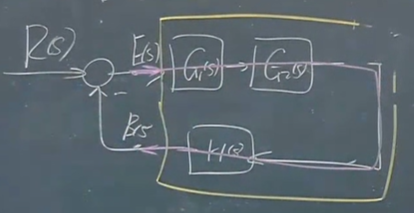
开环传递函数所描述的系统可以看作上图中黄色方框内的部分。它以E(s)作为输入,以B(s)作为输出。可以发现,开环传递函数=前向通道传递函数与反馈通道传递函数的乘积。
知道了开环传递函数的概念,反馈环节的传递函数又可以表示成:
反 馈 环 节 传 递 函 数 = 前 向 通 道 传 递 函 数 1 + 前 向 通 道 传 递 函 数 ⋅ 反 馈 通 道 传 递 函 数 = 前 向 通 道 传 递 函 数 1 + 开 环 传 递 函 数 反馈环节传递函数=frac{前向通道传递函数}{1+前向通道传递函数·反馈通道传递函数}=frac{前向通道传递函数}{1+开环传递函数} 反馈环节传递函数=1+前向通道传递函数⋅反馈通道传递函数前向通道传递函数=1+开环传递函数前向通道传递函数

正反馈同理。
- 闭环传递函数。 C ( s ) R ( s ) frac{C(s)}{R(s)} R(s)C(s)
- *偏差传递函数。
E
(
s
)
R
(
s
)
frac{E(s)}{R(s)}
R(s)E(s)
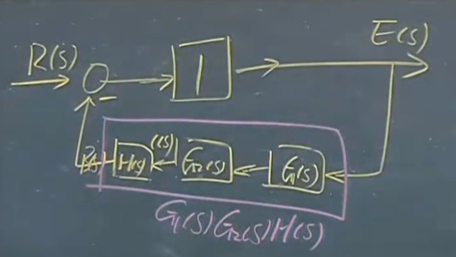
经过上图中的变形,我们可以进一步得到:
E ( s ) R ( s ) = 1 1 + H ( s ) G 1 ( s ) G 2 ( s ) frac{E(s)}{R(s)}=frac{1}{1+H(s)G_1(s)G_2(s)} R(s)E(s)=1+H(s)G1(s)G2(s)1
偏差传递函数与系统闭环传递函数的分母是一样的。 - 输出对扰动的传递函数
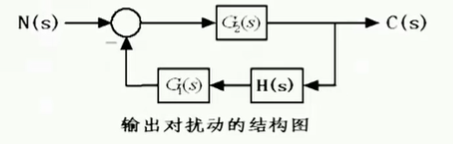
因为此时我们不关注系统原来的输入 R ( s ) R(s) R(s),我们可以暂时将它从框图中抹去,经过变形后,以扰动作为系统输入的框图如上图所示。系统的传递函数表示为: Φ = G 2 ( s ) 1 + G 1 ( s ) G 2 ( s ) H ( s ) Phi=frac{G_2(s)}{1+G_1(s)G_2(s)H(s)} Φ=1+G1(s)G2(s)H(s)G2(s) - 偏差对扰动的传递函数
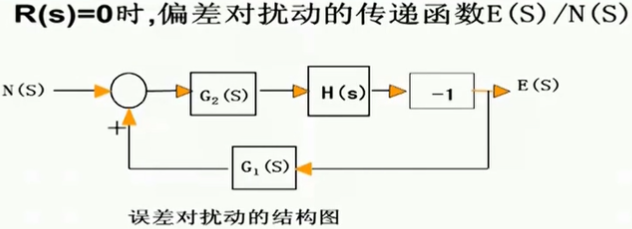
E ( s ) N ( s ) = − G 2 ( s ) H ( s ) 1 + G 1 ( s ) G 2 ( s ) H ( s ) frac{E(s)}{N(s)}=frac{-G_2(s)H(s)}{1+G_1(s)G_2(s)H(s)} N(s)E(s)=1+G1(s)G2(s)H(s)−G2(s)H(s)
此时我们又发现,扰动信号的系统传递函数的分母与闭环传递函数是一样的。
- 通过比较上面给出的不同传递函数我们可以得出结论,对于同一个系统,不同的输入,它们得到的等效传递函数的分母是一样的。
- 任何一个信号点都可以找到它和任意一个输入的传递函数。
- 线性系统满足叠加原理,当系统输入 R ( s ) R(s) R(s)与扰动 N ( s ) N(s) N(s)同时作用于系统时,系统输出等于控制两个变量分别为0时系统响应的叠加。即系统对扰动的传递函数以及对输入的传递函数之和。
4 方框图的绘制
明确系统输入输出,以及系统的传递函数。
将框图中信号相同的位置相连。
MOOC
5 梅森公式与信号流图
如何由方框图得到系统的传递函数,除了等效变换也可以用梅森公式。
前向通路:顺着系统输入箭头的方向,到达系统输出的通路,且路径中经过的环节不重复。
回路/环路: 信号通过每一个基本单元不多于一次的闭合通路称为回路(环路)
回路中经过的所有单元传递函数的乘积(串联)称为回路传递函数,用
L
a
L_a
La来表示。
梅森公式:
Ψ
(
s
)
=
∑
k
=
1
n
P
k
Δ
k
Δ
Psi(s)=frac{sum_{k=1}^n P_k Delta _k}{Delta}
Ψ(s)=Δ∑k=1nPkΔk
公式中
P
k
P_k
Pk代表前向通路的传递函数,假定系统有n条前向通路。

MOOC
最后
以上就是爱笑海燕最近收集整理的关于自动控制原理 学习笔记23 几个基本的概念以及传递函数4 方框图的绘制5 梅森公式与信号流图的全部内容,更多相关自动控制原理内容请搜索靠谱客的其他文章。








发表评论 取消回复