自动控制原理（4）——传递函数、典型环节的传递函数

自动控制原理（4）——传递函数、典型环节的传递函数

微分方程模型

• 优点：是时间域的数学模型，比较直观，它用时间域的方式，描述系统输入和输出变量之间的关系

  ​ 在给定初始条件和输入信号后，借助计算机可以迅速而准确地求出输出响应

• 缺点：不便于分析结构或参数变化对系统性能的影响

微分方程的方法研究控制系统对于参数变化或结构形式的改变的分析具有局限性

一、传递函数

• 复数域的数学模型

• 在研究系统结构或参数变化对性能的影响方面非常方便

• 定义：线性定常系统的传递函数是零初始条件下系统输出量的拉氏变换与系统输入量的拉氏变换之比

• 传递函数针对线性定常系统定义，对非线性的、或时变的系统是不适用的

• 零初始条件

  • 系统的输入在时间t>0时才作用于系统，在零时刻之前，系统的输入及其各阶导数均为零
  • 输入在施加于系统之前，系统为稳态，也就是说，在零时刻之前，系统输出及其各阶导数均为零

• 性质

  • 传递函数反映系统自身固有特性，与输入和初始条件无关

  • 传递函数与微分方程：将微分方程运算符d/dt用复数s置换可以得到传递函数，反之亦然

  • 不同的物理系统可能有相同的传递函数（如相似系统），而同一系统可以有不同的传递函数

  • 一个传递函数只能表示一个输入对一个输出的函数关系，如果是多输入多输出系统，可以用传递函数矩 阵表示

  • 传递函数与单位脉冲响应之间是拉氏变换与拉氏反变换的关系

  • 一般情况下，传递函数分子的阶数m与分母的阶数n满足n≥m（称为物理现实性条件）

• 局限性

  • 只适于线性定常系统的表达
  • 不反映初始状态的信息
  • 不反映系统内部的信息

二、典型环节的传递函数

构成线性定常控制系统的七个环节：比例环节，微分环节，一阶微分环节，二阶微分环节，积分环节，惯性环节，振荡环节

1、比例环节：c(t)=Kr(t) G(s)=K

• K为比例系数
• 比例环节又称无惯性环节或放大环节
• 比例环节既无零点，又无极点
• 性质：比例环节输出与输入成正比，不失真也不滞后
• 实例：理想的杠杆、放大器、测速发电机、电位器等

2、惯性环节

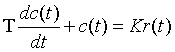
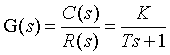
• T为时间常数
• K为放大系数（比例系数）
• 惯性环节无零点
• 性质：当系统输入时单位阶跃信号时系统输出按单调指数规律上升

3、积分环节

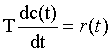
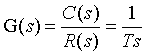
• T为积分时间常数
• 积分环节无零点
• 当输入是单位阶跃信号时，积分环节的输出以固定斜率1/T单调上升

4、振荡环节

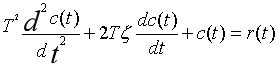
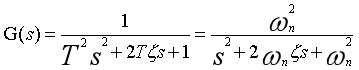
• ω_n为无阻尼自然振荡频率

• ζ为阻尼比

5、微分环节

• 理想微分环节
  
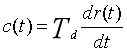
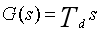
• 微分环节的输出与输入的一阶导数成正比，因此微分环节能预示输入信号的变化趋势，常用来改善控制系统的动态性能

6、一阶微分环节

• 理想一阶微分环节（比例微分环节）
  
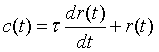
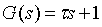
• τ为时间常数
• 比例微分环节可以抑制震荡，提高控制系统的稳定性，改善系统的动态性能

7、二阶微分环节

• 理想二阶微分环节
  
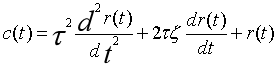
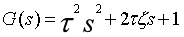
• τ为时间常数
• ζ为阻尼比
• 二阶微分环节没有极点，有2个零点
• 实际中也不存在真正的二阶微分环节

8、延滞环节

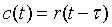
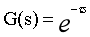
• τ叫做延滞时间，又称死区时间
• 具有延滞环节的系统叫做延滞系统
• 性质：延滞环节将输入延迟τ时间后才输出。系统中存在延滞环节时，对系统的稳定性不利

最后

以上就是感动白昼为你收集整理的自动控制原理（4）——传递函数、典型环节的传递函数的全部内容，希望文章能够帮你解决自动控制原理（4）——传递函数、典型环节的传递函数所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。