实验一:信号与系统的时域分析
- 一:信号的微分与积分
- 积分运算
- 微分运算
- 二:连续时间、离散时间系统的零状态与零输入响应的求解分析
- A:连续时间系统的零状态与零输入响应的求解分析
- 1)零状态响应求解
- 2)零输入响应求解
- B:离散时间系统的零状态与零输入响应的求解分析
- 三:连续时间、离散时间系统冲激响应与阶跃响应的求解分析
- A:连续时间系统冲激响应与阶跃响应的求解分析
- B:离散时间系统冲激响应与阶跃响应的求解分析
- 四:连续时间、离散时间系统的卷积(Convolution)求解
- A:连续时间系统的卷积求解
- B:离散时间系统的卷积求解
- 五:实验部分:
- 实验内容:
- 实验代码及分析
- 1.信号的微分与积分,信号的尺度变化
- 2.连续时间LTI系统的响应
- 3.已知序列求卷积的结果
一:信号的微分与积分
积分运算
对于连续时间信号,其积分运算使用diff函数来完成,其语句格式为
diff(function,'variable',n)
function表示要进行求导运算的信号,variable为求导运算的独立变量,n是求导的阶数,默认一阶导数。
微分运算
对于连续时间信号,其微分运算使用int函数来完成,其语句格式为
int(function,'variable',a,b)
function表示要进行求导运算的信号,variable为求导运算的独立变量,a,b为积分的上下限,a,b忽略时表示求不定积分。
实例:
求
f
(
x
)
=
x
;
f(x)=x;
f(x)=x;的微分与积分
代码:
syms t f2; %定义符号变量
f2=t;
t=-5:5; %定义变量t的范围
subplot(131);
ezplot(f2,t);
title('原函数')
grid on
ylabel('x(t)');
f=diff(f2,'t',1); %对函数f2中的变量t进行一次微分(即求一阶导数)
subplot(132)
ezplot(f,t);
title('微分函数')
grid on
ylabel('x(t)')
f=int(f2,'t'); %对函数f1中的变量t进行积分
subplot(133)
ezplot(f,t);
title('积分函数')
grid on
ylabel('x(t)')

二:连续时间、离散时间系统的零状态与零输入响应的求解分析
A:连续时间系统的零状态与零输入响应的求解分析
1)零状态响应求解
MATLAB提供了一个lsim函数用来求解零初始条件微分方程
基本格式:
y=lsim(sys,f,t)
t表示计算系统响应的抽样点向量,f是系统输入信号向量,sys是LTI系统模型,用来表示微分方程,差分方程和状态方程。
sys调用的格式为:
sys=tf(b,a)
b和a分别表示微分方程的右端和左端的系数向量,例如:对于方程
y
‘
’
(
t
)
+
2
y
′
(
t
)
+
3
y
(
t
)
=
10
c
o
s
2
π
t
y ‘’(t) + 2y '(t) + 3y(t) =10cos2pi t
y‘’(t)+2y′(t)+3y(t)=10cos2πt
b=[1],a=[1 2 3];
代码:
ts=0;te=5;dt=0.01;
sys=tf([1],[1 2 3]);
t=ts:dt:te;
f=10*cos(2*pi*t);
y=lsim(sys,f,t);
plot(t,y);
xlabel('t(s)');ylabel('y(t)');
title('零状态响应')
grid on;

2)零输入响应求解
MATLAB函数:
基本格式:
y = dsolve(eq,cond,'t')
eq='D2y+3*Dy+2*y=0';
cond='y(0)=1,Dy(0)=2';
参数eq 表示各个微分方程,用Dy,D2y,D3y来表示 y 的一阶导数,二阶导数,三阶导数;
参数cond 表示初始条件或者起始条件;
参数 v 表示自变量,默认是变量 t
实例:
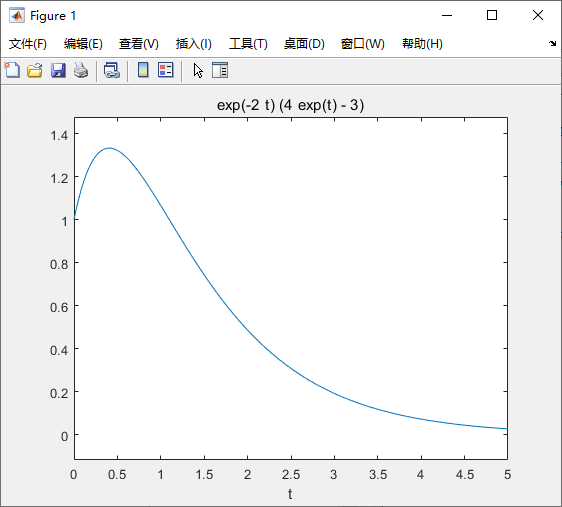
ts=0;te=5;dt=0.01;
t=ts:dt:te;
eq='D2y+3*Dy+2*y=0'; %齐次解求零输入响应
cond='y(0)=1,Dy(0)=2';
yzi=dsolve(eq,cond,'t');
ezplot(yzi,t);
B:离散时间系统的零状态与零输入响应的求解分析
三:连续时间、离散时间系统冲激响应与阶跃响应的求解分析
A:连续时间系统冲激响应与阶跃响应的求解分析
在MATLAB中,求解冲激响应与阶跃响应可以使用函数 impluse 与 step ,详细的内容可以使用帮助系统查看
基本形式:
sys=tf(b,a);
h=impulse(sys,t); %冲激响应
g=step(sys,t); %阶跃响应
b和a分别表示微分方程的右端和左端的系数向量
实例:
求解下面信号的冲激响应
y
"
(
t
)
+
2
y
′
(
t
)
+
3
y
(
t
)
=
u
(
t
)
,
t
>
0
y"(t)+2y'(t)+3y(t)=u(t),t>0
y"(t)+2y′(t)+3y(t)=u(t),t>0
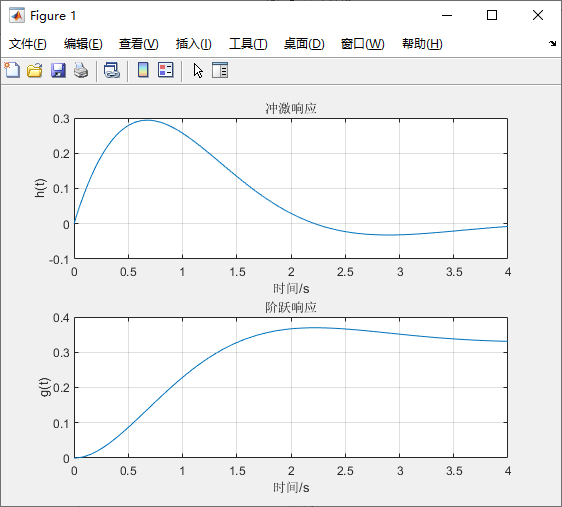
求解代码:
t=0:0.002:4;
sys=tf([1],[1 2 3]);
h=impulse(sys,t); %冲激响应
g=step(sys,t); %阶跃响应
subplot(2,1,1);plot(t,h);
grid on;
xlabel('时间/s');ylabel('h(t)');
title('冲激响应');
subplot(2,1,2);plot(t,g);
grid on;
xlabel('时间/s');ylabel('g(t)');
title('阶跃响应');
B:离散时间系统冲激响应与阶跃响应的求解分析
四:连续时间、离散时间系统的卷积(Convolution)求解
A:连续时间系统的卷积求解
对于连续时间信号,其卷积运算使用conv函数来完成,卷积积分需要乘以步长dt
基本格式:
f=conv(f1,f2)*dt;
f为卷积之后返回的结果(信号),f1,f2都是进行卷积运算的信号
连续信号的卷积积分定义为
f
(
x
)
=
f
1
(
t
)
∗
f
2
(
t
)
=
∫
−
∞
∞
f
1
(
τ
)
f
2
(
t
−
τ
)
d
τ
f(x)=f_{1}(t)*f_{2}(t)=int_{-infty}^{infty} f_{1}(tau )f_{2}(t-tau)dtau
f(x)=f1(t)∗f2(t)=∫−∞∞f1(τ)f2(t−τ)dτ
实例:
求
f
1
(
t
)
=
u
(
t
)
−
u
(
t
−
2
)
,
f
(
2
)
=
2
e
t
u
(
t
)
f_{1}(t)=u(t)-u(t-2),f(2)=2e^{t} u(t)
f1(t)=u(t)−u(t−2),f(2)=2etu(t)
的卷积积分
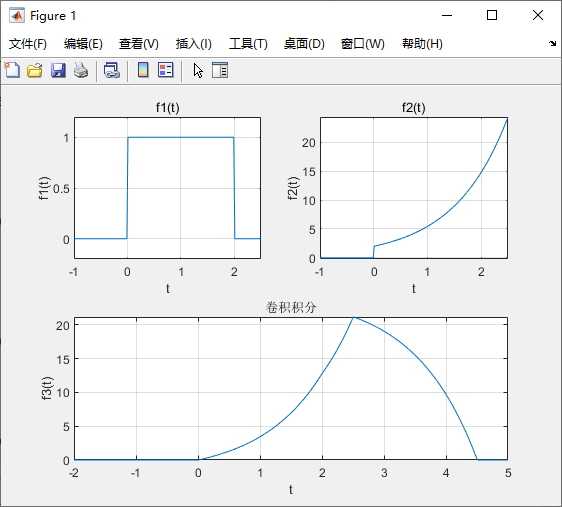
代码:
%/ 连续时间信号的卷积
dt=0.01; t=-1:dt:2.5;
f1=heaviside(t)-heaviside(t-2);
f2=2*exp(t).*heaviside(t);
f=conv(f1,f2)*dt; n=length(f); tt=(0:n-1)*dt-2;
subplot(221);
plot(t,f1);
grid on;
axis([-1,2.5,-0.2,1.2]);
title('f1(t)');
xlabel('t'); ylabel('f1(t)');
subplot(222);
plot(t,f2);
grid on;
axis([-1,2.5,-0.2,1.2]);
title('f2(t)');
xlabel('t'); ylabel('f2(t)');
subplot(212);
plot(tt,f);
grid on;
title('卷积积分');
xlabel('t'); ylabel('f3(t)');
B:离散时间系统的卷积求解
基本格式:
c=conv(a,b);
a、b分别是待卷积的两序列的向量表示,c是卷积结果;向量c的长度为向量a、b的长度之和减1,即
length(c)=length(a)+length(b)-1
离散时间信号的卷积定义为:
f
[
k
]
=
f
1
[
k
[
∗
f
2
[
k
]
=
∑
m
=
−
∞
∞
f
1
[
m
]
f
2
[
k
−
m
]
f[k]=f_{1}[k[*f_{2}[k]= sum_{m=-infty}^{infty} f_{1}[m]f_{2}[k-m]
f[k]=f1[k[∗f2[k]=m=−∞∑∞f1[m]f2[k−m]
实例:已知序列求卷积的结果
x=[1,3,5,7];
y=[1,1,1,1];
z=conv(x,y);
subplot(131);
stem(0:length(x)-1,x);
grid on
subplot(132);
stem(0:length(y)-1,y);
grid on
subplot(133);
stem(0:length(z)-1,z);
grid on
五:实验部分:
实验内容:
-
画出 f ( t ) = ( 2 + t ) ( ξ ( t ) − ( ξ ( t − 3 ) ) 、 f ( t 2 − 1 ) 、 f ( t ) f(t)=(2+t)(xi (t)-(xi(t-3))、f(frac{t}{2} -1)、f(t) f(t)=(2+t)(ξ(t)−(ξ(t−3))、f(2t−1)、f(t) 微分和积分的波形图。
-
已知某连续因果LTI系统的微分方程为 y " ( t ) + 7 y ′ ( t ) + 12 y ( t ) = x ( t ) , t > 0 , x ( t ) = u ( t ) y"(t)+7y'(t)+12y(t)=x(t),t>0,x(t)=u(t) y"(t)+7y′(t)+12y(t)=x(t),t>0,x(t)=u(t)
初始状态 y ( 0 − ) = 1 , y ′ ( 0 − ) = 2 y(0^{-})=1,y'(0^{-})=2 y(0−)=1,y′(0−)=2
用matlab求零输入响应和冲激响应h(t) 。 -
计算卷积 x [ k ] ∗ y [ k ] x[k]*y[k] x[k]∗y[k] ,并画出卷积结果。已知 ,
x [ k ] = { 1 , 2 , 2 , 1 ; k = 0 , 1 , 2 , 3 } , y [ k ] = { 2 , 3 , 1 ; k = 0 , 1 , 2 } x[k]=left {1,2,2,1;k=0,1,2,3 right } ,y[k]=left { 2,3,1;k=0,1,2 right } x[k]={1,2,2,1;k=0,1,2,3},y[k]={2,3,1;k=0,1,2}
实验代码及分析
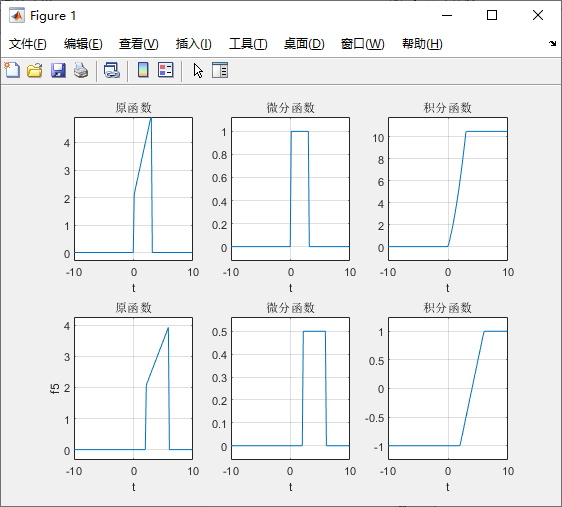
1.信号的微分与积分,信号的尺度变化
代码:
syms t f2;
f0=heaviside(t)-heaviside(t-3);
f1=2+t;
f2=f0.*f1;
t=-10:10;
subplot(231);
ezplot(f2,t);
title('原函数')
grid on
f=diff(f2,1);
subplot(232);
ezplot(f,t);
title('微分函数')
grid on
f=int(f2,'t');
subplot(233);
ezplot(f,t);
title('积分函数')
grid on
syms t f5;
T=(t-2)/2;
f3=heaviside(T)-heaviside(T-2);
f4=T+2;
f5=f3.*f4;
subplot(234);
t=-10:10;
ezplot(f5,t);
xlabel('t');ylabel('f5');
title('原函数')
grid on
f5=diff(f5,1);
subplot(235);
ezplot(f5,t);
title('微分函数')
grid on
f5=int(f5,'t');
subplot(236);
ezplot(f5,t);
title('积分函数')
grid on
运行结果:
2.连续时间LTI系统的响应
求解零输入响应代码:
ts=0;te=5;dt=0.01;
t=ts:dt:te;
eq='D2y+7*Dy+12*y=0'; %齐次解求零输入响应
cond='y(0)=1,Dy(0)=2';
yzi=dsolve(eq,cond,'t');
yzi=simplify(yzi);
ezplot(yzi,t);
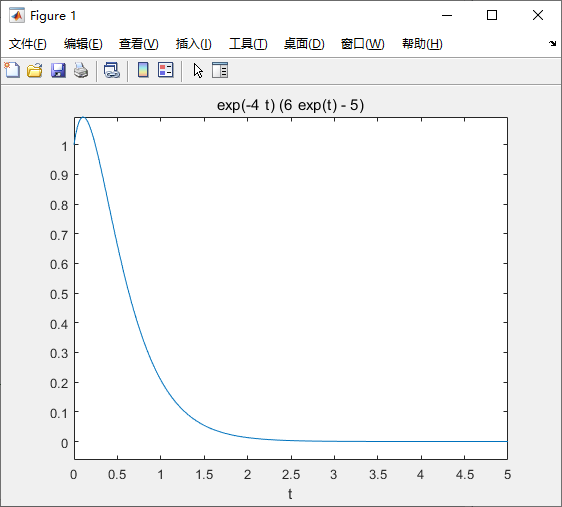
求解冲激响应代码:
t=0:0.002:4;
sys=tf([1],[1 7 12]);
h=impulse(sys,t); %冲激响应
g=step(sys,t); %阶跃响应
subplot(2,1,1);plot(t,h);
grid on;
xlabel('时间/s');ylabel('h(t)');
title('冲激响应');
subplot(2,1,2);plot(t,g);
grid on;
xlabel('时间/s');ylabel('g(t)');
title('阶跃响应');

3.已知序列求卷积的结果
代码:
x=[1,2,2,1];
y=[2,3,1];
z=conv(x,y);
subplot(131);
stem(0:length(x)-1,x);
grid on
subplot(132);
stem(0:length(y)-1,y);
grid on
subplot(133);
stem(0:length(z)-1,z);
grid on
运行结果:

最后
以上就是谨慎皮卡丘最近收集整理的关于信号与系统——MATLAB信号处理——信号与系统的时域分析五:实验部分:的全部内容,更多相关信号与系统——MATLAB信号处理——信号与系统内容请搜索靠谱客的其他文章。








发表评论 取消回复