位置式PID算法
{
e
r
r
o
r
(
k
)
=
r
i
n
(
k
)
−
y
o
u
t
(
k
)
x
(
1
)
=
e
r
r
o
r
(
k
)
x
(
2
)
=
x
(
2
)
+
T
s
∗
e
r
r
o
r
(
k
)
x
(
3
)
=
e
r
r
o
r
(
k
)
−
e
r
r
o
r
(
k
−
1
)
p
i
d
=
[
K
p
K
i
K
d
]
u
(
k
)
=
p
i
d
∗
x
begin{cases}error(k)=rin(k)-yout(k) \x(1)=error(k) \x(2)=x(2)+Ts*error(k)\x(3)=error(k)-error(k-1)\pid = [K_p :K_i:K_d]\u(k)=pid*xend{cases}
⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧error(k)=rin(k)−yout(k)x(1)=error(k)x(2)=x(2)+Ts∗error(k)x(3)=error(k)−error(k−1)pid=[KpKiKd]u(k)=pid∗x
u
(
k
)
u(k)
u(k)为控制量相当于状态量x与pid参数的线性组合，为了动态调整pid参数构建一个单神经元网络，性能指标函数取
J
=
∑
(
r
i
n
(
k
)
−
y
o
u
t
(
k
)
)
2
/
2
J=sum(rin(k)-yout(k))^2/2
J=∑(rin(k)−yout(k))2/2;根据梯度下降法调整pid参数，即
Δ
K
p
=
−
η
∂
J
∂
K
p
Delta K_p=-etafrac{partial J}{partial K_p}
ΔKp=−η∂Kp∂J,这个怎么求偏导？
Δ
K
p
=
−
η
∂
J
∂
K
p
=
−
η
∂
J
∂
y
o
u
t
∂
y
o
u
t
∂
Δ
u
∂
Δ
u
∂
K
p
=
η
.
e
o
r
r
o
r
(
k
)
.
x
(
1
)
.
∂
y
o
u
t
∂
Δ
u
Delta K_p=-etafrac{partial J}{partial K_p}=-etafrac{partial J}{partial yout}frac{partial yout}{partial Delta u}frac{partial Delta u}{partial K_p}=eta .eorror(k).x(1).frac{partial yout}{partial Delta u}
ΔKp=−η∂Kp∂J=−η∂yout∂J∂Δu∂yout∂Kp∂Δu=η.eorror(k).x(1).∂Δu∂yout,利用RBF网络的逼近能力，识别系统的Jacobian阵，即
∂
y
o
u
t
∂
Δ
u
frac{partial yout}{partial Delta u}
∂Δu∂yout。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76function [sys,x0,str,ts,simStateCompliance] = PID_RBF_s(t,x,u,flag) % 网络结构3-6-1 % 采样时间 Ts = 0.001; switch flag case 0 [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes(Ts); case 2 sys=mdlUpdate(x,u,Ts); case 3 sys=mdlOutputs(t,x,u); case {1,4,9} sys=[]; otherwise DAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag)); end function [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes(Ts) sizes = simsizes; sizes.NumContStates = 0; sizes.NumDiscStates = 3; sizes.NumOutputs = 2; sizes.NumInputs = 4; sizes.DirFeedthrough = 1; sizes.NumSampleTimes = 1; sys = simsizes(sizes); x0 = [0;0;0]; str = []; ts = [Ts 0]; simStateCompliance = 'UnknownSimState'; function sys=mdlUpdate(x,u,Ts) sys=[u(1); x(2) + u(1)*Ts; (u(1) - u(2))]; function sys=mdlOutputs(t,x,u) persistent w w_1 w_2 h c PID_parm % PID三个三个参数学习效率 xitePID = [1 1 1]; % RBF网络学习效率 xite = 0.5; % RBF网络动量因子 alfa = 0.5; % 高斯基函数宽度 b = 3; if t == 0 % PID参数初值 PID_parm = [0.7 0 1]; % 高斯基函数中心矩阵，取值范围在输入信号范围内 c = [linspace(-1,1,6);linspace(0,1,6);linspace(0,1,6)]; h = zeros(6,1); w = zeros(6,1); w_1 = w; w_2 = w_1; end uu = PID_parm*x; RBF_input = [uu u(3) u(4)]'; for j = 1:6 h(j) = exp(-norm(RBF_input - c(:,j))^2/(2*b^2)); end ymout = w'*h; d_w = xite*(u(3) - ymout)*h; w = w_1 + d_w + alfa*(w_1 - w_2); yu = w.*h.*(-RBF_input(1) + c(1,:))'/b^2; % Jacobian阵 dyout = sum(yu); PID_parm = PID_parm + u(1)*dyout*x'.*xitePID; w_2 = w_1; w_1 = w; sys = [uu;ymout];
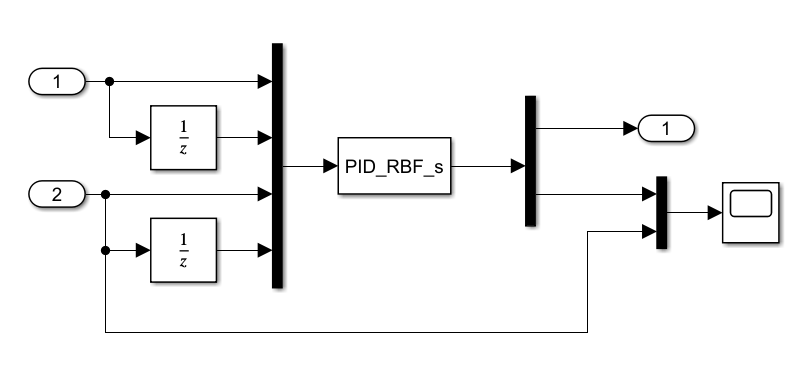
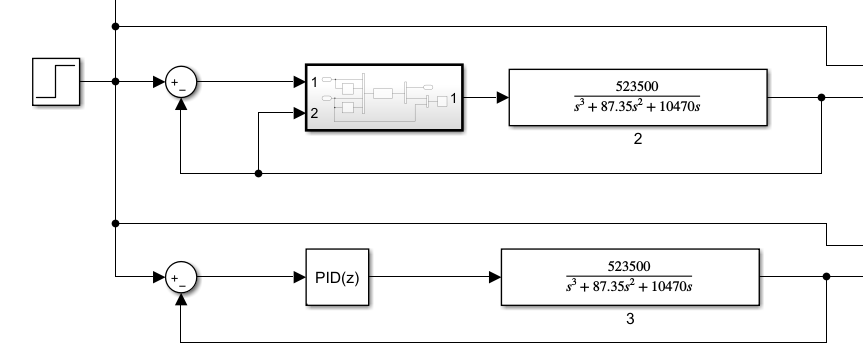
最后
以上就是风趣西牛最近收集整理的关于RBF-PID的s-function实现以及Simulink的模块封装的全部内容，更多相关RBF-PID内容请搜索靠谱客的其他文章。
发表评论 取消回复