一、实验目的
1. 掌握各数学模型之间的转换与数学模型的参数获取,掌握相关MATLAB命令
2. 掌握欧拉法和RK法的递推公式
3. 掌握欧拉法和RK法的MATLAB算法实现
二、实验内容
1. 分别用欧拉法和四阶龙格-库塔法求解如下系统:
(1) R=4KΩ, C=1µF, L=1H, 仿真时间: 0.03s
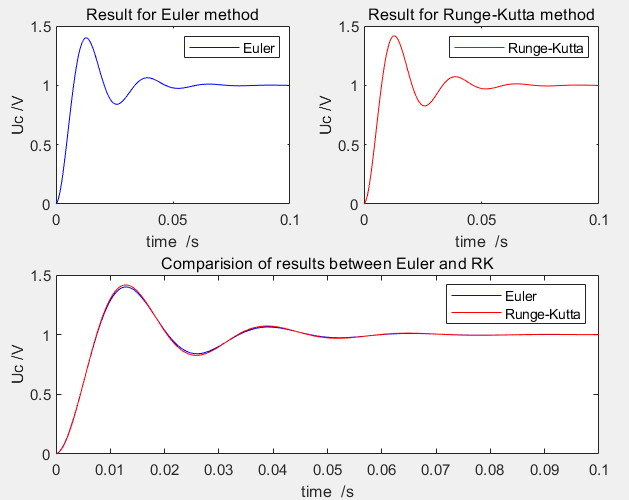
(2) R=280Ω, C=8µF, L=2H,仿真时间: 0.1s
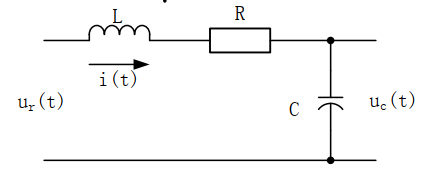
两组参数下电路的单位阶跃响应。 (初始条件均为零)。
2. 熟悉并理解掌握MATLAB模型转换以及参数提取指令(针对上述系统写出它们的运行结果)
G=tf(num,den) G1=tf(G)
G=zpk(z,p,k) G1=zpk(G)
G=ss(A,B,C,D) G3=ss(G)
[num,den]=tfdata(G)
[Z,P,K]=zpkdata(G)
[A,B,C,D]=ssdata(G)
三、实验要求
1. 预习和完成实验内容
2. 完成实验报告,内容至少包括:理论分析,实验程序,程序运行结果以及结果分析。
四、实验内容
1.建模
列方程:
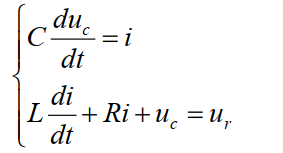
状态空间表达式(时域):
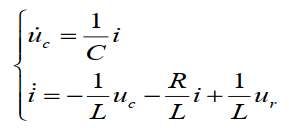
写成矩阵形式:
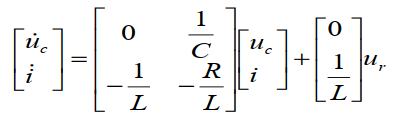
拉氏变换后得传递函数(复域):
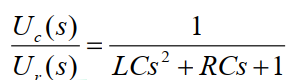
2. 实验代码:
%********** 参数提取 *************
R = 4000;
C = 0.000001;
L = 1;
num = [1];
den = [L*C, R*C, 1];
G = tf(num, den)
G1 = tf(G)
G2 = zpk(G)
G3 = ss(G)
[Num, Den] = tfdata(G)
[Z, P, K] = zpkdata(G)
[A, B, C, D] = ssdata(G)
问题(1):
clear;
clc;
%******************************************%%
% Question 1
%******************************************%%
R1 = 4000;
C1 = 0.000001;
L1 = 1;
A1 = [0, 1/C1;-1/L1,-R1/L1];
B1 = [0;1/L1];
h1 = 0.00003; % step size
y1 = [0;0];
y2 = [0;0];
% ******** Euler method **********%
for i1 = 0:1:1000
t1 = i1*h1; % simulation time: 0.03s
x1(i1+1) = t1;
k1 = A1 * y1 + B1;
k2 = A1 * (y1+h1*k1) + B1;
y1 = y1 + (k1 +k2)*h1/2;
result_for_Euler_1(i1+1) = y1(1,1);
end
% ******** 4 order Runge-Kutta method **********%
for i2 = 0:1:1000
t2 = i2*h1; % simulation time: 0.03s
x2(i2+1) = t2;
k1 = A1 * y2 + B1;
k2 = A1 * (y2+h1*k1/2) + B1;
k3 = A1 * (y2+h1*k2/2) + B1;
k4 = A1 * (y2+h1*k3) + B1;
y2 = y2 + (k1 +k2)*h1/2;
result_for_RK_1(i2+1) = y2(1,1);
end
subplot(2,2,1);plot(x1,result_for_Euler_1,'b');
xlabel(' time /s ');ylabel(' Uc /V ');title('Result for Euler method');legend('Euler');
subplot(2,2,2);plot(x2,result_for_RK_1,'r');
xlabel(' time /s ');ylabel(' Uc /V ');title('Result for Runge-Kutta method');legend('Runge-Kutta');
subplot(2,1,2);plot(x1,result_for_Euler_1,'b', x2,result_for_RK_1,'r');
xlabel(' time /s ');ylabel(' Uc /V ');
title('Comparision of results between Euler and RK');legend('Euler','Runge-Kutta');
问题(2):
clear;
clc;
%******************************************%%
% Question 2
%******************************************%%
R1 = 280;
C1 = 0.000008;
L1 = 2;
A1 = [0, 1/C1;-1/L1,-R1/L1];
B1 = [0;1/L1];
h1 = 0.0002; % step size
y1 = [0;0];
y2 = [0;0];
% ******** Euler method **********%
for i1 = 0:1:500
t1 = i1*h1; % simulation time: 0.1s
x1(i1+1) = t1;
k1 = A1 * y1 + B1;
k2 = A1 * (y1+h1*k1) + B1;
y1 = y1 + (k1 +k2)*h1/2;
result_for_Euler_1(i1+1) = y1(1,1);
end
% ******** 4 order Runge-Kutta method **********%
for i2 = 0:1:500
t2 = i2*h1; % simulation time: 0.1s
x2(i2+1) = t2;
k1 = A1 * y2 + B1;
k2 = A1 * (y2+h1*k1/2) + B1;
k3 = A1 * (y2+h1*k2/2) + B1;
k4 = A1 * (y2+h1*k3) + B1;
y2 = y2 + (k1 +k2)*h1/2;
result_for_RK_1(i2+1) = y2(1,1);
end
subplot(2,2,1);plot(x1,result_for_Euler_1,'b');
xlabel(' time /s ');ylabel(' Uc /V ');title('Result for Euler method');legend('Euler');
subplot(2,2,2);plot(x2,result_for_RK_1,'r');
xlabel(' time /s ');ylabel(' Uc /V ');title('Result for Runge-Kutta method');legend('Runge-Kutta');
subplot(2,1,2);plot(x1,result_for_Euler_1,'b', x2,result_for_RK_1,'r');
xlabel(' time /s ');ylabel(' Uc /V ');
title('Comparision of results between Euler and RK');legend('Euler','Runge-Kutta');
3. 运行结果
问题(1):
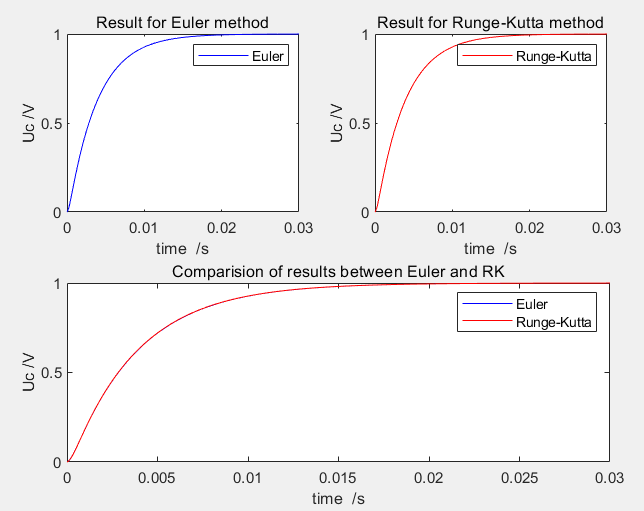
问题(2):
标签:仿真,h1,传函为,A1,B1,y1,y2,Euler,状态方程
来源: https://www.cnblogs.com/KaifengGuan/p/11837496.html
最后
以上就是笑点低鞋子最近收集整理的关于matlab传函转zpk形式,实验一:状态方程、传函为模型的系统的仿真的全部内容,更多相关matlab传函转zpk形式,实验一:状态方程、传函为模型内容请搜索靠谱客的其他文章。








发表评论 取消回复