《数字逻辑设计与计算机组成》一2.6　电路时序图

2.6　电路时序图

在讨论电路时序图之前，我们首先从非门电路时序图开始。每一个逻辑门都有一定的延时。这个延时是由于逻辑门输出从0到1或者反过来一个或多个输入变化需要时间。图2-18展示了非门0.1ns延迟的时序。如图2-18a所示，当输入x从0变为1时，输出z在0.1ns中从1变为0。类似地，当x从1变为0时，在0.1ns中从0变为1。在图2-18a中，信号的转换显示成立即发生。然而，在实际中，信号转换并非立即发生。

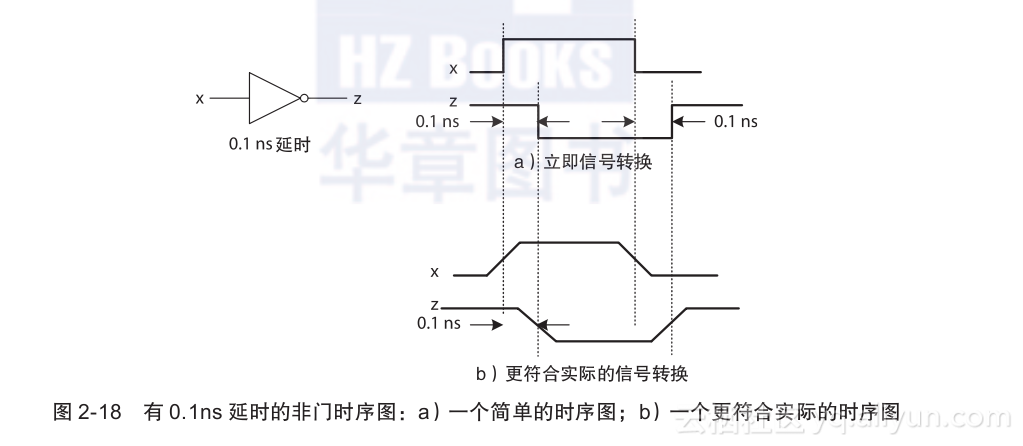
信号上升时间是输出电压从逻辑0的对应值上升到逻辑1的对应值所需的时间。类似的，信号下降时间是输出电压从逻辑1的对应值下降到逻辑0的对应值所需的时间。逻辑门的上升时间和下降时间可能不一样。图2-18b展示了更实际的非门时序电路图，包括其上升时间和下降时间。如图所示，上升和下降的中点通常用于现实信号的立即转换。
对于+ 5.0伏特电压的电源，所有在0～0.8V之间的输入值都被视为逻辑0，所有在2.0～5.0V之间的输入值都被视为逻辑1。一个输入电压大于0.8V且小于2.0V之间的值都被视为未定义的。对于逻辑1输出，电压范围是2.4～5.0V之间，对于逻辑0，对应输出电压范围是0～0.4V之间。更低的电压源（例如，1.8V或者1.2V）通常用于电池供电的系统中。
最小布尔表达式定义了不需要考虑逻辑门和线路延迟的电路输入和输出之间的逻辑关系。一个电路时序图是每个逻辑门的输出在电路中由于逻辑门和电路延迟而发生实际变化的说明图。当电路输入发生变化时，时序图提供了电路行为的一个更实际的视图。例如，考虑表达式f (a, b, c, d) = Σ (1, 3, 5, 7, 10, 11, 14, 15)，其最小SOP表达式为f = d + ac；由此可看出f不由b决定。图2-19展示了与其等价的与非门电路，中间信号为、x和y；逻辑门被标记为G1到G4。
图2-20展示了当输入从acd = 111到acd = 011时电路的时序图；即a从1转变为0。假设所有逻辑门的延迟为0.1ns，线路延迟忽略不计。（线路延迟超出本书范围。）考虑到当输入为acd = 111或者acd = 011时，f = d + ac都会产生f = 1。然而，由于逻辑门存在延迟，f在0.2～0.3ns内不会一直为1，如时序图所示。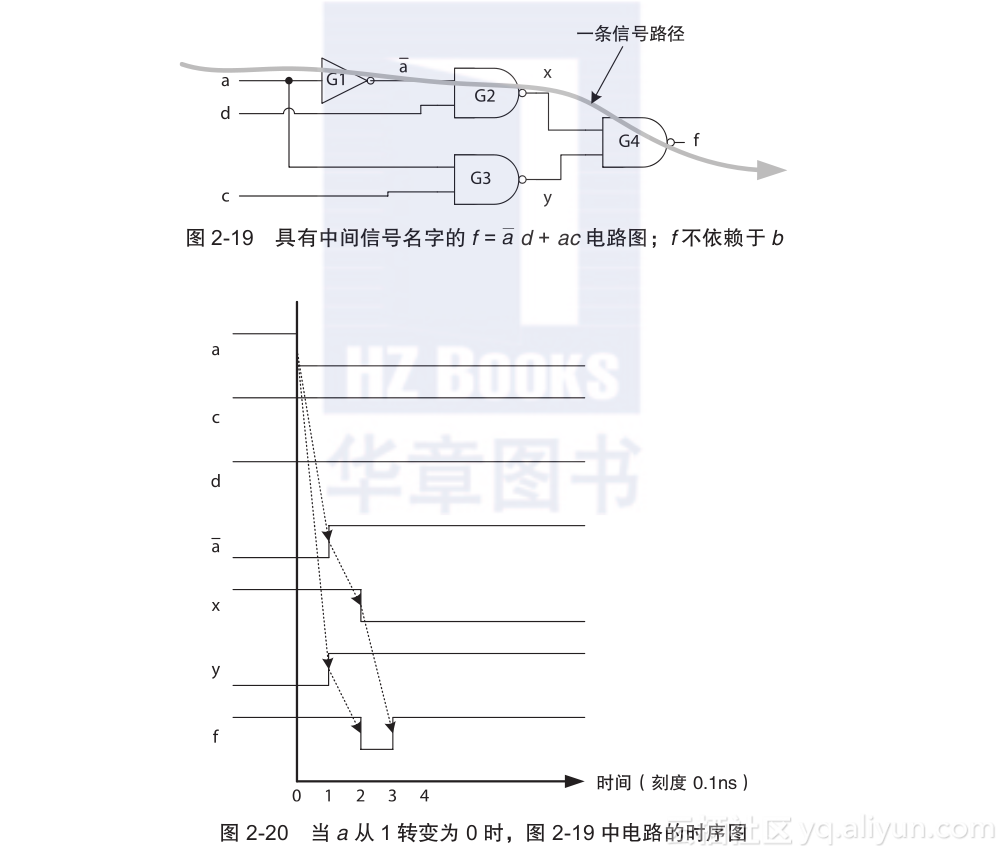

在时间步1中a信号在G1逻辑门中从初始值0到1的改变，使得0.1ns的延迟后从0变为1。当a变成0即变为1时，在图中用箭头表示这种变化。同时，在时间步1中，信号y在G3逻辑门中在0.1ns的延迟后从0变成1。信号在0.1ns时的改变，引起了在逻辑门G2 0.1ns的延迟之后，信号x在时间步2中从1到0的改变。当变为1，x变为0时，在图中用箭头表示这种变化。
在时间= 0.1ns时，信号x和y都为逻辑1，在逻辑门G4 0.1ns延迟后，f从1转变为0。在时间= 0.2ns时，信号x转变成0，时间= 0.3ns时，f在0.1ns后转变为1。此时f一直保持为1。
信号f这种非预期的从1变成0又变为1的变化称为冒险或者电子脉冲，它取决于电路中逻辑门和线路的延迟（此处线路延迟忽略不计）。在这个例子中，当函数f = d + ac输入从acd = 111变为acd = 011时，称其有1-冒险。当一个与或（或者只有或非门）电路的时序图展示了一个从0到1又回到0的非预期的变化，我们就说这个电路有0-冒险。
冒险违背了组合电路的预期行为，且必须要阻止其影响数字系统的状态（例如寄存器内容）。在第4章中，我们将介绍一种有固定期限的时钟信号，一直在1 0 1 0 1 0 1 0…中来回变换，以控制寄存器的加载时间。在图2-20中，输出f在电路输入做出改变之后的0.3ns是合法的。时钟周期取决于信号的传播延迟和其他在第4章和第5章中提到的延迟。

2.6.1　信号传播延迟

通常，在电路中有多条从输入到一个或多个输出的信号路径。例如，图2-19中的输出信号f由信号路径G1-G2-G4或者G3-G4决定。当输入信号改变，传播到输出信号改变所需的时间是由信号路径上的逻辑门的数目和大小及线路延迟决定的。最长路径所产生的延迟称为电路的传输延迟。忽略线路延迟，电路的传输延迟与电路中最长信号路径的逻辑门数量成正比。图2-19中路径G1-G2-G4是最长路径。这样，电路传输延迟和三个逻辑门的延迟成正比，或者为0.3ns，如图2-20所示；这里简单地假设每个逻辑门有0.1ns的延迟。0.3ns的延迟也是消除输出f的1-冒险所需的时间，也是当其电路输入从acd = 111到acd = 011进行转换时，根据其逻辑表达式使得电路的输出f = 1的所需时间。
通常来说，有多个输出电路模型的传输延迟是由从其输入到输出的最长路径决定的。在这个例子中，一些独立的输出可以有短一些的传输延迟；而然，在电路中至少有一个输出信号有最长的路径，这决定了这个电路模型的传输延迟。
实现SOP和POS表达式的电路通常有一些信号路径包含二级逻辑门或者三级逻辑门，包括初始的非门。这将导致传输延迟只与两个或者三个逻辑门延迟成正比。这样SOP或者POS表达式通常通过加快输出速度来提高性能。
然而，包含许多变量逻辑项的表达式可能由于逻辑门的扇入限制（稍后讨论）无法使用二级或者三级电路实现。在这个例子中，一个表达式必须可以分成更小的表达式，每一个表达式用需要更少扇入的逻辑门的更小的电路实现。然后更小的电路连接起来，构成最终的多级电路，不考虑最初的非门。例如，FPGA，作为一个可编程芯片，通常只有有限的资源而无法实现任意大小的SOP或者POS表达式。FPGA通常比高性能的定制芯片要慢。

2.6.2　扇入和扇出

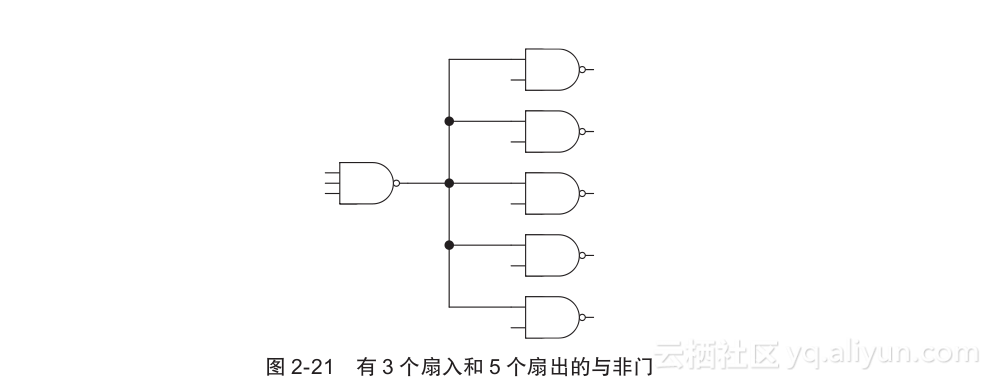
扇入是指一个逻辑门可以拥有的输入个数，扇出是指一个逻辑门可连接输出的连接数。例如，图2-21展示了一个有3个扇入和5个扇出的与非门。一个非门的扇入永远为1。一个异或门和异或非门的扇入通常为2。与门、或门、与非门和或非门的扇入可以为多个；然而，每一个门为了运行正常，都拥有最大扇入和最小扇出限制（例如8）。