粗同步 符号同步 matlab,13.3.4 OFDM系统的同步设计（3）

3．载波同步算法及仿真

发送端和接收端振荡器振荡频率的不匹配性或因为热漂移产生振荡频率的抖动，导致接收中频信号或基带信号的相位与对应的发送信号之间存在相位差，这种相位差与频率差有关。频率偏差越大，相位差也越大。而且这种频差对相差的影响具有累加性，前一个符号的相位差会直接传给后一个符号。本节主要介绍设计系统所采用的频率同步算法及相位补偿算法。

频率同步

根据第13.3.3节的介绍，频率同步可以粗略地分为数据辅助和非数据辅助两大类。在本系统中，使用的是数据辅助的算法。

此处训练序列至少需要包括两个重复的符号。当发送时域数据信号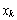 时，重复的通频带等效信号为：

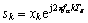
其中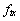， 为发送载波频率。在接收端忽略噪声的情况下，重复的基带等效信号为：

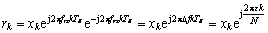
其中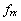， 为接收载波频率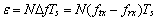， 为归一化载波频率偏差。定义两个连续重复符号之间的延时为 D个采样点，符号长度为L，定义中间变量：

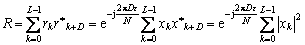
从而得到归一化载波频率偏差的估值为：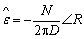 

频偏估计范围为 。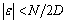

由式13-57可知，频偏的估计范围由N、D来决定。在本系统中，短训练序列中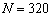 、 、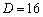 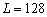，因此频偏估计范围为 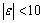(2000Hz)；若取长训练序列，则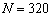、 、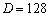 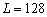，频偏估计范围为250Hz。前一个方法有较大的纠偏范围，但是估计值得到的方差较大；后一个方法的纠偏范围较小，但是得到的方差较小。因此，可以将上述两种方法相结合，应用前导序列的短训练符号作频率粗估计，应用长训练符号作频率细估计，频率跟踪可以用循环前后缀的周期重复性并使用上述方法来完成，其中 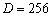、 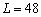，频偏估计范围为125Hz。这样就完成了系统的频率同步。

本系统的频率同步实现结构如图13-23所示。

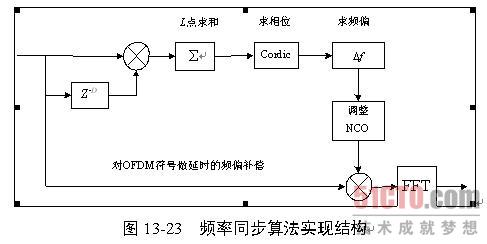
频率粗同步、频率细同步及频率跟踪对应的D、L是不同的，但实际的ASIC设计中可以采用流水线的方式，所以乘法器和累加器只需要一套。可以使用数控震荡器(NCO)来纠正频率偏移，NCO采用CORDIC算法来实现，这样可以简化硬件的复杂程度。

相位补偿

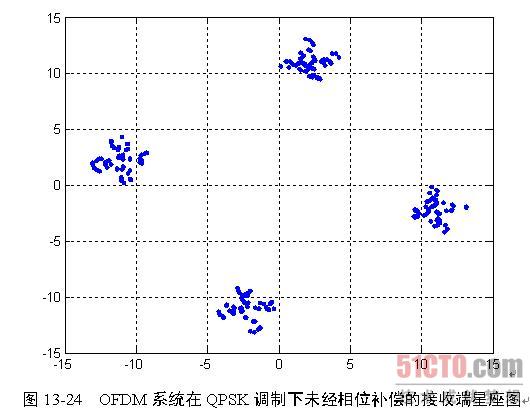
图13-23这个锁频环路只能纠正频率的偏差，不能纠正相位的偏差，图13-24给出了本系统所设计的OFDM系统在QPSK调制方式下且载波频率误差在0.5%以下时，由于相位误差星座图发生偏转的情况。

在频域系统需要导频所提供的信息来做相位补偿，进而消除相位偏差对系统的影响，若记相应的相位偏差为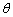 ，那么经过FFT之后可得：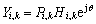

其中 为OFDM的符号数， 为第 个符号的第 个数据， 为导频， 为信道冲击响应。假设接收信道估计结果完全正确，定义中间变量：

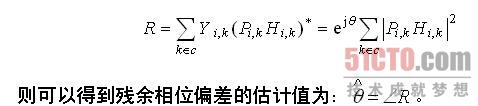
经过相位补偿后，从星座图上来看QPSK调制的数据已经基本上旋转回到星座图上45度的位置，如图13-25所示。

【责任编辑：董书 TEL：(010)68476606】

点赞 0