自动控制原理（2）——系统时域设计

1.比例-微分（PD）控制

（1） 将比例（P）控制改为比例-微分（PD）控制：不改变常值稳态误差，只改善系统动态性能。特点是：自然频率$w_n$不变，阻尼比增大，因为它们与K有关，所以适当选择开环增益K和微分时间常数$T_d$，即可达到目的。比例-微分（PD）控制，相当于给系统增加了一个闭环零点-z=$-1/T_d$。
（2）简要归纳比例-微分（PD）控制对系统性能的影响：
a.增大系统阻尼，使阶跃响应的超调量下降，调节时间缩短，且常值稳态误差和自然频率不变。
b.采用微分控制后，允许选用较大的开环增益K，在保证一定的动态性能条件下，减小稳态误差。

2.MATLAB验证分析

在输入R(s)作用下，闭环传递函数为
$$\frac{K+11S}{S^2+12S+K}$$
在扰动N(s)作用下，闭环传递函数为
$$\frac{-1}{S^2+12S+K}$$
由特征方程结合劳斯判据可知当K大于0时，系统即稳定。但还需要考虑扰动的影响以及动态性能。为了满足要求，需要选择合适的K，这里取K=100和20。

>> K=[100 20];
for i=1:1:2
sys=tf([11 K(i)],[1 12 K(i)]); %建模，R(s)作用下
sysn=tf([-1],[1 12 K(i)]) ;%建模，N(s)作用下
figure(i);t=0:0.002:3;
step(sys,t);hold on;
step(sysn,t);grid
end

结果如下：

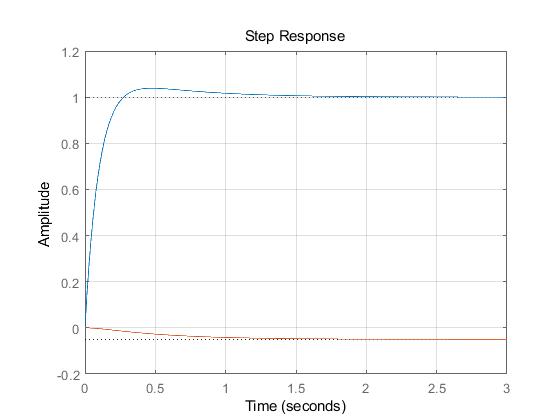
（1）蓝色实线为K=20，输入信号作用下的响应；橙色虚线为K=20，扰动信号作用下的响应
（2）蓝色实线为K=100，输入信号作用下的响应；橙色虚线为K=100，扰动信号作用下的响应
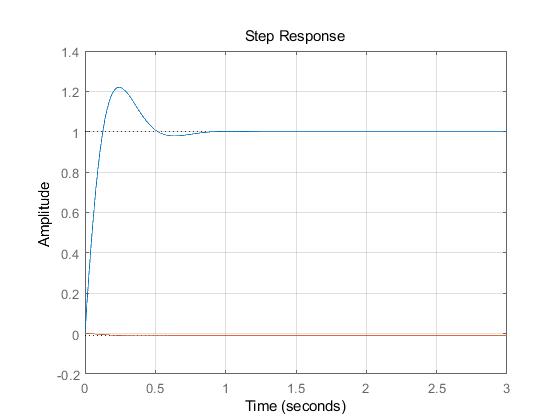该控制系统在两种增益情况下的单位阶跃响应性能如表3-6所示。

因此，应取K=20。

最后

以上就是尊敬月饼为你收集整理的自动控制原理（2）——系统时域设计的全部内容，希望文章能够帮你解决自动控制原理（2）——系统时域设计所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。