时序逻辑电路
给时序逻辑电路下个定义的话,我觉得应该就是当前状态受之前状态和当下状态的影响。
一、锁存器和触发器
1)SR锁存器
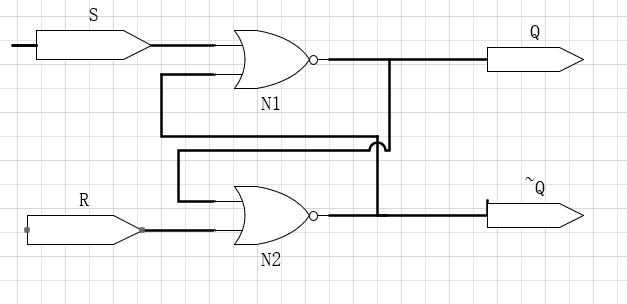
| R | S | Q | ~Q |
|---|---|---|---|
| 0 | 0 | Qprev | ~Qprev |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 |
SR锁存器相当于有四个状态:
- 置位为1,复位为0
- 置位有效,则本位为1
- 置位为0,复位为1
- 复位有效,则本位为0
- 置位为0,复位为0
- 保留先前的值
- 置位为1,复位为1
- 不定输出,混乱电路
特点:
正常情况下通过分别使得SET有效和RESET位有效来传递值(如果二者都有效,则会产生混乱电路,输出不确定),当SET和RESET位都无效时,保存先前值。
2)D锁存器
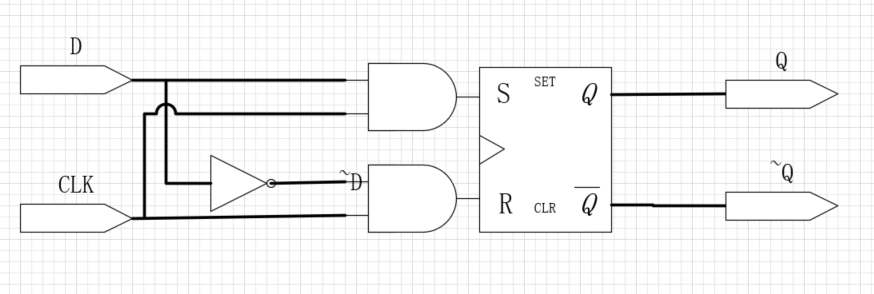
| CLK | D | ~D | S | R | Q | ~Q |
|---|---|---|---|---|---|---|
| 0 | X | ~X | 0 | 0 | Qprev | ~Qprev |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 |
D锁存器有三个状态:
- CLK = 0
- 无论D取什么值,SR都是0,输出Q保持原先的状态
- CLK = 1
- Q的取值和D的取值相同
- D = 0 R = 1
- Q = 0
- D = 1 S =1
- Q = 1
- D = 0 R = 1
- Q的取值和D的取值相同
简单来说:
最大的特点就是时钟有效修改值,时钟无效保持值
好处:
避免出现RS同时有效,出现混合电路的情况。
clk为0,时阻塞数据D通过D锁存器流向Q,此时D锁存器是不透明的。
clk为1,数据D可以流向Q,此时D锁存器是透明的,相当于一个缓冲器
这里称D锁存器为透明锁存器或电平敏感锁存器
3)D触发器
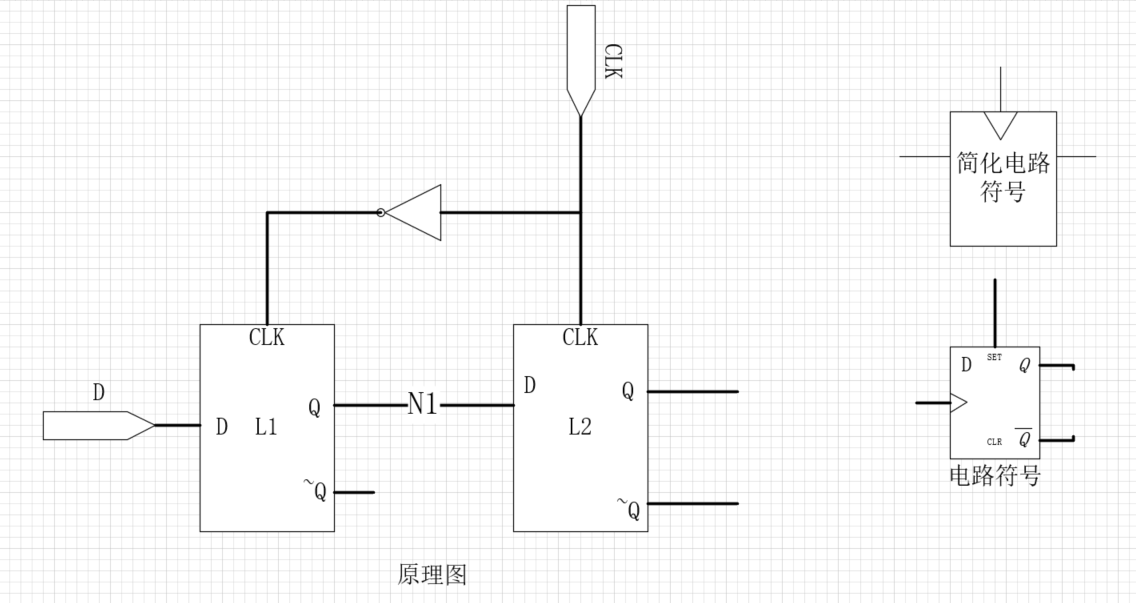
原理:
通过两个D触发器受同一CLK信号控制实现,前一个触发器L1为主锁存器,后一个触发器L2为从触发器。
- 当CLK为0时
- 主触发器为透明,将D数据传递到N1
- 当CLK为1时
- 主触发器阻塞,从触发器透明,将数据复制到Q
保证在一个时钟信号的范围内,从0~1的过程将数据传递给N1,然后当clk到了1就将数据复制给Q,而在其他时刻因为总存在一个触发器处于阻塞的状态,所以保证在其他时刻数据不改变
换句话说就是:
在时钟上升沿将D复制给Q,在其他时间D触发器保持原来的状态。
时钟上升沿常被简称为时钟沿,D触发器的效应就是输入D确定状态,时钟沿确定状态发生改变的时间
D触发器常被成为“主从触发器”,“边沿触发器”,“正边沿触发器”
4)寄存器
原理图:
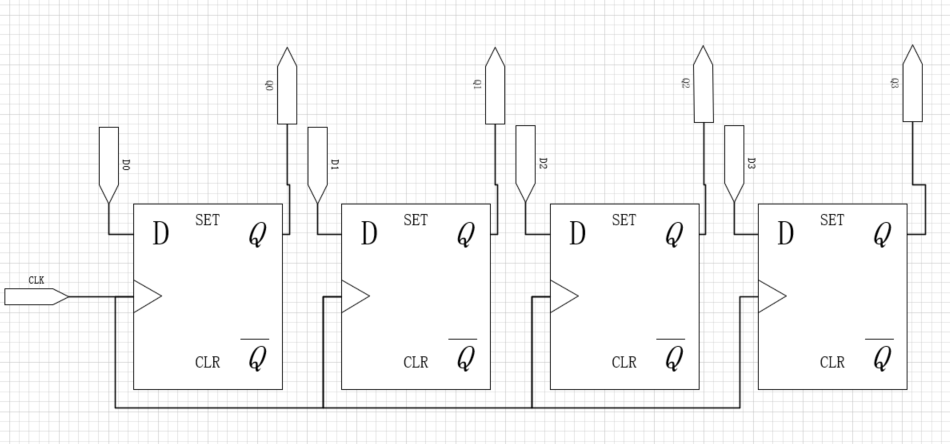
四路输入输出的寄存器电路符号
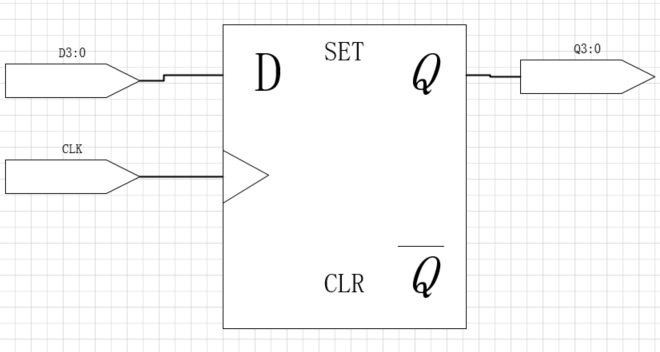
一个N位寄存器往往都是由N个触发器和共享的一个CLK输入组成
也就是说触发器是寄存器的组成单位
5)带使能端的触发器
目前的触发器是否传递数据完全由CLK去决定,可是时钟控制信号是以周期频率来控制的,可以通过设置频率修改周期,但是可控性非常低,所以可以引入使能(EN OR Enable)来提高可控性
即当CLK = 1,且EN =1 时,才能传递数据,保证了虽然时钟周期上升沿到了,但是仍然不想传递数据问题的解决,很大程度上提高了可控性。
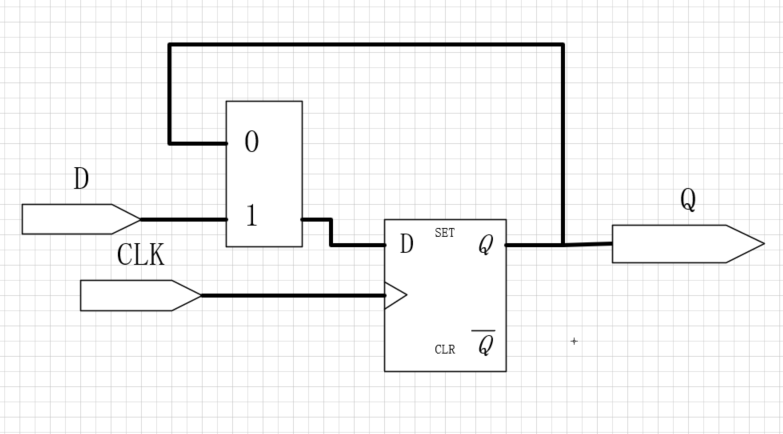
实现带使能端的触发器有两种实现方式:
-
通过多路选择器控制
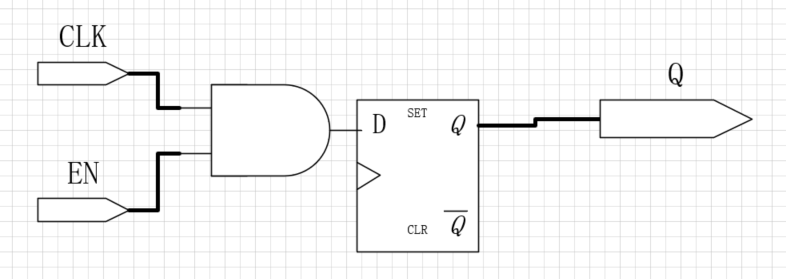
-
门控
6)带复位功能的触发器
为D触发器添加~RESET输入,如果RESET为False,则带复位的D触发器和普通D触发器一样,当RESET = TRUE,则带复位功能的触发器忽略D并将输出Q复位为0。
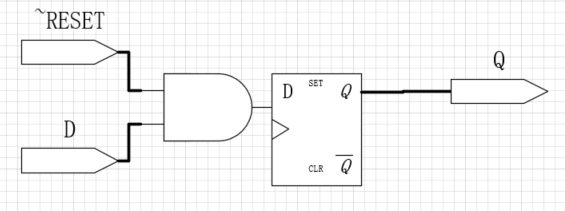
上图是RESET复位信号低电平有效时的原理图,下图则是RESET复位信号高电平有效时的原理图,其实只需要一个非门(反相器)就能实现高电平有效。
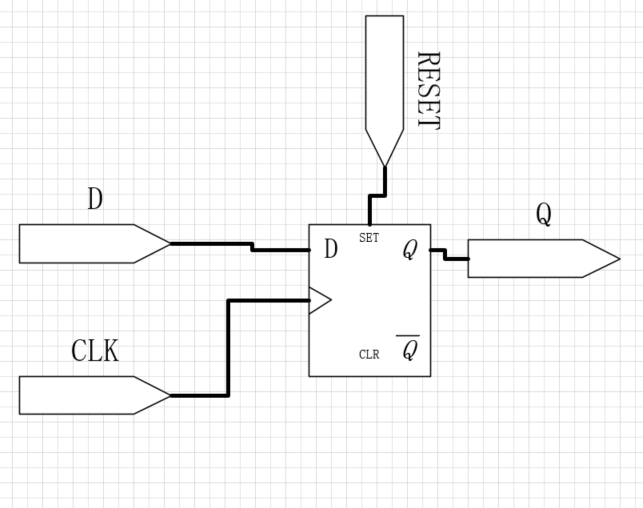
一般的,复位功能触发器分为两种,1)同步复位,只有当CLK = 1时才能完成复位功能。
2)异步复位,只要RESET设置为True 就可以完成立即完成复位功能,不受时钟信号的限制
7)触发器和锁存器比较
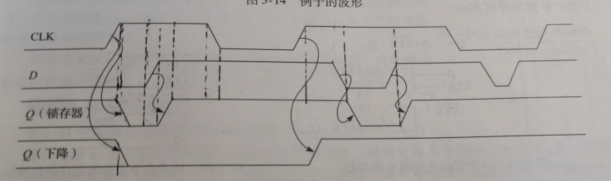
从图上可以看到,D锁存器没当逢时钟信号为1,且D变化时,Q的值变化
D触发器,仅当CLK处于时钟上升沿时,且同时D变化,才会变化,其余都保持原值。
且变化都是从时钟信号上升沿结束开始的,因为无论是什么样的电路都有一定的延迟。在一开始处于平行线是因为在波形开始的时候Q的初值是未知的,且只有彻底踩到上升沿的时候才会开始变化。
8)小结
对于基本的时序逻辑电路来说,主要需要将一开始的SR锁存器的原理弄清楚,后面的D锁存器和D触发器的原理就一目了然了。
简化时序逻辑应该从内容和时间触发。
丰富时序逻辑的本质就是让时序逻辑电路的可控性提高吗,比如说添加使能端,比如说添加复位信号。
锁存器组成触发器,触发器组成寄存器,多个寄存器实现完整的时序逻辑。
二、同步逻辑设计
学习目的:
了解时序逻辑电路的概念和动态约束,重点讨论同步时序电路,找到一种简单、系统的方法来设计和分析时序电路系统。
1)一些有问题的电路
非稳态
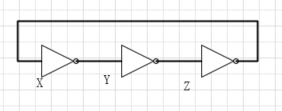
| X | Y | Z |
|---|---|---|
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 0 |
观察电路和真值表都可以发现,在第一次数据传递过程中,反馈给X的数据是1,但是这与X是0的一开始的假设不一致。则这样一次通路中反馈与假设不同的情况称这个电路没有问题的的状态,称为不稳定态或非稳态
但是对于X的值来说,需要两次通路就会有一次循环,然后这个模式会一直的持续重复下去,如果假设一个反相器有1ns的延迟,那么每个结点(x or y or z)在0~1之间摆动,这个电路称为环形振荡器
环形振荡器的周期取决于每个反相器的传播延迟,而这个延迟不好计算,因为他取决于反相器的制造工艺,电源电压甚至工作温度。
所以环形振荡器的基本特点就是:
- 非稳态
- 零输入
- 周期性改变输出的时序电路
竞争条件:
一句话描述:
因为门的使用存在延迟,再加上们郁闷的延迟时间不同,那么在使用异步时序电路就会因为这些延迟影响电路的行为(影响电路行为就是说:最后电路的逻辑不仅收到本身逻辑门之间组成关系的影响,还受到延迟路径的影响)
详细定义:
由于电平异步时序电路各反馈的延迟时间不同,如果电路在状态转移过程中存在两个或两个以上的状态同时改变,那么就会产生状态改变的先后,这种现象称为反馈回路间的竞争。
竞争分两类,如果竞争不影响逻辑结果,则称竞争为非临界竞争,如果产生了错误的状态转移,影响了逻辑结果,就称为临界状态。
消除竞争的方式:一般处理这样反馈回路里面的竞争问题,设计师一般在回路路径中添加寄存器来断开环路,让电路变成组合逻辑电路和寄存器的集合。如果时钟足够慢,下一个时钟信号到达之前,输入到寄存器的值,都可以稳定下来,所有竞争都会被消除。
2)同步时序电路
1、概述
定义电路的方法:
一般从电路的输入输出端,功能规范和时序规范就可以定义一个电路,而一个时序电路往往有一组有限的离散状态{S0,S1,…Sk-1}
一般用当前状态和下一状态 区分目前系统的状态,和下一个时钟上升沿系统将进入的状态
功能规范:说明了当前状态和输入值的各种组合,每个输出的下一个和值
时序规范:包括上界时间tpcq 和 下界时间teaq 是从时钟上升沿到输出改变事件以及建立时间tsetup,保持时间thold。
需要注意的是:表示输入必须相对于时钟上升沿稳定
根据这些规范确定了时序同步电路的组成原则:
- 时序同步电路的元件组成只能是寄存器或者组合电路
- 只要要有一个电路元件是寄存器
- 所有寄存器都接收同一个时钟信号
- 每个环路至少包含一个寄存器
示例:
对于一个寄存器来说本身就是一个最简单的时序逻辑电路:
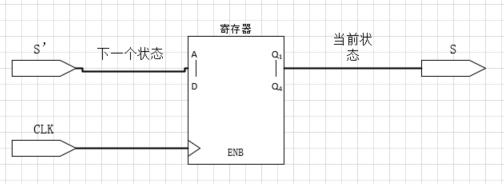
一般用S’表示下一个状态,用S表示当前状态。
最常见的同步时序电路称为有限状态机和流水线
2、有限状态机
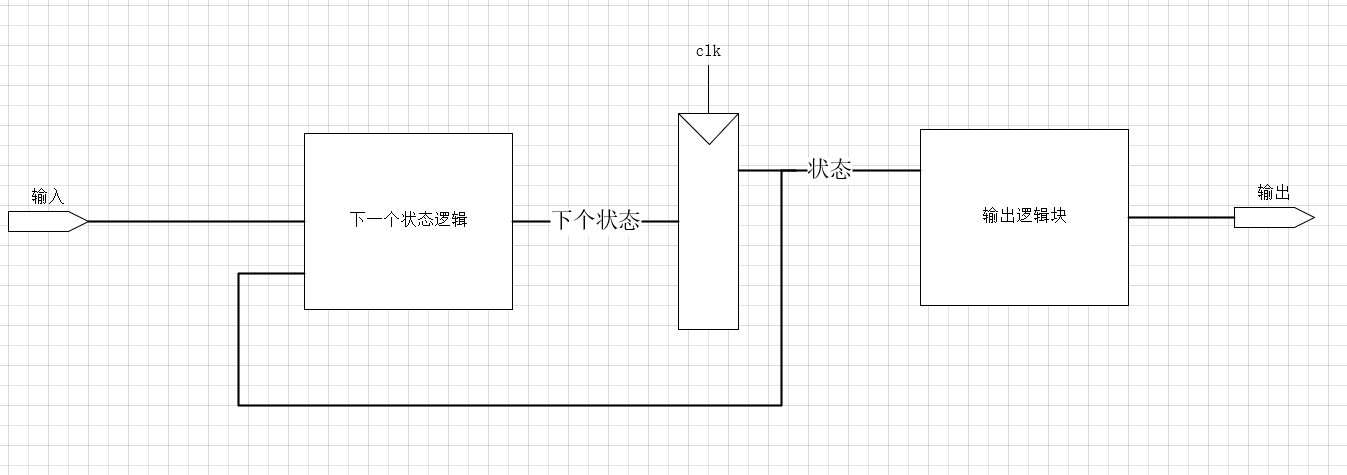
同步时序电路描绘成图示的样子就称为有限状态机(Finite State Machine,FSM),从名字上来说就是因为具有K位寄存器的电路可以处于2^k种状态种的某一种唯一状态。
M位的输入,N位的输出,再加上K位的状态,再加上具有一个时钟信号和可选的复位型号,就组成了有限状态机。
而有限状态机一般包含两个组合逻辑块:
- 下一个状态逻辑块(next state logic)
- 输出逻辑块(output logic)
- 用于存储状态的寄存器
有限状态机根据功能描述分为两种:
- Moore型状态机
- 输出仅取决于当前状态
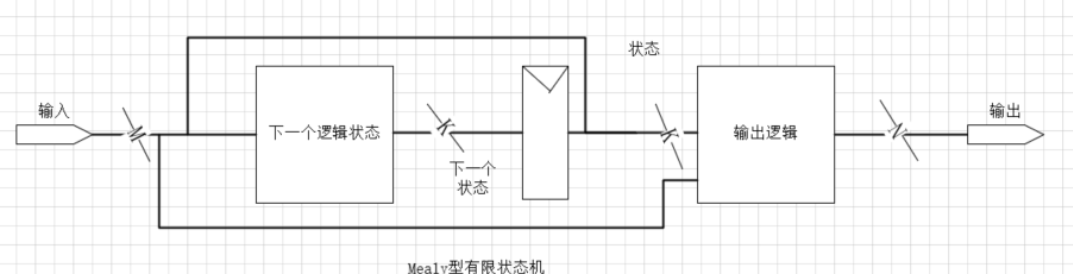
- Mealy型状态机
- 输出由当前状态和当前输入共同决定
3、设计一个含有限状态机的通路
a、要求


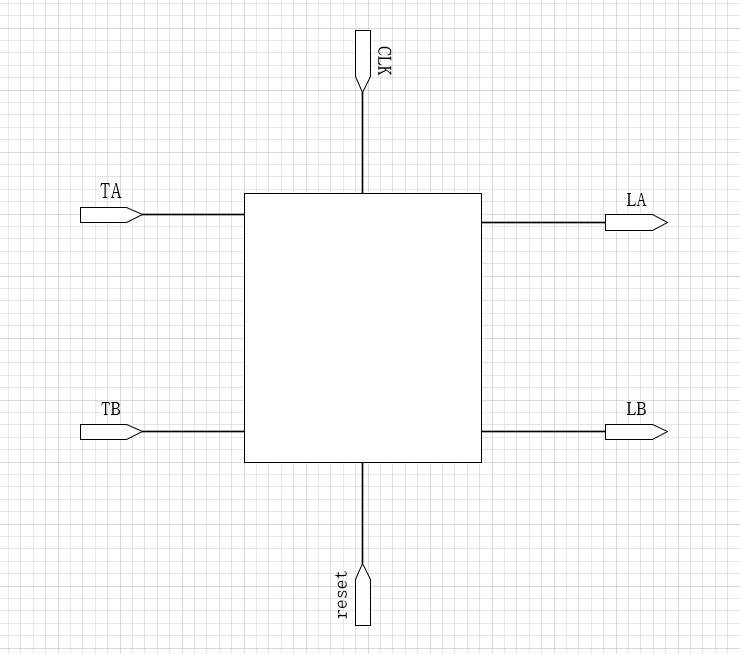
b、设计黑盒视图
黑盒视图就是包含所有输入输出的模块视图,在设计时序逻辑电路甚至任何电路的时候也一样,先设计出顶层模型。
c、考虑实现逻辑
#1、画出状态转换图
状态转换图是描述各种状态之间转换关系的视图,需要注意以下几个内容:
- 圆圈代表状态,圆弧代表两种状态间的转换
- 状态转换只发生在时钟的上升沿,所以只根据状态转换图中的位置来判断是什么时候发生了状态转换
- reset 信号有效意味着无论当前的状态是什么状态都会进入S0状态
- 如果一个状态有多个离开他的弧,那么这些弧上标有触发每个状态的条件
- Ta = True ,则保持当前S0状态
- Ta = False ,则转换为S1状态
- 如果只有一个离开他的弧,不管输入是什么,当时钟上升沿的时候,转换一定会发生
- 状态S1一定会转换向状态S2
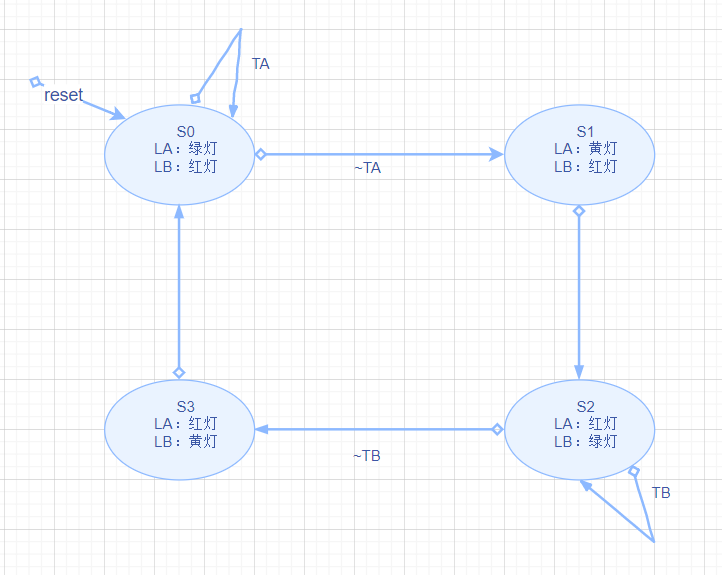
只要LA所在的Academic 大道上有交通,则LA就恒为绿灯,当且只当,Academic大道上没有交通时,则一定会转向S1状态,S1和S3都无法长期保持,都会在下一个时钟周期进行转换。
#2、根据图画出状态转换表
- 状态转换表会说明每个状态和输入值,以及应该产生的下一个状态是什么
- 无关项X表示,下一个状态的产生不依赖这个的输入
- 省略了复位信号,但可以使用任何带复位信号的触发器复位后进入S0,这样就不用考虑任何输入
| 当前状态 | TA | TB | 下一个状态S’ |
|---|---|---|---|
| S0 | 0 | X | S1 |
| S0 | 1 | X | S0 |
| S1 | X | X | S2 |
| S2 | X | 0 | S3 |
| S2 | X | 1 | S2 |
| S3 | X | X | S0 |
#3、实现状态编码
为了可以实现电路,必须将所有的状态,输出进行编码
| 状态编码表 | |
|---|---|
| S0 | 00 |
| S1 | 01 |
| S2 | 10 |
| S3 | 11 |
| 输出编码表 | |
|---|---|
| 绿灯 | 00 |
| 黄灯 | 01 |
| 红灯 | 10 |
wire S[1:0];
wire LA1[1:0];
wire LA2[10]
通过状态编码表来改进状态转换表,进而写出下一个状态S’的真值表
| 当前状态 | 输入 | 下一个状态 | |||
|---|---|---|---|---|---|
| S1 | S0 | TA | TB | S1’ | S0’ |
| 0 | 0 | 0 | X | 0 | 1 |
| 0 | 0 | 1 | X | 0 | 0 |
| 0 | 1 | X | X | 1 | 0 |
| 1 | 0 | X | 0 | 1 | 1 |
| 1 | 0 | X | 1 | 1 | 0 |
| 1 | 1 | X | X | 0 | 0 |
#4、得到布尔表达式
根据真值表可以直接写出布尔表达式
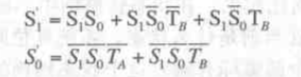
这两个表达式可以通过卡诺图去花间也可以通过观察法化简:
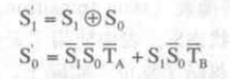
然后可以根据每一个状态去写出的输出的逻辑表(因为设计的是Moore型的状态机,输出仅取决于当前状态,所以可以直接写出输出):
| 当前状态 | 输出 | ||||
|---|---|---|---|---|---|
| S1 | S0 | LA1 | LA0 | LB1 | LB0 |
| 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 |
根据逻辑表写出输出的布尔表达式:
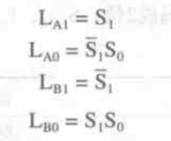
#5、根据表达式设计电路
首先可以根据设计的状态和输入的关系来设计出下一个状态逻辑块的电路:
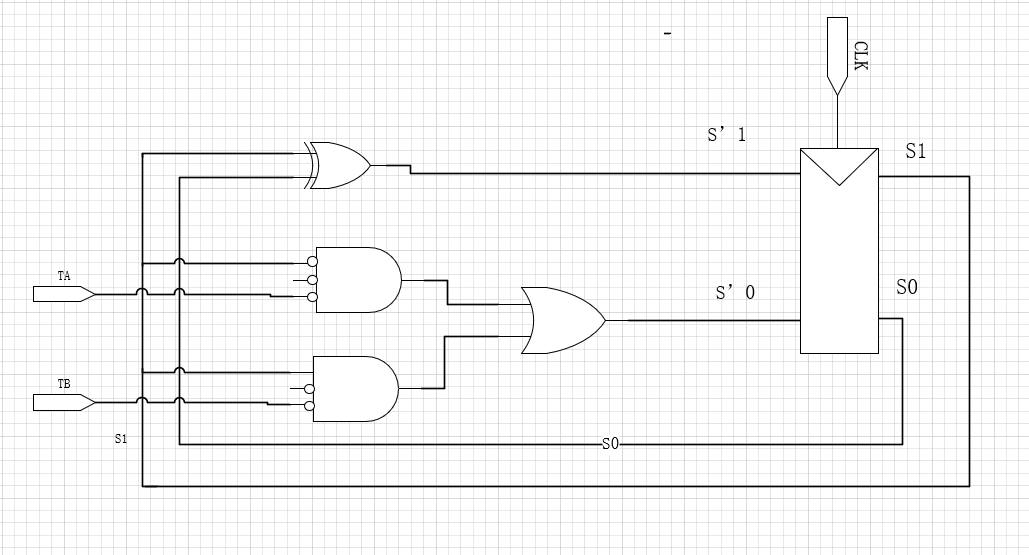
再根据输出的布尔表达式来得到含输出的电路:
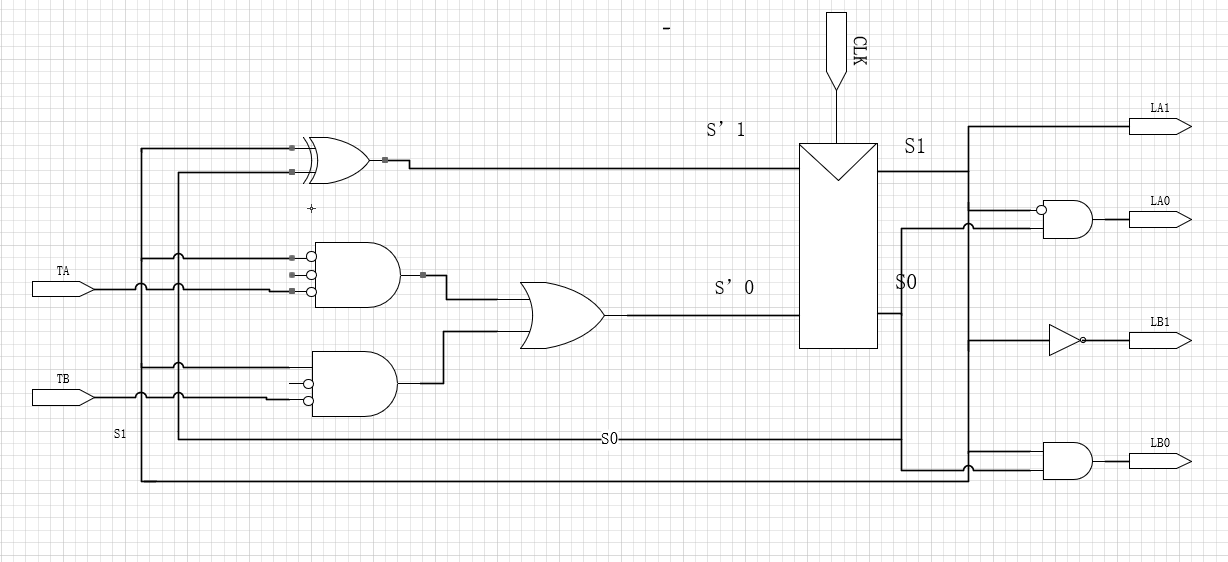
4、状态编码
在上面的例子中通过确定状态编码来产生不同的输出电路,那么如何确定和约定一个状态编码就是一个最直接的问题。好的状态编码能使逻辑门的使用最少,而且传换的延迟最短。但是目前并没有一种办法能找出最好的状态编码,除了尝试所有可能的情况,但状态数据很大的时候比如说32位或者64位的时候,这样的方式很显然是不可以的。通过观察相关状态或输出共享某些位以便于选择一种合适的编码方式(可以使用计算机CAD工具来帮助)
常见的状态编码有两种:
- 二进制编码:
- 一共有log2k种状态
- 独热码:
- 需要更多的触发器,使用独热码往往下一个状态逻辑和输出逻辑比较简单(门电路更少),最佳的编码方式取决于具体的有限状态机。
最后
以上就是跳跃橘子最近收集整理的关于我的西皮优学习笔记(二)->时序逻辑电路时序逻辑电路的全部内容,更多相关我内容请搜索靠谱客的其他文章。








发表评论 取消回复