全文共8090个字，码字总结不易，老铁们来个三连：点赞、关注、评论
作者：[左手の明天]
 原创不易，转载请联系作者并注明出处
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

“优化”是生活中经常使用的词：坐出租车时希望司机不绕弯路、走优化路线；逛超市时考虑各种优惠活动，希望获得最大优惠；企业推出新产品要综合考虑成本与市场吸引力，对资金进行优化配置，等等。 这些问题都是“最优化问题”，也是数学建模中的典型问题，解决最优化问题的数学方法就是“最优化方法”。

最优化方法的出发点是系统思维，最优化方法的基本思路是在一定的约束条件下，保证各方面资源的合理分配， 最大限度地提升系统某一性能或系统整体性能，最终实现最理想结果。运用最优化方法建立并求解数学模型，主要包括以下步骤：

（1）明确目标，分析问题背景，确定约束条件，搜集全面的客观数据和信息；
（2）建立数学模型，构建变量之间的数学关系，设立目标函数；
（3）分析数学模型，综合选择最适合该模型的优化方法；
（4）求解模型，通常借助计算机和数学分析软件完成；
（5）对最优解进行检验和实施。

目录

数学规划的一般模型

MATLAB 求解优化问题的主要函数

模型及基本函数

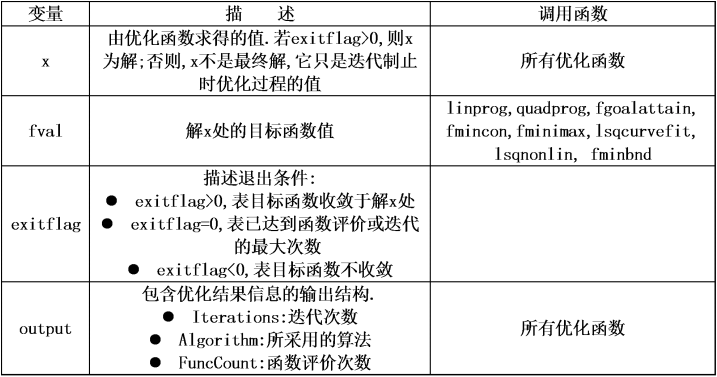
优化函数的输入变量

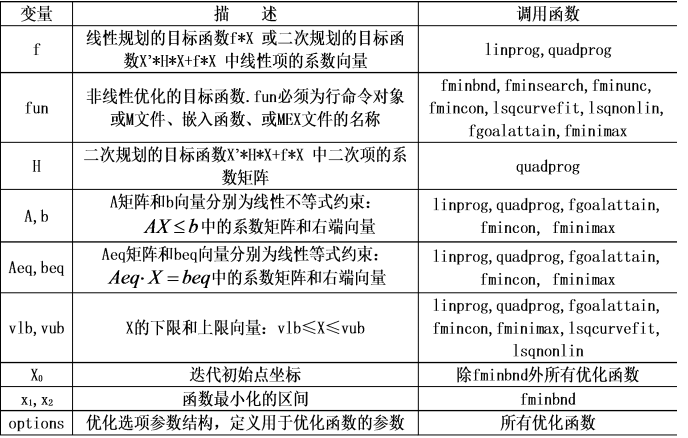
优化函数的输出变量

无约束最优化问题

数学描述

解析解法和图解法

数值解法

全局最优解和局部最优解

带约束最优化问题

线性规划问题

情况一

情况二

二次规划问题

非线性规划问题

定义

求解算法1：间接法

求解算法2：直接法

求解算法3：最速下降法（steepest descent method）

Matlab求解步骤

示例

0-1规划问题

钢管的订购与运输问题

问题

问题1的基本模型和解法

总费用最小的优化问题

基本模型：二次规划

Floyd算法求解步骤 

最优化方法在数学建模中的应用 

梯度下降法

惩罚函数法

遗传算法

蚁群算法

---

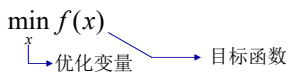
数学规划的一般模型

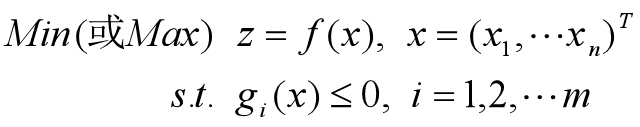
其中，x~决策变量；f(x)~目标函数；gi(x)≤0~约束条件

---

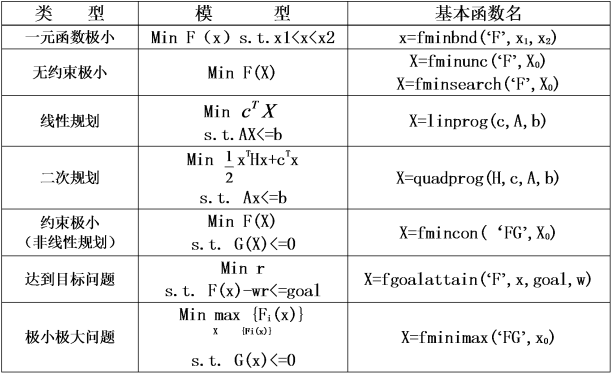
MATLAB 求解优化问题的主要函数

模型及基本函数

优化函数的输入变量

优化函数的输出变量

---

无约束最优化问题

数学描述

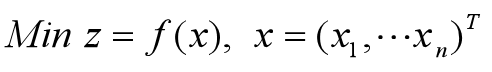
解析解法和图解法

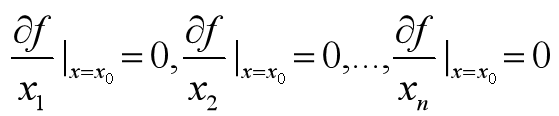
 举例：用解析和图解法求解下列方程

<<syms t; 
y=exp(-3*t)*sin(4*t+2)+4*exp(-0.5*t)*cos(2*t)-0.5;
ezplot(y,[0 4])
y1=diff(y);
ezplot(y1,[0 4])
t0=solve(y1)
y2=diff(y1);
b=subs(y2,t,t0)

数值解法

 命令形式1：

x=fminsearch(fun,x0)   %简单形式

[x,f,flag,out]=fminsearch(fun,x0,opt,p1,p2,…) %一般形式

功能：与fsolve()中的参数控制形式类似。

注：若函数时多元的，要表达成向量的形式。

命令形式2：

x=fminunc(fun,x0)   %简单形式

[x,f,flag,out]=fminunc(fun,x0,opt,p1,p2,…) %一般形式

功能：与fsolve()中的参数控制形式类似。

举例：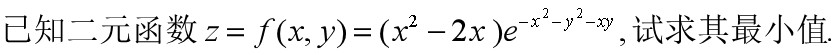

>>f=inline('(x(1)^2-2*x(1))*exp(-x(1)^2-x(2)^2-x(1)*x(2))','x');
x0=[0,0];
ff=optimset;ff.Display='iter';
x=fminsearch(f,x0,ff)

>>x=fminunc(f,x0,ff)

全局最优解和局部最优解

一元函数极小

X=fminbnd(fun,x1,x2)

多元无约束极小

X=fminunc(fun,x0) (牛顿法)
X=fminsearch(fun,x0)

举例1：(初值的影响力)设目标函数为

 试观察不同的初值得出的最小值。

>> f=inline('exp(-2*t)*cos(10*t)+exp(-3*(t+2))*sin(2*t)','t');
t0=1;[t1,f1]=fminsearch(f,t0)

t1=0.92275390625000,f1=-0.15473299821860

>> t0=0.1;[t2,f2]=fminsearch(f,t0)

t2=0.29445312500000,f2=-0.54362463738706


>> syms t; 
y=exp(-2*t)*cos(10*t)+exp(-3*(t+2))*sin(2*t);
ezplot(y,[0,2.5]); axis([0 2.5 -0.6 1])

举例2：对边长为3米的正方形铁板，在四个角剪去相等的正方形以制成方形无盖水槽，问如何剪法使水槽的容积最大？

建立模型： 

设剪去的正方形的边长为x,，则水槽的容积为：

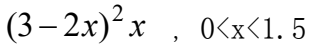
建立无约束优化模型为：

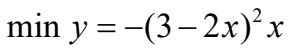
模型求解：

先编写M文件如下:

function f=myfun(x)
f=-(3-2*x).^2*x;

调用fminbnd:

[x,fval]=fminbnd(@myfun,0,1.5)

运算结果为：

x = 0.5000,fyal =2.0000.

即剪掉的正方形的边长为0.5米时水槽的容积最大，最大容积为2立方米。

---

带约束最优化问题

线性规划问题

目标函数：

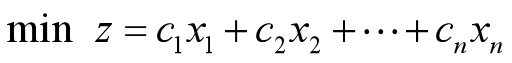
 约束条件：

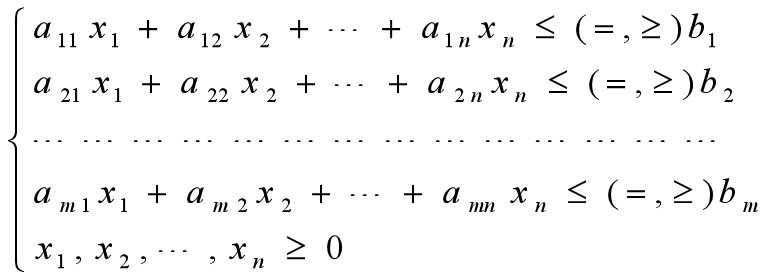
情况一

目标函数：

其中，C为价值向量

约束条件：

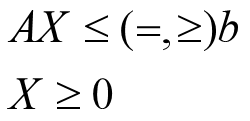
 其中，b为资源向量；X为决策变量向量

其中：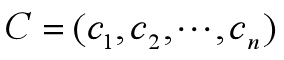

 

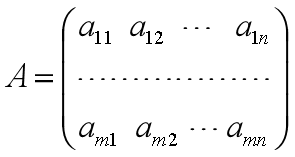
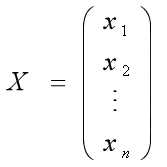
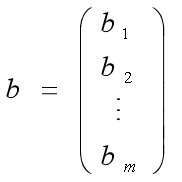
命令形式1：

[X,lag,how]=lp(C,A,b,v1,v2,x0)

功能：

• C,A,b的意义如矩阵表示里参数；
• v1,v2表示决策变量的上界和下界（其维数可以小于X,但表示前几个分量的上下界）；
• x0表示初始值；X时输出最优解；
• lag是lagrange乘子，维数等于约束条件的个数，非零的向量是起作用的约束条件；
• how给出错误信息：infeasible(无可行解)，unbounded(无界解)，ok(求解成功).

 举例：

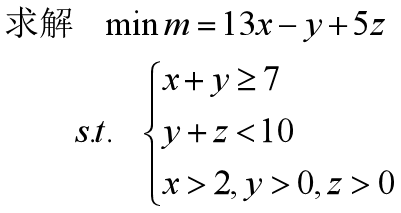
>> c=[13,-1,5];
A=[-1,-1,0;0,1,1];
b=[-7,10];
v0=[2,0,0];
[X,lag,how]=lp(c,A,b,v0)

情况二

目标函数：

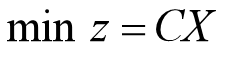
 约束条件：

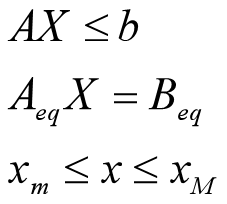
命令形式2：  

[X,f,flag,c]=linprog(C,A,b,Aeq,Beq,xm,xM,x0,opt)

功能：各个参数的解释如前，若各个约束条件不存在，则用空矩阵来代替。

• x: 解
• f: 最优值
• flag：大于零表示求解成功，否则求解出问题
• c：求解信息
• x0：搜索点的初值
• opt：最优化控制项

举例1：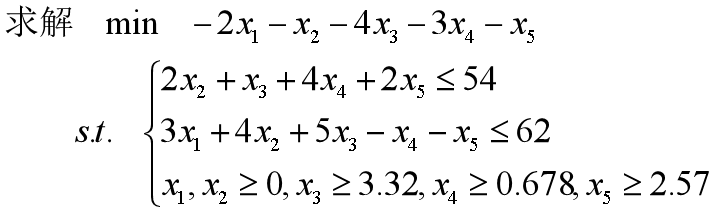

>> c=[-2,-1,-4,-3,-1];
 A=[0 2 1 4 2;3 4 5 -1 -1];
 b=[54,62];
 Ae=[];Be=[];
 xm=[0,0,3.32,0.678,2.57];
 ff=optimset;
 ff.LargeScale='off';
 ff.TolX=1e-15;
 ff.Display='iter';
 [X,f,flag,c]=linprog(c,A,b,Ae,Be,xm,[],[],ff)

举例2：某车间生产A和B两种产品，为了生产A和B，所需的原料分别为2个和3个单位，所需的工时分别为4个和2个单位。现在可以应用的原料为100个单位，工时为120个单位。每生产一台A和B分别可获得利润6元和4元。应当生产A和B各多少台能获得最大利润？

分析：

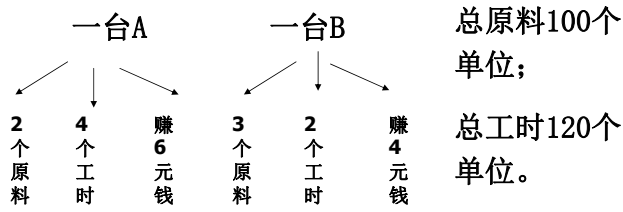
 模型建立：

设生产A产品x1 台，生产B产品 x2台

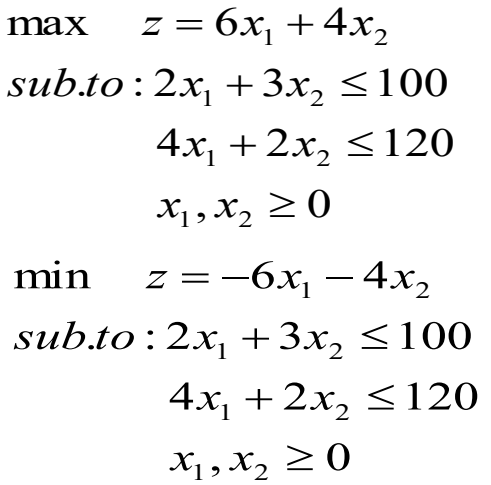
 模型求解：

f=[-6,-4]';
A=[2 3;4 2];
B=[100;120];
Ae=[];
Be=[];
xm=[0,0];
ff=optimset;
ff.LargeScale='off'; % 不用大规模问题求解
ff.TolX=1e-15;
ff.TolFun=1e-20; 
ff.TolCon=1e-20;
ff.Display='iter';
[x,f_opt,key,c]=linprog(f,A,B,Ae,Be,xm,[],[],ff)

举例3：（任务分配问题）某车间有甲、乙两台机床，可用于加工三种工件。假定这两台车床的可用台时数分别为 800 和 900，三种工件的数量分别为 400、600 和 500，且已知用三种不同车床加工单位数量不同工件所需的台时数和加工费用如下表。问怎样分配车床的加工任务，才能既满足加工工件的要求，又使加工费用最低？

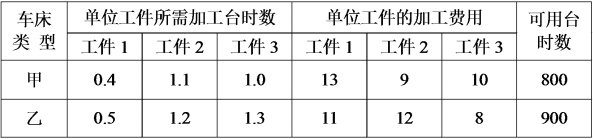
模型建立：

设在甲车床上加工工件 1、2、3 的数量分别为 x1、x2、x3，在乙车床上加工工件 1、2、3 的数量分别为 x4、x5、x6。可建立以下线性规划模型：

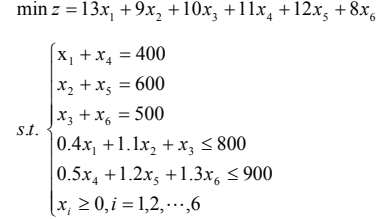
模型求解：

f = [13 9 10 11 12 8];
A = [0.4 1.1 1 0 0 0
0 0 0 0.5 1.2 1.3];b = [800; 900];
Aeq=[1 0 0 1 0 0
0 1 0 0 1 0
0 0 1 0 0 1];
beq=[400 600 500];
vlb = zeros(6,1);
vub=[];
[x,fval] = linprog(f,A,b,Aeq,beq,vlb,vub)

举例4：某厂每日 8 小时的产量不低于 1800 件。为了进行质量控制，计划聘请两种不同水平的检验员。一级检验员的标准为：速度 25 件/小时，正确率 98%，计时工资 4 元/小时；二级检验员的标准为：速度 15 小时/件，正确率 95%，计时工资 3 元/小时。检验员每错检一次，工厂要损失 2 元。为使总检验费用最省，该工厂应聘一级、二级检验员各几名？

模型建立：

设需要一级和二级检验员的人数分别为 x1、x2 人，则应付检验员的工资为：

 因检验员错检而造成的损失为：

故目标函数为：

约束条件为：

 

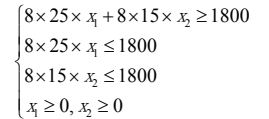
 线性规划模型：

 

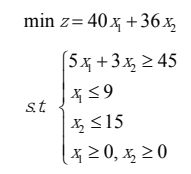
 模型求解：

c = [40;36];
A=[-5 -3];
b=[-45];
Aeq=[];
beq=[];
vlb = zeros(2,1);
vub=[9;15];
%调用 linprog 函数：
[x,fval] = linprog(c,A,b,Aeq,beq,vlb,vub)

结果：

x =
9.0000
0.0000
fval =360

即只需聘用 9 个一级检验员。

二次规划问题

目标函数：

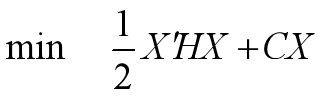
约束条件： 

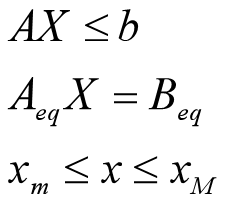
命令形式：

 [X,f,flag,c]=quadprog(H,C,A,b,Aeq,Beq,xm,xM,x0,opt)

功能：

各个参数的解释如前，若各个约束条件不存在，则用空矩阵来代替。

举例：

 

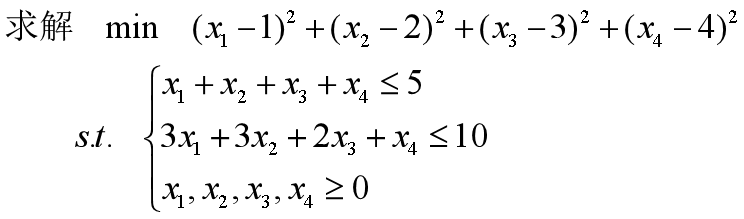
>> c=[-2,-1,-4,-3,-1];
  A=[0 2 1 4 2;3 4 5 -1 -1];
  b=[54,62];
  Ae=[];Be=[];
  xm=[0,0,3.32,0.678,2.57];
  ff=optimset;
  ff.LargeScale='off';
  ff.TolX=1e-15;
  ff.Display='iter';
  [X,f,flag,c]=linprog(c,A,b,Ae,Be,xm,[],[],ff)

非线性规划问题

定义

如果目标函数或约束条件中至少有一个是非线性函数时的最优化问题就叫做非线性规划问题．

一般形式：

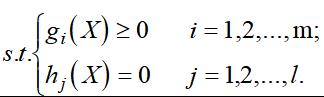
 其中

 

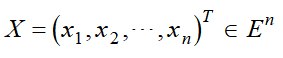
 是定义在 En 上的实值函数，简记:

 

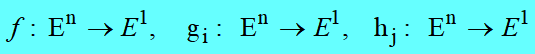
其它情况：

求目标函数的最大值或约束条件为小于等于零的情况，都可通过取其相反数化为上述一般形式．

 

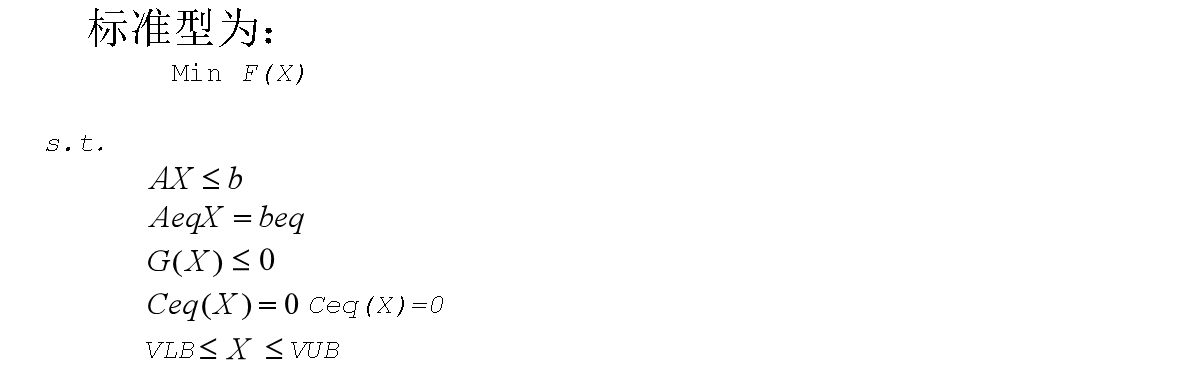
其中X为n维变元向量，G(X)与Ceq(X)均为非线性函数组成的向量，其它变量的含义与线性规划、二次规划中相同.

求解算法1：间接法

在非线性最优化问题当中，如果目标函数能以解析函数表示，可行域由不等式约束确定，则可以利用目标函数和可行域的已知性质，在理论上推导出目标函数为最优值的必要条件，这种方法就称为间接法（也称为解析法） 。 一般要用到目标函数的导数。

求解算法2：直接法

直接法是一种数值方法。这种方法的基本思想是迭代，通过迭代产生一个点序列{ X(k) }，使之逐步接近最优点。 只用到目标函数。 如黄金分割法、Fibonacci、随机搜索法。

迭代法一般步骤

 注意：数值求解最优化问题的计算效率取决于确定搜索方向P (k)和步长的效率。

求解算法3：最速下降法（steepest descent method）

由法国数学家Cauchy于1847年首先提出。在每次迭代中，沿最速下降方向（负梯度方向）进行搜索，每步沿负梯度方向取最优步长，因此这种方法称为最优梯度法。

特点：

方法简单，只以一阶梯度的信息确定下一步的搜索方向，收敛速度慢； 越是接近极值点，收敛越慢； 它是其它许多无约束、有约束最优化方法的基础。 该法一般用于最优化开始的几步搜索。

最速下降法算法：

Matlab求解步骤

用Matlab求解上述问题，基本步骤分三步：

1. 首先建立M文件fun.m,定义目标函数F（X）:

function f=fun(X); 
f=F(X);

 3. 建立主程序.非线性规划求解的函数是fmincon，命令的基本格式如下：       

(1) x=fmincon(‘fun’,X0,A,b)    

(2) x=fmincon(‘fun’,X0,A,b,Aeq,beq)    

(3) x=fmincon(‘fun’,X0,A,b, Aeq,beq,VLB,VUB)          

(4) x=fmincon(‘fun’,X0,A,b,Aeq,beq,VLB,VUB,’nonlcon’)

(5) x=fmincon(‘fun’,X0,A,b,Aeq,beq,VLB,VUB,’nonlcon’,options)

(6) [x,fval]= fmincon(...)

(7) [x,fval,exitflag]= fmincon(...)  

(8) [x,fval,exitflag,output]= fmincon(...)

输入参数的几点说明：

模型中如果没有A,b,Aeq,beq,VLB,VUB的限制，则以空矩阵[ ]作为参数传入；

nonlcon：如果包含非线性等式或不等式约束，则将这些函数编写一个Matlab函数

nonlcon就是定义这些函数的程序文件名；

不等式约束  G(x)<=0

等式约束     Ceq(x)=0.

如果nonlcon=‘mycon’ ; 则myfun.m定义如下

function [G,Ceq] = mycon(x)

G= ... % 计算非线性不等式约束在点x处的函数值

Ceq= ... %计算机非线性等式约束在点x处的函数值 

示例

例子1：

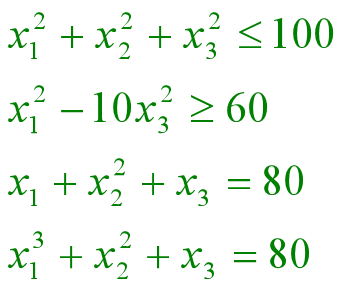
2个不等式约束， 2个等式约束 3个决策变量x1，x2，x3 如果nonlcon以‘test’作为参数值，则程序test.m如下

function [G,Ceq]=test(x)
G(1)=x(1)*x(1)+x(2)*x(2)+x(3)*x(3)-100
G(2)=60-x(1)*x(1)+10*x(3)*x(3)
Ceq(1)=x(1)+x(2)*x(2)+x(3)- 80
Ceq(2)=x(1)^3+x(2)*x(2)+x(3)- 80

注意：

[1] fmincon函数提供了大型优化算法和中型优化算法。默认时，若在fun函数中提供了梯度（options参数的GradObj设置为’on’），并且只有上下界存在或只有等式约束，fmincon函数将选择大型算法。当既有等式约束又有梯度约束时，使用中型算法。

[2] fmincon函数可能会给出局部最优解，这与初值X0的选取有关。

例子2：

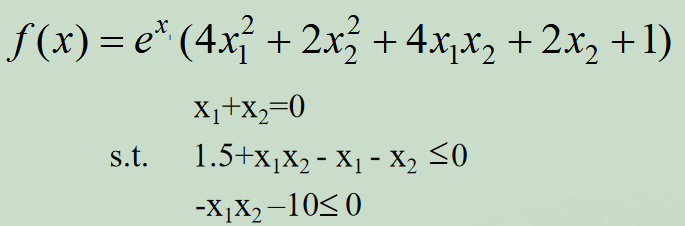
 1．先建立M文件 fun.m,定义目标函数：

function f=fun(x);

f=exp(x(1)) *(4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+2*x(2)+1);

 2．再建立M文件mycon.m定义非线性约束：

function [g,ceq]=mycon(x)

g=[1.5+x(1)*x(2)-x(1)-x(2);-x(1)*x(2)-10];

ceq=[];

3．主程序为：

x0=[-1;1];
A=[];b=[];
Aeq=[1 1];
beq=0; 
vlb=[];
vub=[];
[x,fval]=fmincon('fun4',x0,A,b,Aeq,beq,vlb,vub,'mycon')

4．运算结果为：

x = -1.2250    1.2250        

fval = 1.8951

0-1规划问题

数学描述：自变量的取值只能为0或1

matlab解：

X=bintprog(f,A,B,Aeq,Beq)

小规模问题可以穷举

举例：求解下面的0-1线性规划问题

 

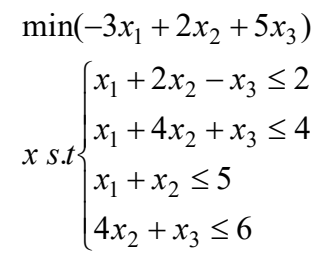
f=[-3,2,-5]; A=[1 2 -1; 1 4 1; 1 1 0; 0 4 1]; 
B=[2;4;5;6];
x=bintprog(f,A,B,[],[])'

---

钢管的订购与运输问题

要铺设一条A1→A2 →……→ A15的输送天然气的主管道，如图一所示(见下页)。经筛选后可以生产这种主管道钢管的钢厂有 。图中粗线表示铁路，单细线表示公路，双细线表示要铺设的管道(假设沿管道或者原来有公路，或者建有施工公路)，圆圈表示火车站，每段铁路、公路和管道旁的阿拉伯数字表示里程(单位km)。

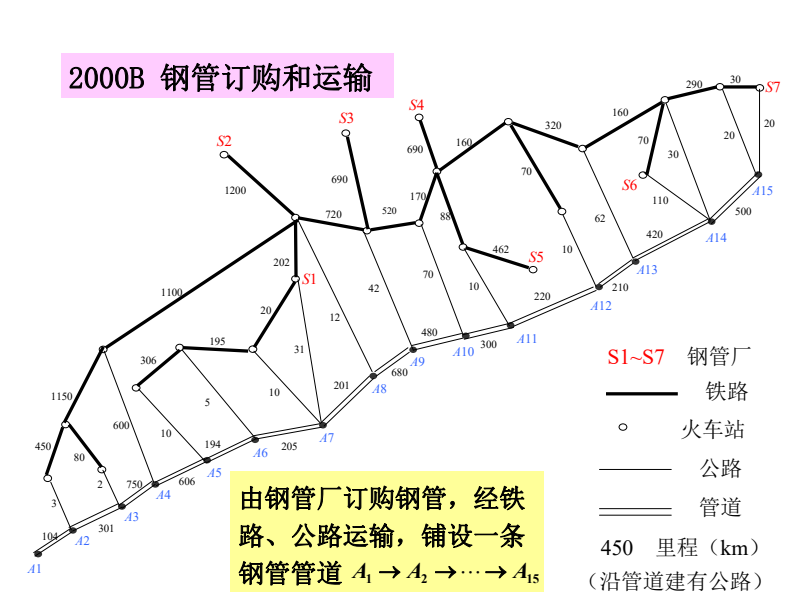
为方便计，1km主管道钢管称为1单位钢管。一个钢厂如果承担制造这种钢管，至少需要生产
500个单位。钢厂Si在指定期限内能生产该钢管的最大数量为Si个单位，钢管出厂销价1单位钢管为pi万元，如下表：

 1单位钢管的铁路运价如下表：

 

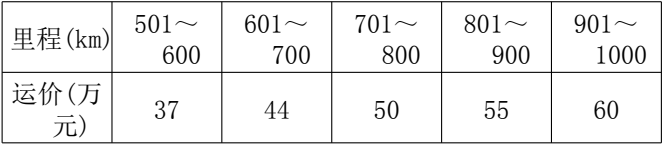
1000km以上每增加1至100km运价增加5万元。公路运输费用为1单位钢管每公里0.1万元（不足
整公里部分按整公里计算）。钢管可由铁路、公路运往铺设地点（不只是运到点A1，A2，……，A15 ，而是管道全线）。

问题

（1）制定钢管的订购和运输计划，使总费用最小.
（2）分析对购运计划和总费用影响：哪个钢厂钢管销价的变化影响最大；哪个钢厂钢管产量上限的变化影响最大？
（3）讨论管道为树形图的情形

问题1的基本模型和解法

总费用最小的优化问题

 

基本模型：二次规划

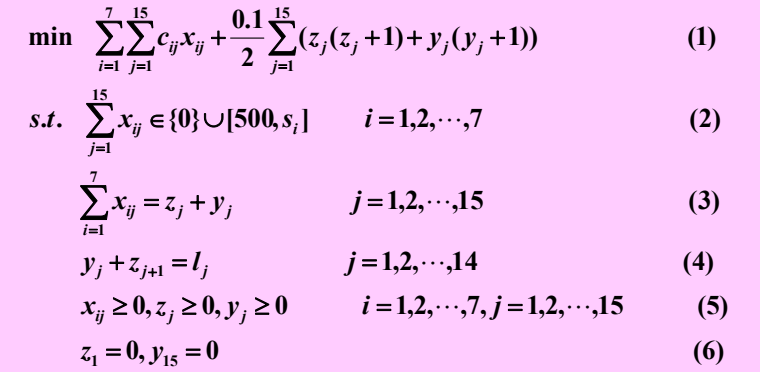
Floyd算法求解步骤 

 Floyd算法过程描述如下：

• １、 首先Ｓ以边集Ｍ初始化，得到所有的直接连通代价；
• ２、 依次考虑第k个结点，对于Ｓ中的每一个Ｓ[i][j]，判断是否满足：S[i][j]>S[i][k]+S[k][j]，如果满足则用S[i][k]+S[k][j]代替Ｓ[i][j]，此为第k步；
• ３、 k循环取遍所有结点，算法结束时，Ｓ为最终解。

 

---

最优化方法在数学建模中的应用 

梯度下降法

梯度下降法是经典的最优化方法之一[4]，其核心思想是高等数学中的导数理论。 梯度下降法实现最优化的原理是，每次迭代更新目标函数时，都以该变量导数（即梯度）的反方向作为更新参数的方向，最终解一定会收敛于最优解。 这个原理类似于走下坡路时，总是沿着最陡峭的方向向下走，最后就一定会走到坡底。梯度下降法的实现简单， 但是求解计算时间长，因此基于梯度下降法发展了很多改进算法，包括随机梯度下降法、小批量梯度下降法等，能够有效改善计算成本高的问题。

惩罚函数法

惩罚函数法，指的是引入惩罚因子和惩罚函数的最优化方法[5]。 具体来说，惩罚函数的思想是：将最优化问题中的约束条件视为围墙，而迭代更新的解视为在围墙内运动的粒子，一旦粒子靠近围墙，对应的惩罚因子数值就会增大，导致惩罚函数值增大，反之，粒子远离围墙时，惩罚函数值就减小。 建立了这种惩罚机制后，在每次迭代过程中，模型为了“避免被惩罚”，逐渐趋近于约束边界，从而找到了最优解。惩罚函数法对模型的训练虽然“简单粗暴”，但是原理直观、实现门槛低，是实际工程中备受青睐的最
优化方法。

遗传算法

不同于梯度下降法和惩罚函数法，遗传算法并非依据导数理论提出的算法[6]，而是一种模拟生物在自然届中进化规律的一种智能算法。 自然界的生物进化遵循适者生存和优胜劣汰，即能够适应环境变化或基因变异的个体才能够参与到进化。 遗传算法的优化原理与之类似：每一次迭代时，通过计算各个个体的适应度，从中随机地选择两个个体作为父母，繁殖后代，同时诱发子代的染色体变异，重复迭代，当出现最大适应度的子代时，即认为获得了最优解，循环结束。与梯度下降法、惩罚函数法相比，遗传算法以生物进化为原型，收敛性较好，在计算精度要求时，具有计算时间少、鲁棒性高的优势。

蚁群算法

与遗传算法类似，蚁群算法也是受启发于生物的一种最优化方法[7]。 生物科学家发现蚂蚁经过的路上都会有一种特殊物质，并且蚁群中的蚂蚁对该物质高度敏感，由于该物质浓度越高，代表着路途长度越短，想要走“捷径”的蚁群们都会选择浓度较高的道路行走，“捷径”经过的蚂蚁越多，特殊物质的浓度就越高，物质浓度积累到一定程度，所有蚂蚁都会被吸引到最佳捷径上来，都能以最快速度找到食物了。 蚁群算法解决最优化问题，就是利用了其分布计算和信息正反馈的特点。

最后

以上就是糟糕裙子为你收集整理的数学建模之优化模型详解数学规划的一般模型MATLAB 求解优化问题的主要函数无约束最优化问题带约束最优化问题钢管的订购与运输问题最优化方法在数学建模中的应用 的全部内容，希望文章能够帮你解决数学建模之优化模型详解数学规划的一般模型MATLAB 求解优化问题的主要函数无约束最优化问题带约束最优化问题钢管的订购与运输问题最优化方法在数学建模中的应用 所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。