优化算法详解

   对于几乎所有机器学习算法，最后一般都归结为求解最优化问题。因此，最优化方法在机器学习算法的推导与实现中占据中心地位。模型优化算法的选择直接关系到最终模型的性能。有时候效果不好，未必是特征的问题或者模型设计的问题，很可能就是优化算法的问题。
   在这篇文章中，将对机器学习中所使用的优化算法做一个全面的总结，并理清它们直接的脉络关系，帮你从全局的高度来理解这一部分知识。

1、机器学习要求解的数学模型

   几乎所有的机器学习算法最后都归结为求一个目标函数的极值，即最优化问题。
(1)对于有监督学习
   我们要找到一个最佳的映射函数f(x)，使得对训练样本的损失函数最小化（最小化经验风险或结构风险）：
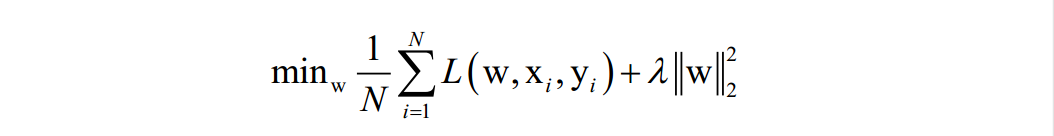   N为训练样本数，L是对单个样本的损失函数，w是要求解的模型参数，是映射函数的参数，xi为样本的特征向量，yi 为样本的标签值。
   或是找到一个最优的概率密度函数p(x)，使得对训练样本的对数似然函数极大化（最大似然估计）：
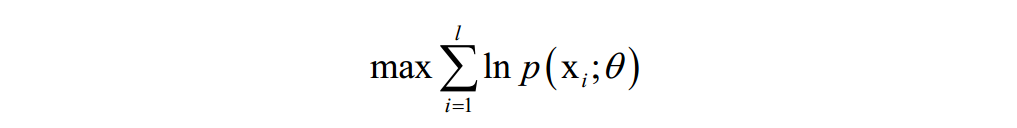   在这里，θ是要求解的模型参数，是概率密度函数的参数。
(2) 1.2对于无监督学习
   以聚类算法为例，算法要是的每个类的样本离类中心的距离之和最小化：
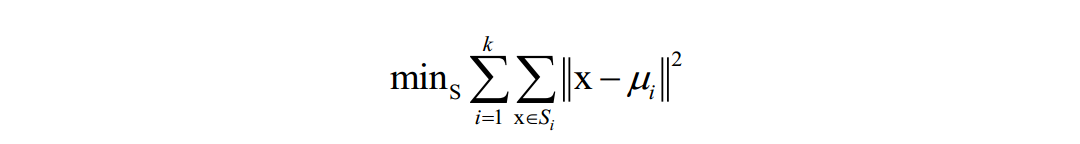   在这里k为类型数，x为样本向量，ui为类中心向量，Si为第i个类的样本集合。
   总体来看，机器学习的核心目标是给出一个模型（一般是映射函数），然后定义对这个模型好坏的评价函数（目标函数），求解目标函数的极大值或者极小值，以确定模型的参数，从而得到我们想要的模型。在这三个关键步骤中，前两个是机器学习要研究的问题，建立数学模型。第三个问题是纯数学问题，即最优化方法，为本文所讲述的核心。

2、最优化算法

2.1 分类

   对于形式和特点各异的机器学习算法优化目标函数，我们找到了适合它们的各种求解算法。除了极少数问题可以用暴力搜索来得到最优解之外，我们将机器学习中使用的优化算法分成三种类型：
   （1）公式解：给出一个最优化问题精确的公式解，也称为解析解，一般是理论结果。
   （2）数值优化：是在要给出极值点的精确计算公式非常困难的情况下，用数值计算方法近似求解得到最优点。
   （3）启发式优化：主要有如：遗传算法，模拟退火，粒子群算法等。除此外还有其他一些求解思想，如分治法，动态规划等。不需要聚合函数，也不需要导数信息。
   （4）除此外还有其他一些求解思想，如分治法，动态规划等。
   下图给出了除（3）外这些算法的分类与它们之间的关系

2.2 通用的优化框架

   掌握了这个框架，可以设计自己的优化算法。各种玄乎其玄的优化算法在步骤3、4都是一致的，主要的差别就体现在1和2上。

3 公式解

3.1 费马定理

   对于一个可导函数，寻找其极值的统一做法是寻找导数为0的点，即费马定理。微积分中的这一定理指出，对于可导函数，在极值点处导数必定为0：

   对于多元函数，则是梯度为0：

   导数为0的点称为驻点。需要注意的是，导数为0只是函数取得极值的必要条件而不是充分条件，它只是疑似极值点。是不是极值，是极大值还是极小值，还需要看更高阶导数。对于一元函数，假设x是驻点：
   1.如果 [公式] (x)＞0，则在该点处去极小值
   2.如果 [公式] (x)＜0，则在该点处去极大值
   3.如果 [公式] (x)＝0，还要看更高阶导数
对于多元函数，假设x是驻点：
   1.如果Hessian矩阵正定，函数在该点有极小值
   2.如果Hessian矩阵负定，函数在该点有极大值
   3.如果Hessian矩阵不定，则不是极值点
   在导数为0的点处，函数可能不取极值，这称为鞍点
   除鞍点外，最优化算法可能还会遇到另外一个问题：局部极值问题，即一个驻点是极值点，但不是全局极值。如果我们对最优化问题加以限定，可以有效的避免这两种问题。典型的是凸优化，它要求优化变量的可行域是凸集，目标函数是凸函数。
   虽然驻点只是函数取得极值的必要条件而不是充分条件，但如果我们找到了驻点，再判断和筛选它们是不是极值点，比之前要容易多了。无论是理论结果，还是数值优化算法，一般都以找驻点作为找极值点的目标。对于一元函数，先求导数，然后解导数为0的方程即可找到所有驻点。对于多元函数，对各个自变量求偏导数，令它们为0，解方程组，即可达到所有驻点。这都是微积分中所讲授的基础方法。幸运的是，在机器学习中，很多目标函数都是可导的，因此我们可以使用这套方法。

3.2 拉格朗日乘数法

   费马定理给出的不带约束条件下的函数极值的必要条件。对于一些实际应用问题，一般还带有等式或者不等式约束条件。对于带等式约束的极值问题，经典的解决方案是拉格朗日乘数法。
对于如下问题：

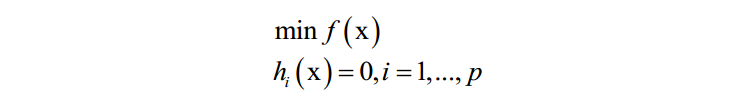
构造拉格朗日乘子函数

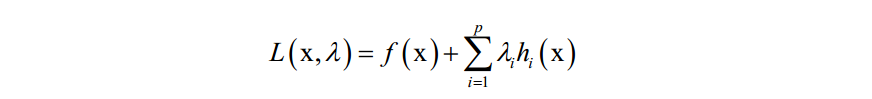
在最优点处对x和乘子变量λi的导数都必须为0：

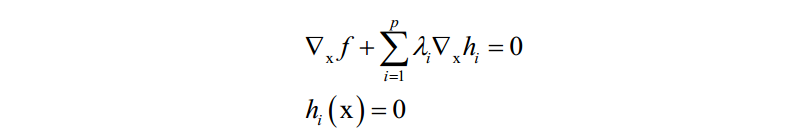
   解这个方程即可得到最优解。对拉格朗日乘数法更详细的讲解可以阅读任何一本高等数学教材。机器学习中用到拉格朗日乘数法的地方有：
   主成分分析
   线性判别分析
   流形学习中的拉普拉斯特征映射
   隐马尔可夫模型

3.3 KKT条件

   KKT条件是拉格朗日乘数法的推广，用于求解既带有等式约束，又带有不等式约束的函数极值。对于如下优化问题：

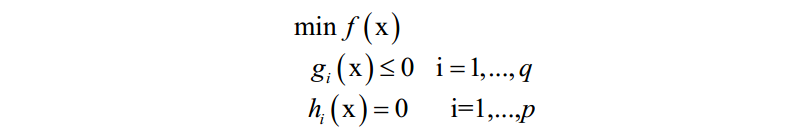
   和拉格朗日对偶的做法类似，KKT条件构如下乘子函数：

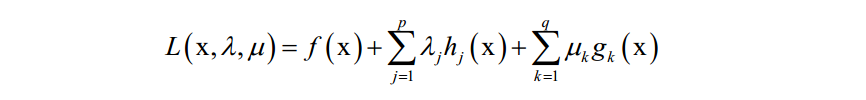
   λ和 u 称为KKT乘子。在最优解处 [公式] 应该满足如下条件：
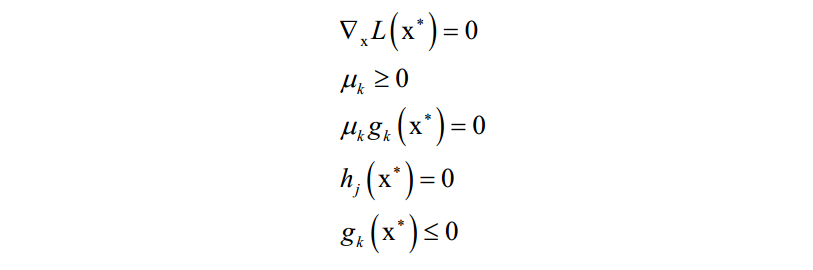   等式约束和不等式约束是本该满足的条件，唯一多了关于gi(x)的条件：

   KKT条件只是取得极值的必要条件而不是充分条件。在机器学习中用到KKT条件的地方有：支持向量机（SVM）

4 数值优化算法

   前面讲述的三种方法在理论推导、某些可以得到方程组的求根公式的情况（如线性函数，正态分布的最大似然估计）中可以使用，但对绝大多数函数来说，梯度等于0的方程组是没法直接解出来的，如方程里面含有指数函数、对数函数之类的超越函数。对于这种无法直接求解的方程组，我们只能采用近似的算法来求解，即数值优化算法。这些数值优化算法一般都利用了目标函数的导数信息，如一阶导数和二阶导数。如果采用一阶导数，则称为一阶优化算法。如果使用了二阶导数，则称为二阶优化算法。
   工程上实现时通常采用的是迭代法，它从一个初始点 x0 开始，反复使用某种规则从 xk移动到下一个点 xk+1 ，构造这样一个数列，直到收敛到梯度为0的点处。即有下面的极限成立：

   这些规则一般会利用一阶导数信息即梯度；或者二阶导数信息即Hessian矩阵。这样迭代法的核心是得到这样的由上一个点确定下一个点的迭代公式：

4.1 梯度下降法

   梯度下降法沿着梯度的反方向进行搜索，利用了函数的一阶导数信息。梯度下降法的迭代公式为：

   根据函数的一阶泰勒展开，在负梯度方向，函数值是下降的。只要学习率 y 设置的足够小，并且没有到达梯度为0的点处，每次迭代时函数值一定会下降。需要设置学习率为一个非常小的正数的原因是要保证迭代之后的 xk+1 位于迭代之前的值xk 的邻域内，从而可以忽略泰勒展开中的高次项，保证迭代时函数值下降。
   梯度下降法及其变种在机器学习中应用广泛，尤其是在深度学习中。

4.1.1 SGD、BGD、MBGD随机梯度下降法

   假设训练样本集有N个样本，有监督学习算法训练时优化的目标是这个数据集上的平均损失函数：

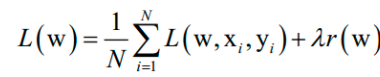
   其中L(w, xi , yi )是对单个训练样本( xi , yi )的损失函数，w是需要学习的参数，r(w)是正则化项，λ是正则化项的权重。在训练样本数很大时，如果训练时每次迭代都用所有样本，计算成本太高，作为改进可以在每次迭代时选取一批样本M≤N，将损失函数定义在这些样本上，近似计算损失函数。随机梯度下降法在概率意义下收敛。
   BGD批量随机梯度下降：是最原始的形式，它是指在每一次迭代时使用所有样本来进行梯度的更新。
   SGD随机梯度下降：不同于批量梯度下降，随机梯度下降是每次迭代使用一个样本来对参数进行更新。使得训练速度加快。

SGD with Momentum：SGD-M认为梯度下降过程可以加入惯性，在SGD基础上引入了一阶动量。
SGD with Nesterov Acceleration：是在SGD、SGD-M的基础上的进一步改进，改进点在于步骤1。
我们知道在时刻t的主要下降方向是由累积动量决定的，自己的梯度方向说了也不算，那与其看当前梯度
方向，不如先看看如果跟着累积动量走了一步，那个时候再怎么走。因此，NAG在步骤1，不计算当前位
置的梯度方向，而是计算如果按照累积动量走了一步，那个时候的下降方向。然后用下一个点的梯度方
向，与历史累积动量相结合，计算步骤2中当前时刻的累积动量。

Nesterov 的梯度项

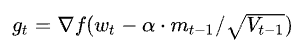
   MBGD小批量随机梯度下降：是对批量梯度下降以及随机梯度下降的一个折中办法。其思想是：每次迭代 使用 ** batch_size** 个样本来对参数进行更新。

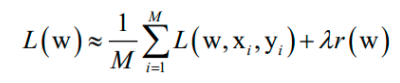
4.1.2 动量项Momentum

   为了加快梯度下降法的收敛速度，减少震荡，引入了动量项。动量项累积了之前迭代时的梯度值，加上此项之后的参数更新公式为：

   其中Vt+1是动量项，它取代了之前的梯度项。动量项的计算公式为

   它是上一时刻的动量项与本次梯度值的加权平均值，其中a 是学习率，u是动量项系数。如果按照时间t进行展开，则第t次迭代时使用了从1到t次迭代时的所有梯度值，且老的梯度值按 u 的系数 t 指数级衰减:

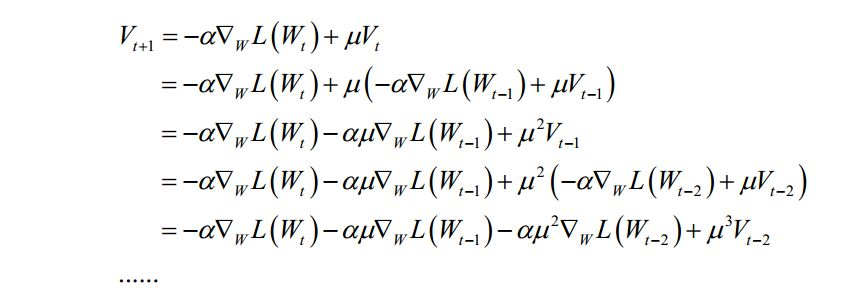
   动量项累积了之前迭代时的梯度值，使得本次迭代时沿着之前的惯性方向向前走。

4.1.3 AdaGrad算法

   AdaGrad算法是梯度下降法最直接的改进。
   梯度下降法依赖于人工设定的学习率，如果设置过小，收敛太慢，而如果设置太大，可能导致算法那不收敛，为这个学习率设置一个合适的值非常困难。对于经常更新的参数，我们已经积累了大量关于它的知识，不希望被单个样本影响太大，希望学习速率慢一些；对于偶尔更新的参数，我们了解的信息太少，希望能从每个偶然出现的样本身上多学一些，即学习速率大一些。
   AdaGrad算法利用二阶动量（迄今为止所有梯度值的平方和），即根据前几轮迭代时的历史梯度值动态调整学习率，且优化变量向量x的每一个分量 xi 都有自己的学习率。参数更新公式为：

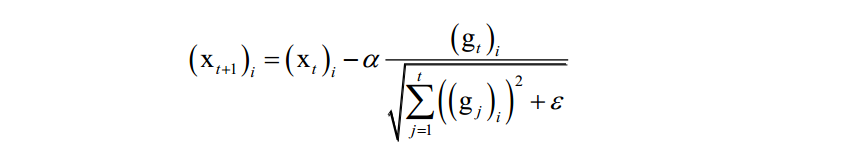
   其中a 是学习因子， gt是第t次迭代时参数的梯度向量， ε是平滑项，是一个很小的正数，为了避免除0操作，下标i表示向量的分量。和标准梯度下降法唯一不同的是多了分母中的这一项，它累积了到本次迭代为止梯度的历史值信息用于生成梯度下降的系数值。
   根据上式，历史导数值的绝对值越大（参数更新越频繁）分量学习率越小，反之越大。虽然实现了自适应学习率，但这种算法还是存在问题：需要人工设置一个全局的学习率 a，随着时间的累积，上式中的分母会越来越大，导致学习率趋向于0，参数无法有效更新，可能会使得训练过程提前结束，即便后续还有数据也无法学到必要的知识。

4.1.4 RMSProp

   RMSProp算法是对AdaGrad的改进，避免了长期累积梯度值所导致的学习率趋向于0的问题。具体做法是由梯度值构造一个向量RMS，初始化为0，按照衰减系数累积了历史的梯度平方值。更新公式为：

   AdaGrad直接累加所有历史梯度的平方和，而这里将历史梯度平方值按照 [公式] 衰减之后再累加。参数更新公式为：δt，衰减之后再累加。参数更新公式为：

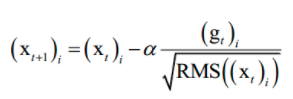
   其中 δ是人工设定的参数，与AdaGrad一样，这里也需要人工指定的全局学习率a。

4.1.5 AdaDelta算法

   AdaDelta算法也是对AdaGrad的改进，避免了长期累积梯度值所导致的学习率趋向于0的问题，另外，还去掉了对人工设置的全局学习率的依赖。而只关注过去一段时间窗口的下降梯度。这也就是AdaDelta名称中Delta的来历。
   假设要优化的参数为x，梯度下降法第t次迭代时计算出来的参数梯度值为 [公式] 。算法首先初始化如下两个向量为0向量：

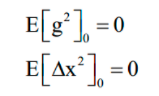
其中前者是梯度平方（对每个分量分别平分）的累计值，更新公式为：

在这里g2 是向量每个元素分别计算平方，后面所有的计算公式都是对向量的每个分量进行。接下来计算如下RMS量：

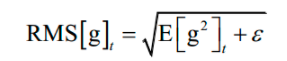
这也是一个向量，计算时分别对向量的每个分量进行。然后计算参数的更新值：

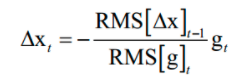
分子的计算公式和这个类似。这个更新值同样通过梯度来构造，只不过学习率是通过梯度的历史值确定的。更新公式为：

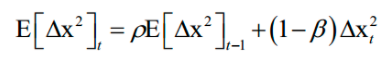
参数更新的迭代公式为：

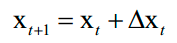
4.1.6 Adam算法

   Adam算法是前述方法的集大成者。它整合了自适应学习率与动量项。SGD-M在SGD基础上增加了一阶动量，AdaGrad和AdaDelta在SGD基础上增加了二阶动量。把一阶动量和二阶动量都用起来，就是Adam了——Adaptive + Momentum。
   算法用梯度构造了两个向量m和v，前者为动量项，后者累积了梯度的平方和（二阶动量），用于构造自适应学习率。它们的初始值为0，更新公式为：

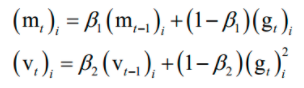
   其中β1 ， β2是人工指定的超参数，i为向量的分量下标。依靠这两个值构造参数的更新值，参数的更新公式为：在这里，m类似于动量项，用v来构造学习率。

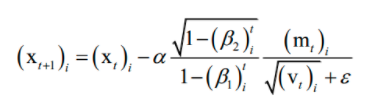
   在这里，m类似于动量项，用v来构造学习率。

4.1.7 Nadam

   最后是Nadam。Adam是集大成者，但遗漏了Nesterov，加上它。Nesterov + Adam = Nadam。

4.1.8 SAG,SVRG,SAGA

   最常用的优化算法SGD(随机梯度下降算法)，由于每次迭代方向都是随机选择的，所以产生了下降方向的噪音的方差。正是由于这个方差的存在，所以导致了SGD在每次迭代（使用固定步长）时，最终是收敛不到最优值的，最优间隔最终趋于一个和方差有关的定值。为了克服这一点，采取一种办法，想要让方差呈递减趋势下降，那么最终算法将会以线性速度收敛于最优值。根据这个想法，我们主要有SAG,SVRG,SAGA三种最常用的算法。
   SVRG(stochastic variance reduced gradient):SVRG相对于SGD来说在最优值附近几乎没有震荡，也没有噪音，SGD在最优值附近震荡明显。而且SVRG下降方向的方差最终趋于零，明显比SGD小。
   SAG（Stochastic Average Gradient）：它既有SGD算法计算量小的特点，又具有像FGD一样的线性收敛速度。
   SAGA算法：SAGA算法是SAG算法的一个加速版本，和SAG一样，它既不在一个循环里面操作，也不计算批量梯度(除了在初始点)，在每次迭代中，它都计算随机向量作为前期迭代中随机梯度的平均值。SAGA也减少了噪音的影响。(SAGA和SAG的区别就是一个是无偏估计，一个不是)

4.2 牛顿法

   牛顿法是二阶优化技术，利用了函数的一阶和二阶导数信息，直接寻找梯度为0的点。牛顿法的迭代公式为：

   其中H为Hessian矩阵，g为梯度向量。牛顿法不能保证每次迭代时函数值下降，也不能保证收敛到极小值点。在实现时，也需要设置学习率，原因和梯度下降法相同，是为了能够忽略泰勒展开中的高阶项。学习率的设置通常采用直线搜索（line search）技术。
在实现时，一般不直接求Hessian矩阵的逆矩阵，而是求解下面的线性方程组：

   其解d称为牛顿方向。迭代终止的判定依据是梯度值充分接近于0，或者达到最大指定迭代次数。
   缺点：牛顿法比梯度下降法有更快的收敛速度，但每次迭代时需要计算Hessian矩阵，并求解一个线性方程组，运算量大。另外，如果Hessian矩阵不可逆，则这种方法失效。对牛顿法更全面的介绍可以阅读SIGAI之前的公众号文章“理解牛顿法”。
   牛顿法在logistic回归，AdaBoost算法等机器学习算法中有实际应用。

4.2.1 拟牛顿法

   牛顿法在每次迭代时需要计算出Hessian矩阵，并且求解一个以该矩阵为系数矩阵的线性方程组，Hessian矩阵可能不可逆。为此提出了一些改进的方法，典型的代表是拟牛顿法。
   拟牛顿法的思路是不计算目标函数的Hessian矩阵然后求逆矩阵，而是通过其他手段得到一个近似Hessian矩阵逆的矩阵。具体做法是构造一个近似Hessian矩阵或其逆矩阵的正定对称矩阵，用该矩阵进行牛顿法的迭代。
   DFP，BFGS，L-BFGS，使用最多的是L-BFGS。
   L-BFGS：
   我们知道算法在计算机中运行的时候是需要很大的内存空间的.就像我们解决函数最优化问题常用的梯度下降,它背后的原理就是依据了泰勒一次展开式.泰勒展开式展开的次数越多,结果越精确,没有使用三阶四阶或者更高阶展开式的原因就是目前硬件内存不足以存储计算过程中演变出来更复杂体积更庞大的矩阵.L-BFGS算法翻译过来就是有限内存中进行BFGS算法,L是limited memory的意思.

4.2.1 可信域牛顿法

   标准牛顿法可能不会收敛到一个最优解，也不能保证函数值会按照迭代序列递减。解决这个问题可以通过调整牛顿方向的步长来实现，目前常用的方法有两种：直线搜索和可信区域法。可信域牛顿法是截断牛顿法的一个变种，用于求解带界限约束的最优化问题。在可信域牛顿法的每一步迭代中，有一个迭代序列xk ，一个可信域的大小 △k ，以及一个二次目标函数：

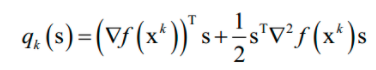
   这个式子可以通过泰勒展开得到，忽略二次以上的项，这是对函数下降值：

   的近似。算法寻找一个sk ，在满足约束条件丨丨s丨丨 ≤△k 下近似最小化 qk (s)。接下来检查如下比值以更新wk和△k ：

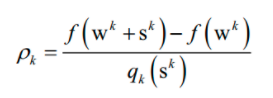
   是函数值的实际减少量和二次近似模型预测方向导致的函数减少量的比值。根据之前的计算结果，再动态调整可信域的大小。
   可信域牛顿法在logistic回归，线性支持向量的求解时有实际的应用，具体可以阅读liblinear开源库。

5 其他方法

5.1 分治法

   分治法是一种算法设计思想，它将一个大的问题分解成子问题进行求解。根据子问题解构造出整个问题的解。在最优化方法中，具体做法是每次迭代时只调整优化向量x的一部分分量，其他的分量固定住不动。

5.2 坐标下降法

   坐标下降法的基本思想是每次对一个变量进行优化，这是一种分治法。假设要求解的优化问题为;
   坐标下降法求解流程为每次选择一个分量 [公式] 进行优化，将其他分量固定住不动，这样将一个多元函数的极值问题转换为一元函数的极值问题。如果要求解的问题规模很大，这种做法能有效的加快速度。
   坐标下降法在logistic回归，线性支持向量的求解时有实际的应用，具体可以阅读liblinear开源库。

5.3 SMO算法

   SMO算法也是一种分治法，用于求解支持向量机的对偶问题。加上松弛变量和核函数后的对偶问题为：

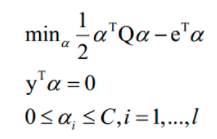
   SMO算法的核心思想是每次在优化变量中挑出两个分量 ai 和aj进行优化，让其他分量固定，这样能保证满足等式约束条件。之所以要选择两个变量进行优化而不是选择一个变量，是因为这里有等式约束，如果只调整一个变量的值，将会破坏等式约束。
假设选取的两个分量为ai和 aj ，其他分量都固定即当成常数。对这两个变量的目标函数是一个二元二次函数。这个问题还带有等式和不等式约束条件。对这个子问题可以直接求得公式解，就是某一区间内的一元二次函数的极值。

5.4 分阶段优化

   分阶段优化的做法是在每次迭代时，先固定住优化变量x一部分分量a不动，对另外一部分变量b进行优化；然后再固定住b不动，对b进行优化。如此反复，直至收敛到最优解处。
   AdaBoost算法是这种方法的典型代表。AdaBoost算法在训练时采用了指数损失函数：

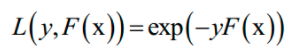
   由于强分类器是多个弱分类器的加权和，代入上面的损失函数中，得到算法训练时要优化的目标函数为：

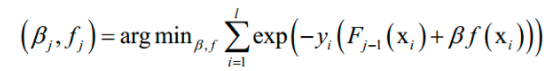
   这里将指数损伤函数拆成了两部分，已有的强分类器 Fj-1，以及当前弱分类器f对训练样本的损失函数，前者在之前的迭代中已经求出，因此可以看成常数。这样目标函数可以简化为：


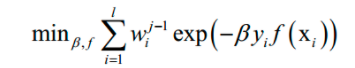
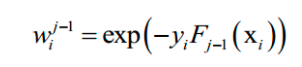
   这个问题可以分两步求解，首先将弱分类器权重β 看成常数，得到最优的弱分类器f。得到弱分类器之后，再优化它的权重系数β。

5.5 动态规划算法

   动态规划也是一种求解思想，它将一个问题分解成子问题求解，如果整个问题的某个解是最优的，则这个解的任意一部分也是子问题的最优解。这样通过求解子问题，得到最优解，逐步扩展，最后得到整个问题的最优解。
   隐马尔可夫模型的解码算法（维特比算法），强化学习中的动态规划算法是这类方法的典型代表，此类算法一般是离散变量的优化，而且是组合优化问题。前面讲述的基于导数的优化算法都无法使用。动态规划算法能高效的求解此类问题，其基础是贝尔曼最优化原理。一旦写成了递归形式的最优化方程，就可以构造算法进行求解。

6、如何选择优化方法

   选择优化器的问题在于，由于no-free-lunch定理，没有一个单一的优化器可以在所有场景中超越其他的。事实上，优化器的性能高度依赖于设置。所以，中心问题是：哪个优化器最适合我的项目的特点。
   在深度学习中，几乎所有流行的优化器都基于梯度下降。这意味着他们反复估计给定的损失函数L的斜率，并将参数向相反的方向移动(因此向下爬升到一个假设的全局最小值)。这种优化器最简单的例子可能是随机梯度下降(或SGD)，自20世纪50年代以来一直使用。在2010年代，自适应梯度的使用，如AdaGrad或Adam已经变得越来越流行了。然而，最近的趋势表明，部分研究界重新使用SGD而不是自适应梯度方法。此外，当前深度学习的挑战带来了新的SGD变体，如LARS或LAMB。
   如何选择正确的优化器？：
   在决定使用某个优化器之前应该问自己的三个问题。
   （1）与你的数据集和任务类似的state-of-the-art的结果是什么?使用过了哪些优化器，为什么？
   如果你正在使用新的机器学习方法，可能会有一篇或多篇涵盖类似问题或处理类似数据的可靠论文。通常，论文的作者已经做了广泛的交叉验证，并且只报告了最成功的配置。试着理解他们选择优化器的原因。
   （2）你的数据集是否具有某些优化器的优势？如果有，是哪些，如何利用这些优势？
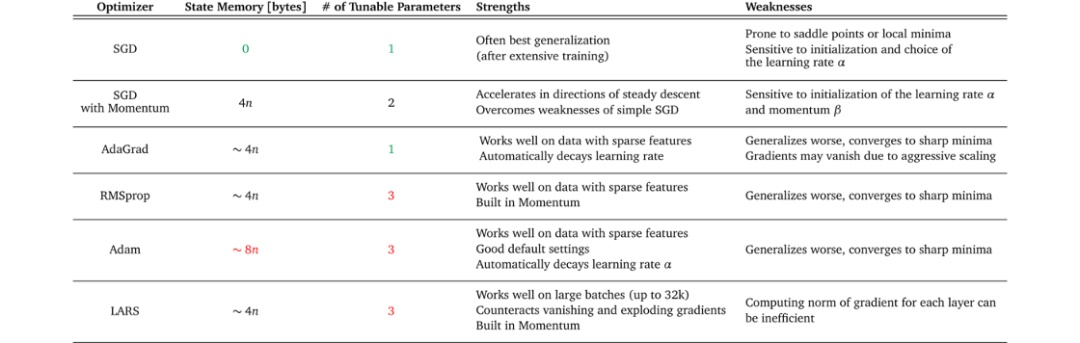
   某些优化器在具有稀疏特征的数据上表现得非常好，而另一些优化器在将模型应用于之前未见过的数据时可能表现得更好。一些优化器在大batch中工作得很好，而另一些优化器可以收敛到很陡峭的极小值但是泛化效果不好。

   （3）你的项目所具有资源是什么？
   项目中可用的资源也会影响选择哪个优化器。计算限制或内存约束，以及项目的时间表可以缩小可行选择的范围。再次查看表1，你可以看到不同的内存需求和每个优化器的可调参数数量。此信息可以帮助你评估你的设置是否支持优化器所需的资源。
   作为一个经验法则：如果你有资源找到一个好的学习率策略，带动量的SGD是一个可靠的选择。如果你需要快速的结果而不需要大量的超参数调优，请使用自适应梯度方法。

参考文献
一个框架看懂优化算法之异同 SGD/AdaGrad/Adam
https://zhuanlan.zhihu.com/p/32230623
机器学习中的最优化算法总结
https://zhuanlan.zhihu.com/p/42689565

最后

以上就是勤劳菠萝为你收集整理的优化算法详解的全部内容，希望文章能够帮你解决优化算法详解所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。