数学建模 现代优化算法

现代优化算法是20世纪80年代初兴起的启发式算法,包括禁忌搜索(Tabu Search),模拟退火(Simulated Annealing),遗传算法(Genetic Algorithms)和人工神经网络(Neural Network)等,主要用于解决各种实际应用问题.这些算法都有1个共同的目标:求NP-hard组合优化问题的全局最优解.但NP-hard理论限制它们只能以启发式的算法来求解问题.现代优化算法用于解决组合优化问题,如TSP问题(Traveling Salesman Problem),QAP问题(Quadratic Assignment Problem),JSP问题(Job-shop Scheduling Problem)等.

一.模拟退火算法
1.简介
(1)退火:

模拟退火算法的出现得益于材料统计力学的研究成果.统计力学表明材料中粒子的不同结构对应于粒子的不同能量水平:在高温条件下,粒子的能量较高,可以自由运动和重新排列;在低温条件下,粒子能量较低.如果从高温开始缓慢降温(该过程称为退火),粒子就可以在每个温度下达到热平衡.当系统被完全冷却时,就形成处于最小能量状态的晶体

如果用粒子的能量定义材料的状态,Metropolis算法用1个简单的数学模型描述了退火过程.假设材料在状态$i$下的能量为$E(i)$,那么材料在温度$T$时从状态$i$进入状态$j$就遵循如下规律:
①若$E(j)\le E(i)$,则接受该状态转换
②若$E(j)>E(i)$,则该状态转换以如下概率被接受:$$e^{\frac{E(i)-E(j)}{KT}}$$其中$K$为玻尔兹曼常数,$T$为材料温度.在某个特定温度下进行了充分的转换后,材料将达到热平衡,这时材料处于状态$i$的概率满足玻尔兹曼分布::$$P_T(X=i)=\frac{e^{-\frac{E(i)}{KT}}}{\sum _{j\in S}{e}^{-\frac{E(j)}{KT}}}$$其中$X$为材料当前状态的随机变量,$S$为所有状态构成的集合.显然$$\underset{T\to \infty }{\lim }{P}_T(X=i)=\frac{1}{|S|}$$其中$|S|$为集合$S$中状态的数量.这表明所有状态在高温下具有相同的概率;而当温度下降时,有$$\begin{gathered} \underset{T\to 0}{\lim }\frac{e^{-\frac{E(i)-E_{min}}{KT}}}{\sum _{j\in S}{e}^{-\frac{E(j)-E_{min}}{KT}}}=\underset{T\to 0}{\lim }\frac{e^{-\frac{E(i)-E_{min}}{KT}}}{\sum _{j\in S_{min}}{e}^{-\frac{E(j)-E_{min}}{KT}}+\sum _{j\notin S_{min}}{e}^{-\frac{E(j)-E_{min}}{KT}}} \\ =\underset{T\to 0}{\lim }\frac{e^{-\frac{E(i)-E_{min}}{KT}}}{\sum _{j\in S_{min}}{e}^{-\frac{E(j)-E_{min}}{KT}}}=\{\begin{array}{l}\frac{1}{|S_{min}|},i\in S_{min}\\ 0,其他\end{array} \end{gathered}$$其中 E m i n = min ⁡ j ∈ S E j , S m i n = { i   ∣   E ( i ) = E m i n } E_{min}=underset{j∈S}{min}{E_j},S_{min}={i,|,E(i)=E_{min}} Emin​=j∈Smin​Ej​,Smin​={i∣E(i)=Emin​}.这表明当温度降至很低时,材料会以很大概率进入最小能量状态

(2)模拟退火:

假定要解决1个寻找最小值的优化问题,将模拟退火的思想应用于优化问题就得到模拟退火寻优方法

考虑这样1个优化问题:优化函数为$f:x\to R^{+}(x\in S)$.其中$x$表示问题的1个可行解; R + = { y   ∣   y ∈ R , y ≥ 0 } . N ( x ) ⊆ S R^+={y,|,y∈R,y≥0}.N(x)sube S R+={y∣y∈R,y≥0}.N(x)⊆S表示$x$的1个邻域.首先给定1个初始温度$T_0$和1个初始解$x(0)$,并由$x(0)$生成下1个解$x^{\prime }\in N[X(0)]$,并按如下概率决定是否接受$x^{\prime }$作为1个新解$x(1)$:$$P(x(0)\to x^{\prime })=\{\begin{array}{l}1,f(x^{\prime })<f(x(0))\\ e^{-\frac{f(x^{\prime })-f(x(0))}{T_0}},其他\end{array}$$更一般地,对某个温度$T_i$和解$x(k)$,可以生成1个解$x^{\prime }$,按如下概率决定是否接受$x^{\prime }$作为1个新解$x(k+1)$:$$P(x(k)\to x^{\prime })=\{\begin{array}{l}1,f(x^{\prime })<f(x(k))\\ e^{-\frac{f(x^{\prime })-f(x(k))}{T_i}},其他\end{array}(12.1)$$在温度$T_i$下,经过多次转移后降低到温度$T_{i+1}<T_i$,然后重复上述过程.因此整个优化过程就是寻找新解和缓慢降温交替进行的过程,最终的解是对该问题寻优的结果.注意到在每个$T_i$下,所得的的新状态$x(k+1)$完全依赖于前1个状态$x(k)$,而与之前的状态$x(0),x(1)...x(k-1)$无关,因此这是1个马尔可夫过程.使用马尔可夫过程对上述模拟退火的步骤进行分析,结果表明如果从任意$x(k)$生成$x^{\prime }$的概率在$N[x(k)]$中是均匀分布的,且新状态$x^{\prime }$被接受的概率满足式$(12.1)$,那么经过有限次转换,在$T_i$下的平衡态$x_i$的分布由下式给出:$$P_i(T_i)=\frac{e^{-\frac{f(x_i)}{T_i}}}{\sum _{j\in S}{e}^{-\frac{f(x_j)}{T_i}}}(12.2)$$当温度$T$降为0时,$x_i$的分布为$$P_i^{\ast }=\{\begin{array}{l}\frac{1}{|S_{min}|},x_i\in S_{min}\\ 0,其他\end{array}$$并且$$\sum _{x_i\in S_{min}}{P}_i^{\ast }=1$$这说明如果温度下降十分缓慢,因而在每个温度都有足够多次的状态转移,使之在每个温度下都达到热平衡,则全局最优解将以概率1被找到.也就是说,模拟退火算法可以找到全局最优解

(3)注意事项:

①理论上降温过程需要足够缓慢,以使得在每个温度下都达到热平衡.在计算机实现中,如果降温速度过慢,所得到的解的性能会比较令人满意,但算法会过慢,从而相对于简单的搜索算法不具有明显优势;但如果降温过快,则可能最终得不到全局最优解.因此使用时需要综合考虑解的性能和算法速度
②需要确定在每个温度下状态转换的结束准则.实际操作中可以考虑当连续$m_1$次转换都没有使状态发生变化时就结束该温度下的状态转换;最终温度可以确定为1个提前决定好的较小的值$T$,或在连续$m_2$个温度下的状态转换都没有使状态发生变化时就结束算法
③初始温度的选择和确定邻域的方法也需要恰当

2.实例
(1)问题:

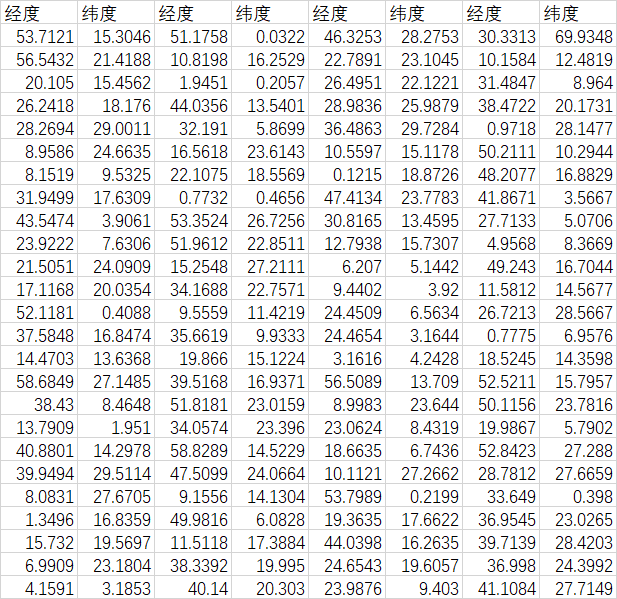
已知100个目标的经纬度如下表:

我方基地的经纬度为$(70,40)$,飞机的速度为$1000km/h$且续航时间充分长.要派1架飞机从基地出发,侦察完所有目标再返回.在每个目标处的侦察时间不计,求飞机花费的时间

(2)求解步骤:

这是1个旅行商问题:将基地编号为1,目标编号依次为2,3…101,最后再将基地编号为102以便于计算.距离矩阵$D=(d_{ij}{)}_{102\times 102}$,其中$d_{ij}$表示$i,j(i,j=1,2...102)$两点间的距离.可知$D$为实对称矩阵.则问题就是求从点1出发,走遍所有中间点,最后到达点102的最短路径.

问题中给出的是地理坐标,需要再求出2点间的距离.设$A,B$的地理坐标分别为$(x_1,y_1),(x_2,y_2)$,过$A,B$的大圆的劣弧长即为2点间的距离.以地心作为原点$O$,以赤道平面为$XOY$平面,以$0°$经线圈所在的平面为为$XOZ$平面建立3维直角坐标系,则$A,B$的直角坐标分别为$$\begin{gathered} A:(R\cos (x_1)\cos (y_1),R\sin (x_1)\cos (y_1),R\sin (y_1)) \\ B:(R\cos (x_2)\cos (y_2),R\sin (x_2)\cos (y_2),R\sin (y_2)) \end{gathered}$$其中$R=6370$为地球半径.则$A,B$间的距离为$$d=R\arccos (\frac{OA\cdot OB}{|OA|\cdot |OB|})$$化简,得$$d=R\arccos [\cos (x_1-x_2)\cos (y_1)\cos (y_2)+\sin (y_1)\sin (y_2)]$$

用于求解的模拟退火算法描述如下:
①解空间:解空间$S$可表示为 { 1 , 2...102 } {1,2...102} {1,2...102}的所有固定起点和终点的循环排列集合,即 S = { ( π 1 , π 2 . . . π 102 )   ∣   π 1 = 1 , ( π 2 , π 3 . . π 101 ) 为 { 2 , 3...101 } 的 循 环 排 列 , π 102 = 102 } S={(pi_1,pi_2...pi_{102}),|,pi_1=1,(pi_2,pi_3..pi_{101})为{2,3...101}的循环排列,pi_{102}=102} S={(π1​,π2​...π102​)∣π1​=1,(π2​,π3​..π101​)为{2,3...101}的循环排列,π102​=102}其中每个循环排列表示侦察的1种回路,${\pi }_i=j$表示第$i-1$个侦察$j$.可选择初始解为$(1,2...102)$,或用蒙特卡洛法求得1个较好的初始解
②目标函数:目标函数(也称代价函数)为要侦察所有目标所要走的路径长度.要求$$minf({\pi }_1,{\pi }_2...{\pi }_{102})=\sum _{i=1}^{101}{d}_{{\pi }_i{\pi }_{i+1}}$$
③新解的产生:设上1次迭代得到的解为${\pi }_1...{\pi }_{u-1}{\pi }_u{\pi }_{u+1}...{\pi }_{v-1}{\pi }_v{\pi }_{v+1}...{\pi }_{w-1}{\pi }_w{\pi }_{w+1}...{\pi }_{102}$
$Ⅰ.2$变换法:任选序号$u,v$,交换$u,v$的顺序,则新路径为${\pi }_1...{\pi }_{u-1}{\pi }_v{\pi }_{u+1}...{\pi }_{v-1}{\pi }_u{\pi }_{v+1}...{\pi }_{w-1}{\pi }_w{\pi }_{w+1}...{\pi }_{102}$
$Ⅱ.3$变换法:任选序号$u,v,w$,将$u,v$间的路径插到$w$之后,则新路径为${\pi }_1...{\pi }_{u-1}{\pi }_{v+1}...{\pi }_{w-1}{\pi }_w{\pi }_u...{\pi }_v{\pi }_{w+1}...{\pi }_{102}$
④代价函数差:对2变换法,路径差可表示为$$\Delta f=(d_{{\pi }_{u-1}{\pi }_v}+d_{{\pi }_u{\pi }_{v+1}})-(d_{{\pi }_{u-1}{\pi }_u}+d_{{\pi }_v{\pi }_{v+1}})$$
⑤接受准则:接受准则为$$P=\{\begin{array}{l}1,\Delta f<0\\ e^{-\frac{\Delta f}{T}},\Delta f\ge 0\end{array}$$
⑥降温:利用选定的降温系数$\alpha$进行降温,取新的温度$T^{\prime }=\alpha T(T$为上1次迭代的温度$)$
⑦结束条件:用选定的终止温度$e=10^{-30}$进行判断,若$T<e$,则结束退火过程

(3)计算代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
sj0=load("E:DownloadsData1.txt");%加载数据
>> x=sj0(:,[1:2:8]);
>> x=x(:);
>> y=sj0(:,[2:2:8]);
>> y=y(:);
>> sj=[x y];
>> d1=[70,40];
>> sj=[d1;sj;d1];
>> sj=sj*pi/180;%将角度转换为弧度
>> d=zeros(102);%初始化距离矩阵d
>> for i=1:101
       for j=i+1:102
           d(i,j)=6370*acos(cos(sj(i,1)-sj(j,1))*cos(sj(i,2))*cos(sj(j,2))+sin(sj(i,2))*sin(sj(j,2)));
       end
   end
>> d=d+d';
>> path=[];%初始化巡航路径
>> long=inf;
>> rand('state',sum(clock));
>> for j=1:1000%求1个较好的初始解
         path0=[1,1+randperm(100),102];
         temp=0;
         for i=1:101
             temp=temp+d(path0(i),path0(i+1));
         end
         if temp<long
             path=path0;
             long=temp;
         end
     end
>> e=0.1^30;
>> L=20000;
>> at=0.999;
>> T=1;
>> for k=1:L%退火过程
         c=2+floor(100*rand(1,2));%产生新解
         c=sort(c);
         c1=c(1);
         c2=c(2);
         df=d(path(c1-1),path(c2))+d(path(c1),path(c2+1))-d(path(c1-1),path(c1))-d(path(c2),path(c2+1));%计算代价函数的增量
         if df<0
             path=[path(1:c1-1),path(c2:-1:c1),path(c2+1:102)];
             long=long+df;
         elseif exp(-df/T)>=rand
             path=[path(1:c1-1),path(c2:-1:c1),path(c2+1:102)];
             long=long+df;
         end
         T=T*at;
         if T<e
             break
         end
     end
>> path,long

path =

  1 至 25 列

     1    35    95    52   101    99    21    56   100    98    51    80    50     9    38    44    96     6    89    55    54    75     5     4    41

  26 至 50 列

    91    76    11    69    70    16    61    88    78    39    47    57    28    49    24    13    73    33    53    12    32    68     7    22    71

  51 至 75 列

    37    77    81    25    58    23    90    66    34    29    26    62    86     8    63    19    94    64    65    85    79    60    40    18    31

  76 至 100 列

    97    84    10    27    14    72    48    82    67    45     2    92    87    83    30    20    15    42    74    59    46    93    43    36     3

  101 至 102 列

    17   102


long =

   5.3338e+04

>> xx=sj(path,1);
>> yy=sj(path,2);
>> plot(xx,yy,'-*')%画出巡航路径(见下图)

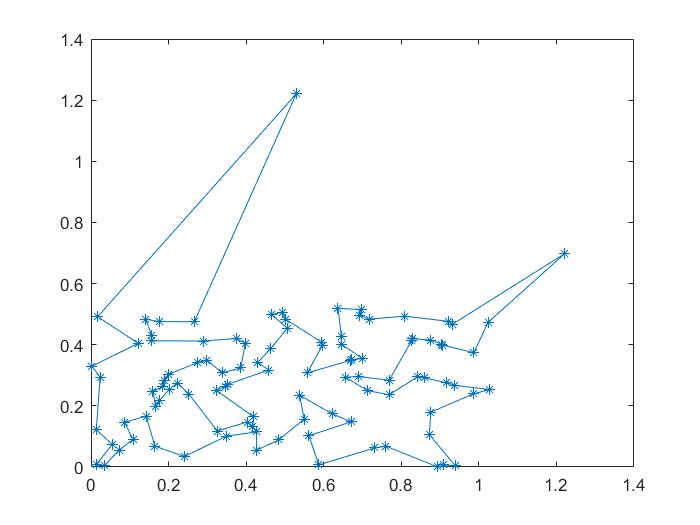
二.遗传算法
1.简介
(1)基本思想:

遗传算法(Genetic Algorithms;GA)是1种基于自然选择原理和自然遗传机制的搜索(寻优)算法,是通过模拟自然界中的生命进化机制来在人工系统中实现特定目标的优化.其实质是通过群体搜索技术,根据适者生存的原则逐代进化,最终得到最优解或准最优解

该算法需要进行以下操作:①初始群体的产生 ②求每个个体的适应度 ③根据适者生存的原则选择优良个体 ④将被选出的优良个体两两配对 ⑤通过随机交叉染色体上的基因并随机变异某些基因生成下1代群体 ⑥按此方法逐代进化,直到满足进化终止条件.具体的实现方法如下:
①根据具体问题确定可行解域;确定1种编码方法,以便用数值串或字符串表示可行解域中的每个解
②对每个解都应有1个度量好坏的依据,用1个函数表示(称为适应度函数),一般由目标函数构成
③确定群体规模$M$,交叉概率$p_c$,变异概率$p_m$,进化终止条件等
为了便于计算,一般令每代群体规模都相等;群体规模越大,越容易找到最优解,但需要的时间也越多;一般设置进化终止条件为进化到某1代就结束,或近似最优解达到某个精度就结束

(2)相关概念:

2.实例:

三.改进的遗传算法

最后

以上就是勤奋小懒猪最近收集整理的关于数学建模 现代优化算法的全部内容，更多相关数学建模内容请搜索靠谱客的其他文章。