同步于Buracag的博客

优化问题一般都是通过迭代的方式来求解：通过猜测一个初始的估计$x_0$，然后不断迭代产生新的估计$x_1,x_2,...x_t$，希望$x_t$最终收敛到期望的最优解$x^{\ast }$。

一个好的优化算法应该是在一定的时间或空间复杂度下能够快速准确地找到最优解。同时，好的优化算法受初始猜测点的影响较小，通过迭代能稳定地找到最优解$x^{\ast }$的邻域，然后迅速收敛于$x^{\ast }$。

优化算法中常用的迭代方法有线性搜索和置信域方法等。线性搜索的策略是寻找方向和步长，具体算法有梯度下降法、牛顿法、共轭梯度法等。在文章中也简要介绍过梯度下降的概念，这里为使得整个体系完整故重新记录一下。

1. 全局最优和局部最优

对于很多非线性优化问题，会存在若干个局部的极小值。局部最小值，或局部最优解$x^{\ast }$定义为：存在一个$\delta >0$，对于所有的满足$\Vert x-x^{\ast }\Vert \le \delta$的x，公式$f(x^{\ast })\le f(x)$成立。也就是说，在$x^{\ast }$的附近区域内，所有的函数值都大于或者等于$f(x^{\ast })$。

对于所有的$x\in A$，都有$f(x^{\ast })\le f(x)$成立，则$x^{\ast }$为全局最小值，或全局最优解。一般的，求局部最优解是容易的，但很难保证其为全局最优解。对于线性规划或凸优化问题，局部最优解就是全局最优解。

要确认一个点$x^{\ast }$是否为局部最优解，通过比较它的邻域内有没有更小的函数值是不现实的。如果函数$f(x)$是二次连续可微的，我们可以通过检查目标函数在点$x^{\ast }$的梯度$\nabla f(x^{\ast })$和Hessian矩阵${\nabla }^{2}f(x^{\ast })$来判断。

定理1 局部最小值的一阶必要条件： 如果$x^{\ast }$为局部最优解并且函数$f$在$x^{\ast }$的邻域内一阶可微，则在$\nabla f(x^{\ast })=0$。

证明. 如果函数$f(x)$是连续可微的，根据泰勒展开公式（Taylor’s Formula），函数$f(x)$的一阶展开可以近似为
$$f(x^{\ast }+\Delta x)=f(x^{\ast })+\Delta x^T\nabla f(x^{\ast })\text{\hspace{1em}(1)}$$
假设$\nabla f(x^{\ast })̸=0$，则可以找到一个$\Delta x$（比如$\Delta x=-\alpha \nabla f(x^{\ast })$，$\alpha$为很小的正数），使得
$$f(x^{\ast }+\Delta x)-f(x^{\ast })=\Delta x^T\nabla f(x^{\ast })\le 0\text{\hspace{1em}(2)}$$

这和局部最优的定义矛盾。

定理2 局部最优解的二阶必要条件： 如果$x^{\ast }$为局部最优解并且函数$f$在$x^{\ast }$的领域内二阶可微，则$\nabla f(x^{\ast })=0,{\nabla }^{2}f(x^{\ast })$为半正定矩阵。

证明. 如果函数$f(x)$是二次连续可微的，函数$f(x)$的二阶展开可以近似为
$$f(x^{\ast }+\Delta x)=f(x^{\ast })+\Delta x^T\nabla f(x^{\ast })+\frac{1}{2}\Delta x^T({\nabla }^{2}f(x^{\ast }))\Delta x\text{\hspace{1em}(3)}$$
由一阶必要性定理可知$\nabla f(x^{\ast })=0$，则
$$f(x^{\ast }+\Delta x)-f(x^{\ast })=\frac{1}{2}\Delta x^T({\nabla }^{2}f(x^{\ast }))\Delta x\ge 0\text{\hspace{1em}(4)}$$
即Hessian矩阵${\nabla }^{2}f(x^{\ast })$为半正定矩阵。

2. 梯度下降法

梯度下降法（Gradient Descent Method），也叫最速下降法（Steepest Descend Method），经常用来求解无约束优化的极小值问题。

对于函数$f(x)$，如果$f(x)$在点$x_t$附近是连续可微的，那么$f(x)$下降最快的方向是$f(x)$在$x_t$点的梯度方法的反方向。根据泰勒一阶展开公式，
$$f(x_{t+1})=f(x_t+\Delta x)\approx f(x_t)+\Delta x^T\nabla f(x_t)\text{\hspace{1em}(5)}$$
要使得$f(x_{t+1})<f(x_t)$，就得使$\Delta x^T\nabla f(x_t)<0$。我们取$\Delta x=-\alpha \nabla f(x_t)$。如果$\alpha >0$为一个够小数值时，那么$f(x_{t+1})<f(x_t)$ 成立。

这样我们就可以从一个初始值$x_0$出发，通过迭代公式
$$x_{t+1}=x_t-{\alpha }_t\nabla f(x_t),t\ge 0\text{\hspace{1em}(6)}$$
生成序列$x_0,x_1,x_2,...$ 使得
$$f(x_0)\ge f(x_1)\ge f(x_2)\ge ...\text{\hspace{1em}(7)}$$
如果顺利的话，序列($x_n$) 收敛到局部最优解$x^{\ast }$。注意每次迭代步长$\alpha$可以改变，但其取值必须合适，如果过大就不会收敛，如果过小则收敛速度太慢。

梯度下降法的示例过程可以参见下图：

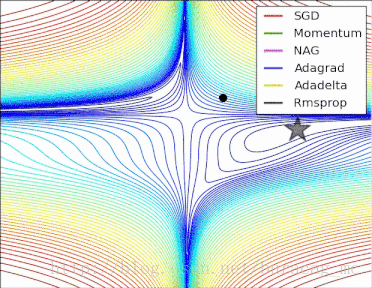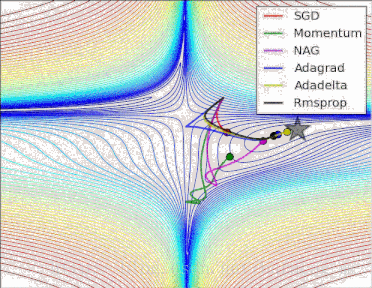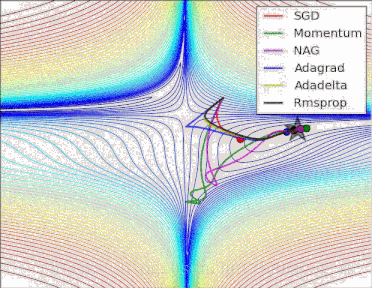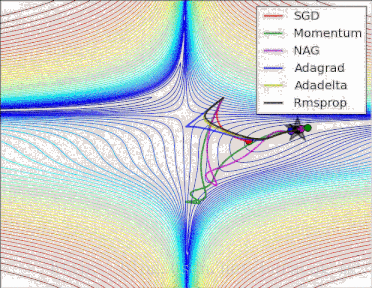
梯度下降法为一阶收敛算法，当靠近极小值时梯度变小，收敛速度会变慢，并且可能以“之字形”的方式下降。如果目标函数为二阶连续可微，我们可以采用牛顿法。牛顿法为二阶收敛算法，收敛速度更快，但是每次迭代需要计算Hessian矩阵的逆矩阵，复杂度较高。相反，如果我们要求解一个最大值问题，就需要向梯度正方向迭代进行搜索，逐渐接近函数的局部极大值点，这个过程则被称为梯度上升法（GradientAscent）。

后面准备专门整理一份梯度下降中关于批量梯度下降(BGD)、随机梯度下降(SGD)、小批量梯度下降(MBGD)、Momentum、Adagrad等资料。

主要参考https://github.com/nndl/nndl.github.io

最后

以上就是迅速可乐最近收集整理的关于数学优化2-优化算法1. 全局最优和局部最优2. 梯度下降法的全部内容，更多相关数学优化2-优化算法1.内容请搜索靠谱客的其他文章。