概述
解决常微分数值解的情况分为刚性问题与非刚性问题。问题不同使用的函数不同，使用错了，迭代时间久了，反而效果不是很明显。
非刚性问题
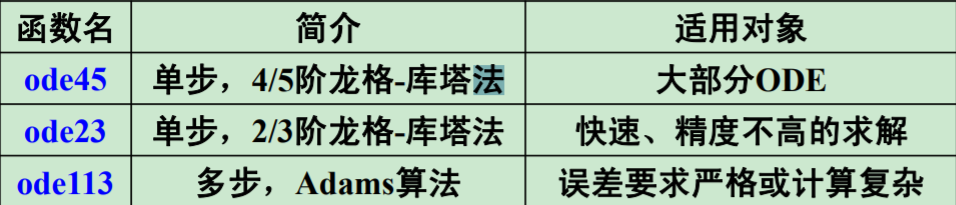
刚性问题定义及求解器使用
所谓刚性问题，其数值解变化分量特别诡异，有时很慢，有时很快；变化快的分量很快趋于稳定值，而变化慢的分量缓慢趋于稳定值，变化快时，我们想要积分小步长，慢的趋于稳定的，我们想要步长放大。但是事与愿违，因此称这种在步长选择上有纠结的为刚性问题。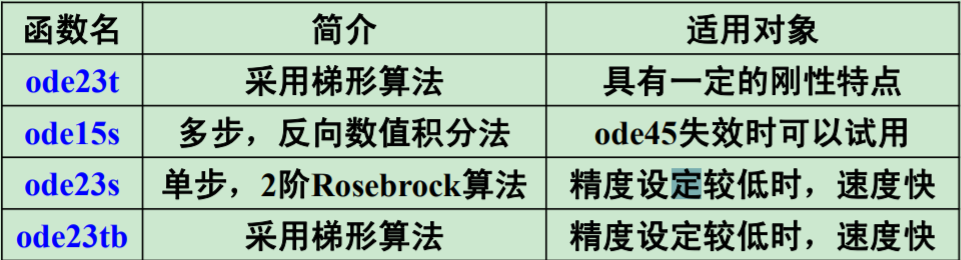
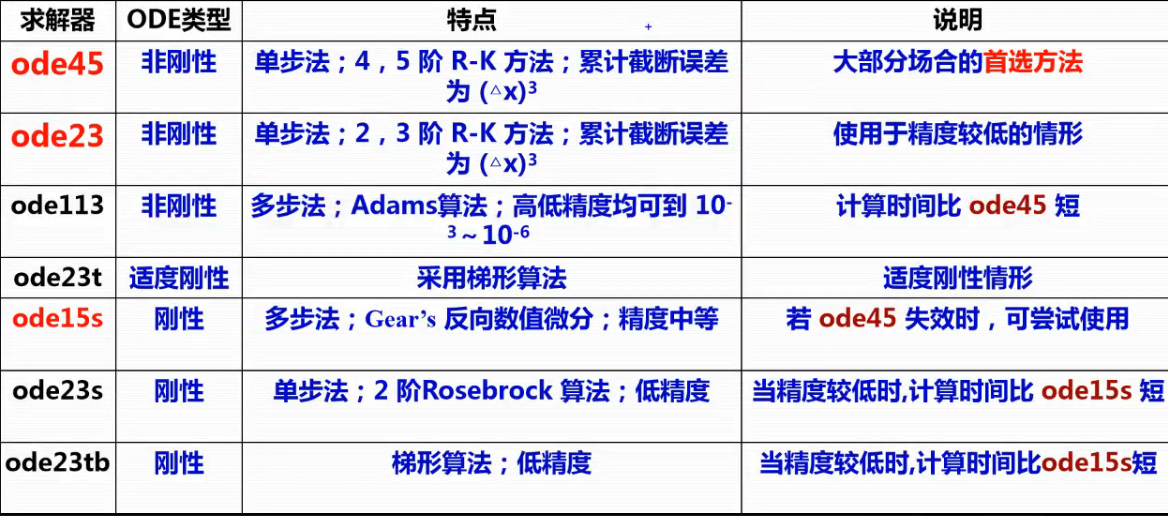
汇总版本ode使用指南
| 求解器 | 方法描述 | 使用场合 |
|---|---|---|
| ode23 | 2到3阶Runge-Kutta算法，低精度 | 非刚性 |
| ode45 | 4-5阶Runge-Kutta算法，中精度 | 非刚性 |
| ode113 | Adams算法，精度可到10的-3次到10^-4次 | 非刚性，计算时间比ode45快 |
| ode23t | 梯形算法 | 适度刚性 |
| ode15s | 反向数值微分算法，中精度 | 刚性 |
| ode23s | 2阶Rosebrock算法，低精度 | 刚性，当精度较低时，计算时间比ode15s短 |
| ode23tb | 梯形算法，低精度 | 刚性，当精度较低时，计算时间比ode15s短 |
| ode15i | 可变秩求法 | 完全隐形微分方程 |
最后
以上就是机智香烟为你收集整理的matlab刚性与非刚性情境下使用的ode求解器使用指南的全部内容，希望文章能够帮你解决matlab刚性与非刚性情境下使用的ode求解器使用指南所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
![[MATLAB]常微分方程数值求解(ode45 ode15s ode23 solver)](/uploads/reation/bcimg9.png)
发表评论 取消回复