本文讲述了两个使用 ode15s 解算刚性常微分方程的示例。MATLAB 拥有四个专用于刚性 ODE 的求解器。
- ode15s
- ode23s
- ode23t
- ode23tb
对于大多数刚性问题,ode15s 的性能最佳。但如果问题允许较宽松的误差容限,则 ode23s、ode23t 和 ode23tb 可能更加高效。
什么是刚性 ODE?
对于一些 ODE 问题,求解器采用的步长被强制缩小为与积分区间相比过小的级别,甚至在解曲线平滑的区域亦如此。这些步长可能过小,以至于遍历很短的时间区间都可能需要数百万次计算。这可能导致求解器积分失败,即使积分成功也需要花费很长时间。
导致 ODE 求解器出现此行为的方程称为刚性方程。刚性 ODE 造成的问题是,显式求解器(例如 ode45)获取解的速度慢得令人无法忍受。这是将 ode45 与 ode23 和 ode113 一同归类为非刚性求解器的原因所在。
专用于刚性 ODE 的求解器称为刚性求解器,它们通常在每一步中完成更多的计算工作。这样做的好处是,它们能够采用大得多的步长,并且与非刚性求解器相比提高了数值稳定性。
求解器选项
对于刚性问题,使用 odeset 指定 Jacobian 矩阵尤为重要。刚性求解器使用 Jacobian 矩阵 ∂ f i / ∂ y j partial f_i / partial y_j ∂fi/∂yj 来预测 ODE 在积分过程中的局部行为,因此提供 Jacobian 矩阵(或者对于大型稀疏方程组提供其稀疏模式)对于提高效率和可靠性而言至关重要。使用 odeset 的 Jacobian、JPattern 或 Vectorized 选项来指定 Jacobian 的相关信息。如果没有提供 Jacobian,则求解器将使用有限差分对其进行数值预测。
有关其他求解器选项的完整列表,请参阅 odeset。
示例:刚性 van der Pol 方程
van der Pol 方程为二阶 ODE
y 1 ′ ′ − μ ( 1 − y 1 2 ) y 1 ′ + y 1 = 0 , y''_1 - mu left( 1 - y_1^2right) y'_1+y_1=0, y1′′−μ(1−y12)y1′+y1=0,
其中 KaTeX parse error: Expected 'EOF', got '&' at position 5: mu &̲#62; 0 为标量参数。当 μ = 1 mu = 1 μ=1 时,生成的 ODE 方程组为非刚性方程组,可以使用 ode45 轻松求解。但如果将 μ mu μ 增大至 1000,则解会发生显著变化,并会在明显更长的时间段中显示振荡。求初始值问题的近似解变得更加复杂。由于此特定问题是刚性问题,因此专用于非刚性问题的求解器(如 ode45)的效率非常低下且不切实际。针对此问题应改用 ode15s 等刚性求解器。
通过执行代换 y 1 ′ = y 2 y'_1 = y_2 y1′=y2,将该 van der Pol 方程重写为一阶 ODE 方程组。生成的一阶 ODE 方程组为
y 1 ′ = y 2 y 2 ′ = μ ( 1 − y 1 2 ) y 2 − y 1 . begin{array}{cl} &y'_1 = y_2\ &y'_2 = mu (1-y_1^2) y_2 - y_1 . end{array} y1′=y2y2′=μ(1−y12)y2−y1.
vdp1000 函数使用 μ = 1000 mu = 1000 μ=1000 计算 van der Pol 方程。
function dydt = vdp1000(t,y)
dydt = [y(2); 1000*(1-y(1)^2)*y(2)-y(1)];
使用 ode15s 函数和初始条件向量 [2; 0],在时间区间 [0 3000] 上解算此问题。由于是标量,因此仅绘制解的第一个分量。
[t,y] = ode15s(@vdp1000,[0 3000],[2; 0]);
plot(t,y(:,1),'-o');
title('Solution of van der Pol Equation, mu = 1000');
xlabel('Time t');
ylabel('Solution y_1');
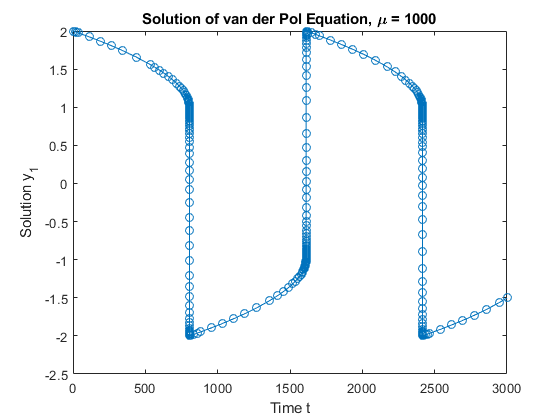
vdpode 函数也可以求解同一问题,但它接受的是用户指定的 μ mu μ 值。随着 μ mu μ 的增大,该方程组的刚性逐渐增强。
示例:稀疏 Brusselator 方程组
经典 Brusselator 方程组可能为大型刚性稀疏矩阵。Brusselator 方程组可模拟化学反应中的扩算,并表示为涉及 u u u、 v v v、 u ′ u' u′ 和 v ′ v' v′ 的方程组。
u i ′ = 1 + u i 2 v i − 4 u i + α ( N + 1 ) 2 ( u i − 1 − 2 i + u i + 1 ) v i ′ = 3 u i − u i 2 v i + α ( N + 1 ) 2 ( v i − 1 − 2 v i + v i + 1 ) begin{array}{cl} &u'_i=1+u_i^{2}v_i-4u_i+alpha( N + 1)^{2} (u_{i-1}-2_i+u_{i+1} ) \ &v'_i = 3u_i-u_i^{2}v_i + alpha( N+1) ^{2}( v_{i-1} - 2v_i+v_{i+1} ) end{array} ui′=1+ui2vi−4ui+α(N+1)2(ui−1−2i+ui+1)vi′=3ui−ui2vi+α(N+1)2(vi−1−2vi+vi+1)
函数文件 brussode 使用 α = 1 / 50 alpha = 1/50 α=1/50 在时间区间 [0,10] 上对这组方程进行求解。初始条件为
u j ( 0 ) = 1 + sin ( 2 π x j ) v j ( 0 ) = 3 , begin{array}{cl} &u_j(0) = 1+sin(2 pi x_j)\ &v_j(0) =3, end{array} uj(0)=1+sin(2πxj)vj(0)=3,
其中,当 i = 1 , . . . , N i=1,...,N i=1,...,N 时, x j = i / N + 1 x_j = i/N+1 xj=i/N+1。因此,该方程组中有 2 N 2N 2N 个方程,但如果这些方程按 u 1 , v 1 , u 2 , v 2 , . . . u_1,v_1,u_2,v_2,... u1,v1,u2,v2,... 的形式排序,则 Jacobian ∂ f / ∂ y partial f / partial y ∂f/∂y 为具有常量宽度 5 的带状矩阵。随着 N N N 的增大,此问题的刚性逐渐增强,并且 Jacobian 矩阵的稀疏性也逐渐增大。
函数调用 brussode(N)(其中 N > 2)为方程组中的 N(对应于网格点数量)指定值。默认情况下,brussode 使用 N = 20。
brussode 包含一些子函数:
嵌套函数 f(t,y) 用于编写 Brusselator 问题的方程组代码,并返回一个向量。
局部函数 jpattern(N) 返回由 1 和 0 组成的稀疏矩阵,从而显示 Jacobian 矩阵中非零值的位置。此矩阵将赋给 options 结构体的 JPattern 字段。ODE 求解器使用此稀疏模式,生成稀疏矩阵形式的 Jacobian 数值矩阵。在问题中提供此稀疏模式可将生成 2N×2N Jacobian 矩阵所需的函数计算量从 2N 次大幅减少至仅仅 4 次。
function brussode(N)
if nargin<1
N = 20;
end
tspan = [0; 10];
y0 = [1+sin((2*pi/(N+1))*(1:N)); repmat(3,1,N)];
options = odeset('Vectorized','on','JPattern',jpattern(N));
[t,y] = ode15s(@f,tspan,y0,options);
u = y(:,1:2:end);
x = (1:N)/(N+1);
figure;
surf(x,t,u);
view(-40,30);
xlabel('space');
ylabel('time');
zlabel('solution u');
title(['The Brusselator for N = ' num2str(N)]);
function dydt = f(t,y)
c = 0.02 * (N+1)^2;
dydt = zeros(2*N,size(y,2));
% preallocate dy/dt
i = 1;
dydt(i,:) = 1 + y(i+1,:).*y(i,:).^2 - 4*y(i,:) + c*(1-2*y(i,:)+y(i+2,:));
dydt(i+1,:) = 3*y(i,:) - y(i+1,:).*y(i,:).^2 + c*(3-2*y(i+1,:)+y(i+3,:));
i = 3:2:2*N-3;
dydt(i,:) = 1 + y(i+1,:).*y(i,:).^2 - 4*y(i,:) + ...
c*(y(i-2,:)-2*y(i,:)+y(i+2,:));
dydt(i+1,:) = 3*y(i,:) - y(i+1,:).*y(i,:).^2 + ...
c*(y(i-1,:)-2*y(i+1,:)+y(i+3,:));
i = 2*N-1;
dydt(i,:) = 1 + y(i+1,:).*y(i,:).^2 - 4*y(i,:) + c*(y(i-2,:)-2*y(i,:)+1);
dydt(i+1,:) = 3*y(i,:) - y(i+1,:).*y(i,:).^2 + c*(y(i-1,:)-2*y(i+1,:)+3);
end
% -------------------------------------------------------------------------
end
% ---------------------------------------------------------------------------
function S = jpattern(N)
B = ones(2*N,5);
B(2:2:2*N,2) = zeros(N,1);
B(1:2:2*N-1,4) = zeros(N,1);
S = spdiags(B,-2:2,2*N,2*N);
end
% ---------------------------------------------------------------------------
通过运行函数 brussode,对 N = 20 N=20 N=20 时的 Brusselator 方程组求解。
brussode
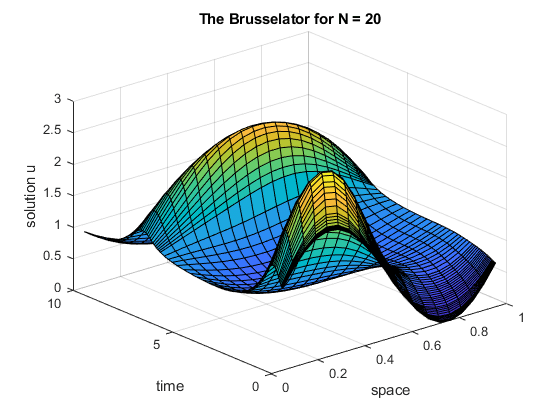
通过为 brussode 指定输入,对 N = 50 N=50 N=50 时的方程组求解。
brussode(50)
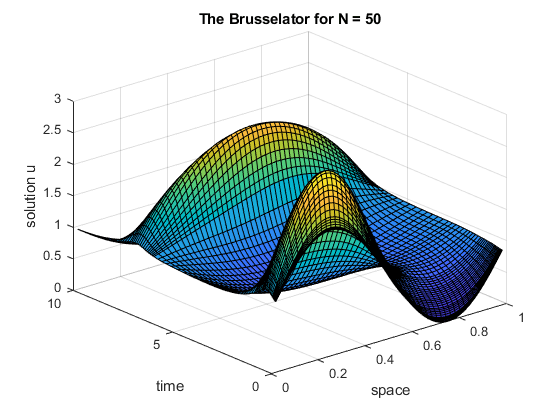
最后
以上就是烂漫手链最近收集整理的关于MATLAB 数学应用 微分方程 常微分方程 解算刚性ODE的全部内容,更多相关MATLAB内容请搜索靠谱客的其他文章。








发表评论 取消回复