Logistic曲线的参数估计
作者qq:2377389590欢迎探讨。
闲着无聊整理了一下课程设计的作业,老师给了我们数学模型,让我们根据数学模型原理写代码,因为小编从刚上大一就开始自学Matlab,《电力符合预测》这门课的老师以为我们三个班都会,其实三个班就是我一个人看懂并写出来了,最后三个班上交了一样的代码,幸好老师没有应为一样而我们挂科。聪明的小编,在此夸夸自己。废话少说,原理如下:
1844或1845年,比利时数学家Pierre François Verhulst提出了logistic方程,这是一个对S型曲线进行数学描述的模型。一百多年来,这个方程多次应用于一些特殊的领域建模与预测,例如单位面积内某种生物的数量、人口数量等社会经济指标、某种商品(例如手机)的普及率等。
logistic方程定义如下:
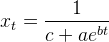 (1)
(1)
其中,t通常表示时间变量, 为模型的参数;当趋势比较完整时 a>0 b<0 c>0;其曲线如图1所示:
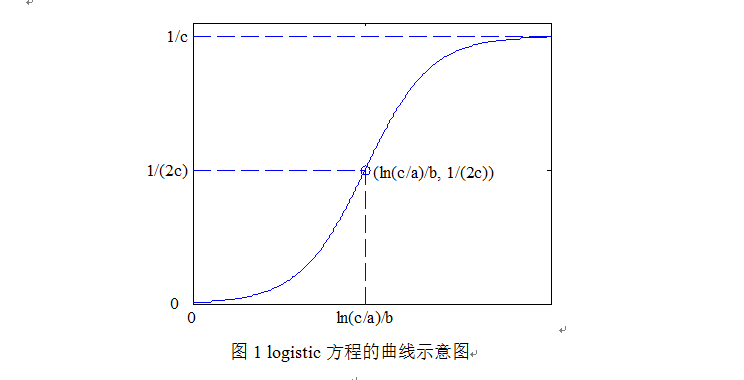
根据1图和(1)方程式得:当
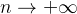 时,
时,
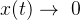 ;当
;当
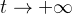 时,
时,
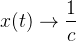 。为了研究Logistic曲线的增长特性,对(1)式求导一阶导数得:
。为了研究Logistic曲线的增长特性,对(1)式求导一阶导数得:
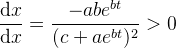
设xt(t=1, 2, …, n)为观测样本,对于logistic方程的参数,常规的估计方法有三种。
1.1、Yule算法:
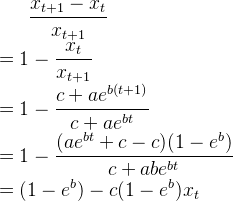 (2)
(2)
根据式(1)有
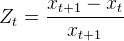 ,
,
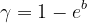 ,以及
,以及
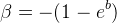 则式(2)变形为线性方程,
则式(2)变形为线性方程,
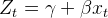 利用普通最小二乘(OLS)方法可以得到这个方程参数的估计值,b和c的估计值也可以进一步得到。
利用普通最小二乘(OLS)方法可以得到这个方程参数的估计值,b和c的估计值也可以进一步得到。
为得到a的估计值,将式(1)变形为:
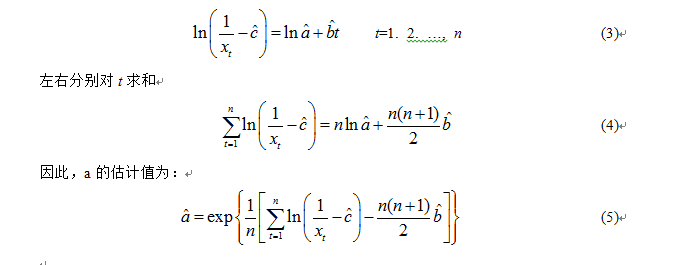
1.2、Rhodes算法:
根据式(1),有
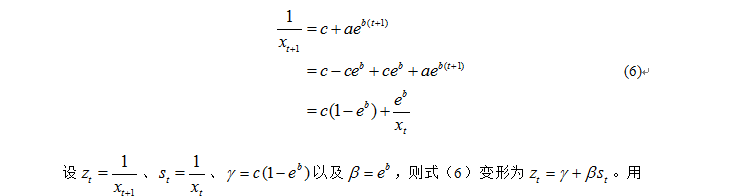
普通最小二乘(OLS)方法得到这个方程参数的估计值,并进一步得到b和c的估计值,然后利用式(3)-式(5)的方法得到a的估计值
1.3、Nair算法:
(2)式可以进一步写为:
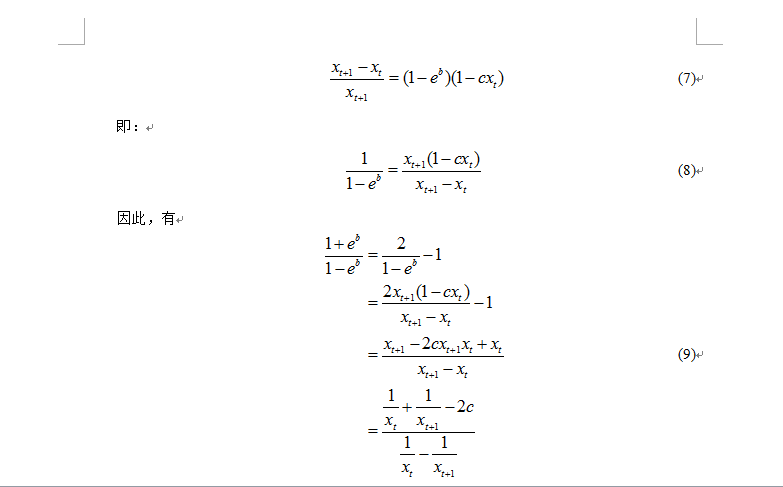

2.、matlab算法实现
中国1965-2011年CO2排放量(单位:亿吨)如表1所示:(备注:这是上课老师给的数据)
表1中国1965-2011年CO2排放量
1965
1966
1967
1968
1969
1970
1971
1972
1973
1974
480.9
522.0
468.8
469.5
573.8
737.8
869.8
933.7
977.2
997.7
1975
1976
1977
1978
1979
1980
1981
1982
1983
1984
1120.3
1176.1
1284.8
1422.1
1462.1
1499.7
1473.1
1539.2
1637.0
1771.0
1985
1986
1987
1988
1989
1990
1991
1992
1993
1994
1886.5
1994.6
2145.7
2292.0
2396.8
2387.0
2484.4
2580.8
2750.2
2915.7
1995
1996
1997
1998
1999
2000
2001
2002
2003
2004
3163.8
3231.9
3319.5
3319.6
3484.0
3550.6
3613.9
3833.1
4471.2
5283.0
2005
2006
2007
2008
2009
2010
2011
5803.2
6415.5
6797.9
7033.5
7636.3
8209.8
8979.1
用logistic方程模拟我国CO2排放量的变化趋势,分别用三种方法估计方程参数,并分别计算三种方法的MAPE及未来五年CO2排放量的预测结果。
2.1.Yule算法:
clear;clc;
%Yule算法
%author:zhuweijie
%E-mail:2377389590@qq.com
%date:2018-1-24
X=[480.9,522,468.8,469.5,573.8,737.8,869.8,933.7,977.2,...
997.7,1120.3,1176.1,1284.8,1422.1,1462.1,1499.7,...
1473.1,1539.2,1637,1771,1886.5,1994.6,2145.7,2292,...
2396.8,2387,2484.4,2580.8,2750.2,2915.7,3163.8,3231.9,...
3319.5,3319.6,3484.,3550.6,3613.9,3833.1,4471.2,5283,...
5803.2,6415.5,6797.9,7033.5,7636.3,8209.8,8979.1]
n=length(X)-1
for t=1:n
Z(t)=(X(t+1)-X(t))/X(t+1)
end
X1=[ones(46,1) X(1:n)']
Y=Z'
[B,Bint,r,rint,stats]=regress(Y,X1)% 最小二乘(OLS)
gamma=B(1,1)
beta=B(2,1)
b=log(1-gamma)
c=beta/(exp(b)-1)
a=exp((sum(log(1./X(1:n)-c))-n*(n+1)*b/2)/n)
XX=1965:2016
YY=1./(c+a*exp(b*([XX-1965])))
plot(XX,YY,'r-o')
hold on
plot(XX(1:length(X)),X,'g-^')
legend('预测值','实际值')
xlabel('年份');ylabel('CO_{2}排放量');
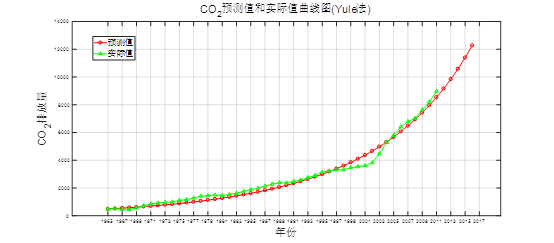
title('CO_{2}预测值和实际值曲线图(Yule法)')
set(gca,'XTick',[1965:2:2017])
grid on
format short;
forecast=YY(end-4:end)%CO2排放量的预测结果
MAPE=sum(abs(YY(1:n+1)-X)./X)/length(X)%平均相对差值
a,b,c
2.2.Rhodes算法:
clear;clc;
%Rhodes算法:
%author:zhuweijie
%E-mail:2377389590@qq.com
%date:2018-1-24
X=[480.9,522,468.8,469.5,573.8,737.8,869.8,933.7,977.2,...
997.7,1120.3,1176.1,1284.8,1422.1,1462.1,1499.7,...
1473.1,1539.2,1637,1771,1886.5,1994.6,2145.7,2292,...
2396.8,2387,2484.4,2580.8,2750.2,2915.7,3163.8,3231.9,...
3319.5,3319.6,3484.,3550.6,3613.9,3833.1,4471.2,5283,...
5803.2,6415.5,6797.9,7033.5,7636.3,8209.8,8979.1]
n=length(X)-1
for t=1:n
Z(t)=1/X(t+1)
S(t)=1/X(t)
end
X1=[ones(46,1) S(1:n)']
Y=Z'
[B,Bint,r,rint,stats]=regress(Y,X1)% 最小二乘(OLS)
gamma=B(1,1)
beta=B(2,1)
b=log(beta)
c=gamma/(1-exp(b))
a=exp((sum(log(1./X(1:n+1)-c))-(n+1)*(n+2)*b/2)/(n+1))
XX=1965:2016
YY=1./(c+a*exp(b*([XX-1965])))
plot(XX,YY,'r-o')
hold on
plot(XX(1:length(X)),X,'k-^')
set(gca,'XTick',[1965:2:2017])
legend('预测值','实际值')
xlabel('年份');ylabel('CO_{2}排放量');
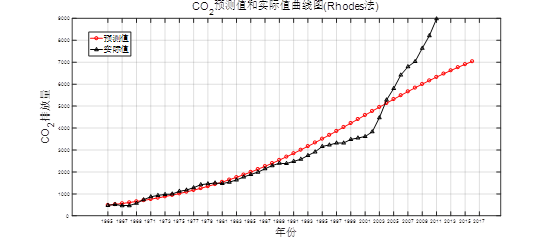
title('CO_{2}预测值和实际值曲线图(Rhodes法)')
grid on
format short;
forecast=YY(end-4:end)%CO2排放量的预测结果
MAPE=sum(abs(YY(1:n+1)-X)./X)/length(X)%平均相对差值
a,b,c
2.3.Nair算法:
clear;clc;
%Nair算法
%author:zhuweijie
%E-mail:2377389590@qq.com
%date:2018-1-24
X=[480.9,522,468.8,469.5,573.8,737.8,869.8,933.7,977.2,...
997.7,1120.3,1176.1,1284.8,1422.1,1462.1,1499.7,...
1473.1,1539.2,1637,1771,1886.5,1994.6,2145.7,2292,...
2396.8,2387,2484.4,2580.8,2750.2,2915.7,3163.8,3231.9,...
3319.5,3319.6,3484.,3550.6,3613.9,3833.1,4471.2,5283,...
5803.2,6415.5,6797.9,7033.5,7636.3,8209.8,8979.1]
n=length(X)-1
for t=1:n
Z(t)=1/X(t)-1/X(t+1)
S(t)=1/X(t)+1/X(t+1)
end
X1=[ones(46,1) S(1:n)']
Y=Z'
[B,Bint,r,rint,stats]=regress(Y,X1)% 最小二乘(OLS)
gamma=B(1,1)
beta=B(2,1)
b=log((1-beta)/(1+beta))
c=gamma*(1+exp(b))/(2*(exp(b)-1))
a=exp((sum(log(1./X(1:n)-c))-n*(n+1)*b/2)/n)
XX=1965:2016
YY=1./(c+a*exp(b*([XX-1965])))
plot(XX,YY,'r-o')
hold on
plot(XX(1:length(X)),X,'g-^')
legend('预测值','实际值')
xlabel('年份');ylabel('二氧化碳排放量');
title('二氧化碳预测值和实际值曲线图(Nair法)')
set(gca,'XTick',[1965:2:2017])
grid on
format short;
forecast=YY(end-4:end)%CO2排放量的预测结果
MAPE=sum(abs(YY(1:n+1)-X)./X)/length(X)%平均相对差值
a,b,c
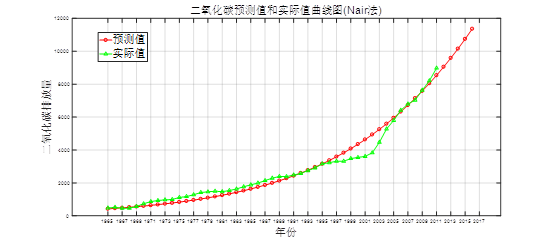
根据编程计算,三种方法参数估计的结果及MAPE如表1所示:
三种方法的参数估计结果及误差分析结果
a
b
c
MAPE
Yule算法
0.0020
-0.0580
-0.000024579
0.1141
Rhodes算法
0.0019
-0.0802
0.00010960
0.1259
Nair算法
0.0023
-0.0683
0.000016564
0.1271
三种方法对未来五年CO2排放量的预测结果(单位:百万吨)如表2所示:
中国CO2排放量的预测结果
2012
2013
2014
2015
2016
Yule算法
9167
9847
10587
11396
12282
Rhodes算法
6476.7
6624.9
6767.8
6905.3
7037.3
Nair算法
9050
9588
10152
10742
11359
如果想要最原始的文件和代码可以查看我上传的资源,源码下载地址
转载请备注
欢迎加群:707914447


最后
以上就是调皮小松鼠最近收集整理的关于matlab数学公式迭代计算,Logistic三种迭代算法公式推导及matlab代码实现的全部内容,更多相关matlab数学公式迭代计算内容请搜索靠谱客的其他文章。








发表评论 取消回复