数字逻辑设计基础（何建新）第三章

三大逻辑运算符
与逻辑（逻辑乘）——串联开关模型
注意图形化表示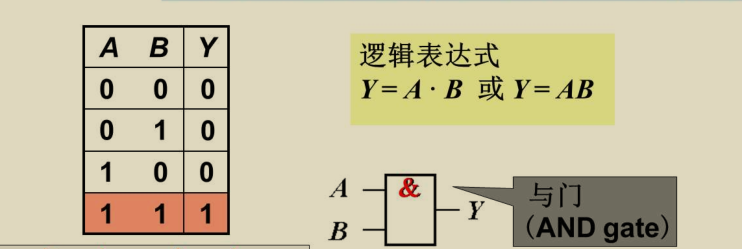

有0出0,；全1出1
或逻辑（逻辑加）——并联开关模型
注意图形化表示

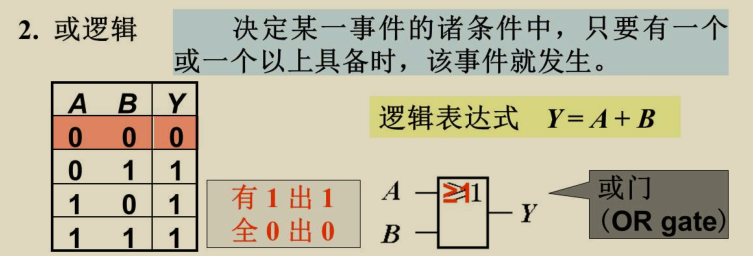
有1出1；全0出0
非逻辑（逻辑非）——短路开关模型
注意图形化表示

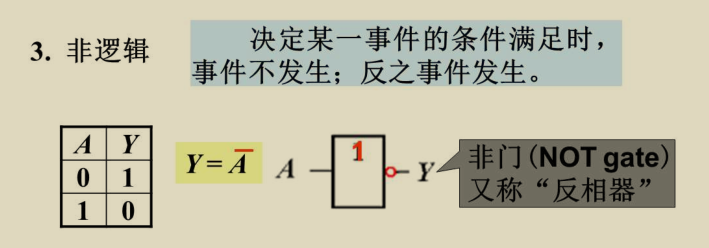
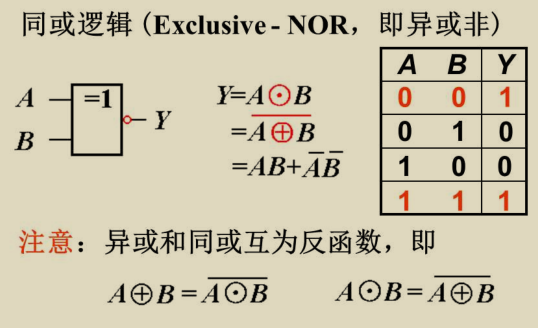
复合逻辑

若有0出1；若全1出0

若有1出0；若全0出1

若相异出1；若相同处0

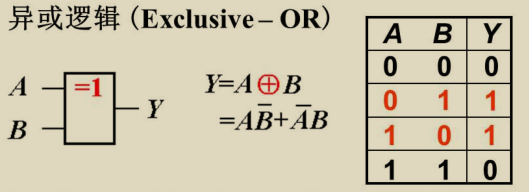
若相同出1；若相异处0

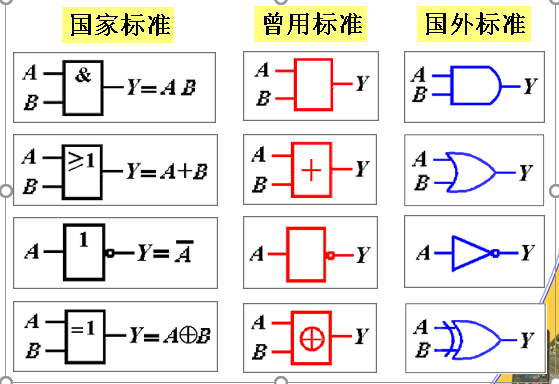
逻辑符号对照

例题：

输入信号也为0/1信号，根据异或门的规律得出结果

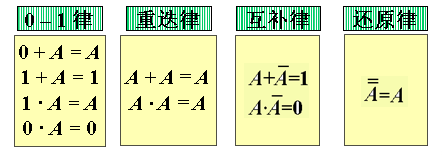
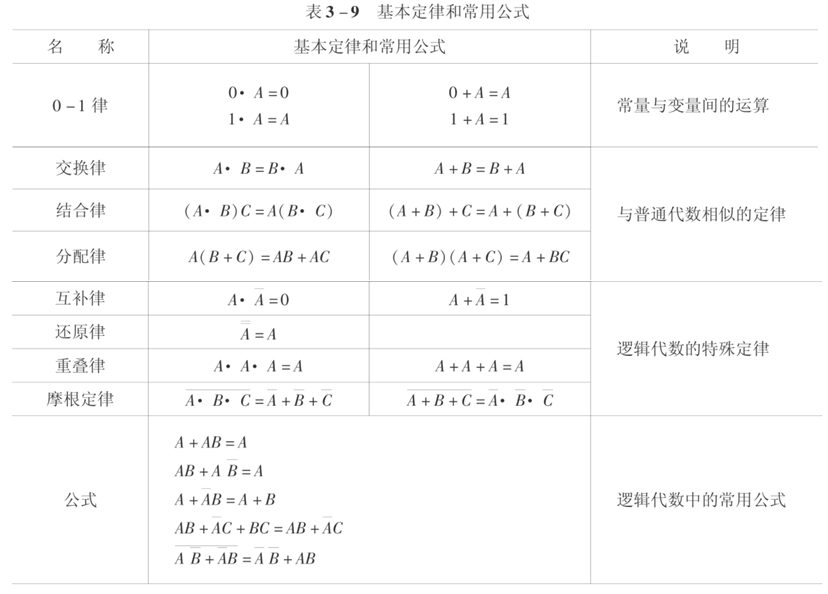
逻辑代数基本定理
逻辑常量运算公式

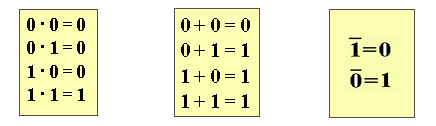
逻辑变量与常量的运算公式

三大定律
交换律
A + B = B + A
A · B = B · A
结合律
(A + B) + C = A + (B + C)
(A · B) · C = A · (B · C)
分配律
A (B + C) = AB + AC
A + BC = (A + B) (A + C)
常用公式
吸收律

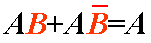
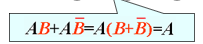
推广公式

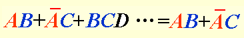
摩根定律

推广公式

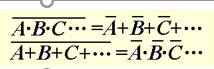
常用公式

逻辑函数的表示

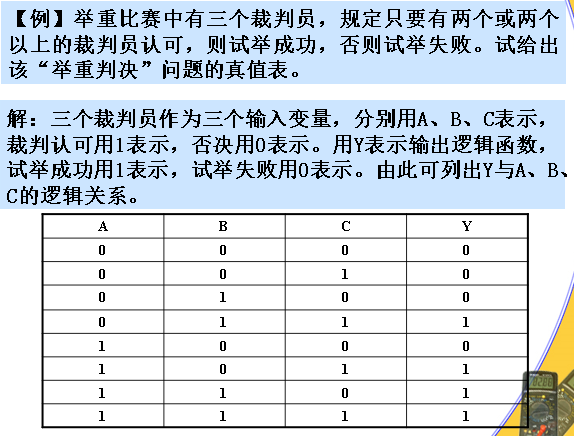
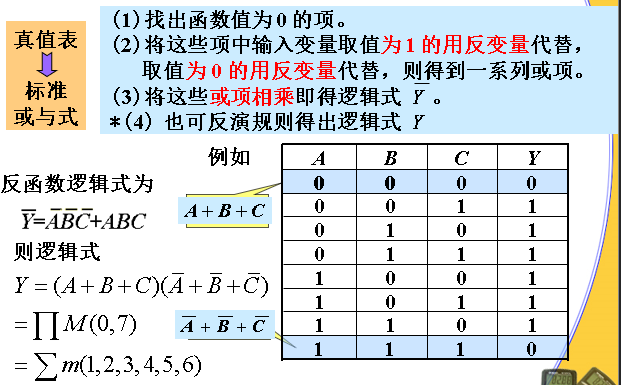
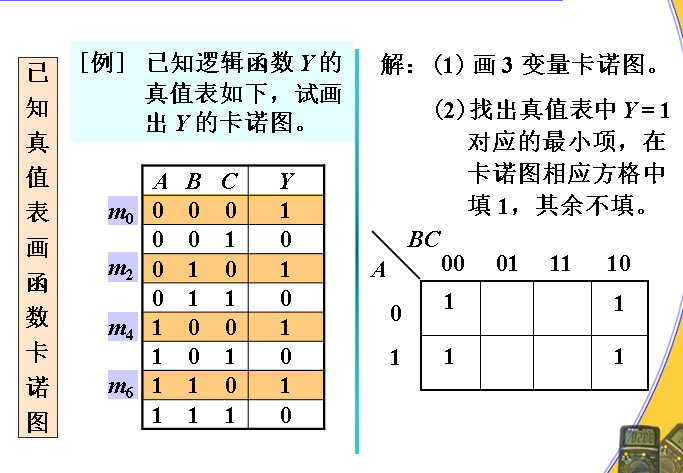
真值表
真值表以表格的形式描述所有变量的取值组合与对应的逻辑函数值
真值表可看作由左右两栏组成，左栏列出所有变量的取值组合，右栏列出变量取值组合对应的逻辑函数值
例：

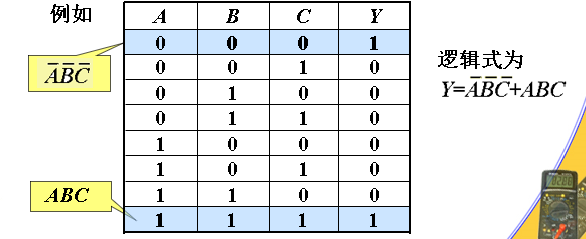
逻辑代数式
用与、或、非等基本逻辑运算表示输入与输出之间关系的表达式称为逻辑代数式，简称逻辑式

例：

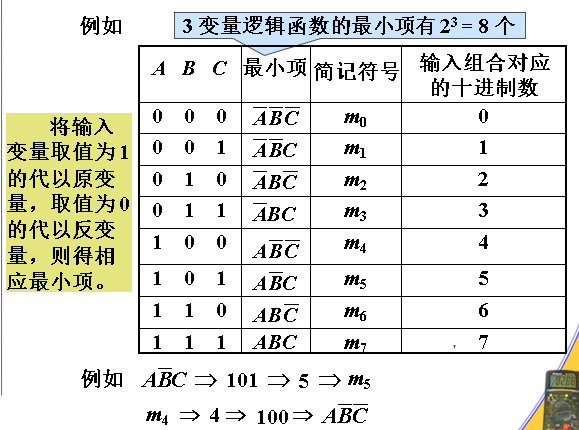
最小项表达式
n 个变量有 2^n 种组合，可对应写出 2^n 个乘积项，这些乘积项均具有下列特点：包含全部变量，且每个变量在该乘积项中 (以原变量或反变量)只出现一次。这样的乘积项称为这 n 个变量的最小项，也称为 n 变量逻辑函数的最小项
例：

最小项的基本性质
对任意一最小项，只有一组变量取值使它的值为1，而其余各种变量取值均使其值为0
不同的最小项，使其值为1 的那组变量取值也不同
对于变量的任一组取值，任意两个最小项的乘积为0
对于变量的任一组取值，全体最小项的和为1
例：

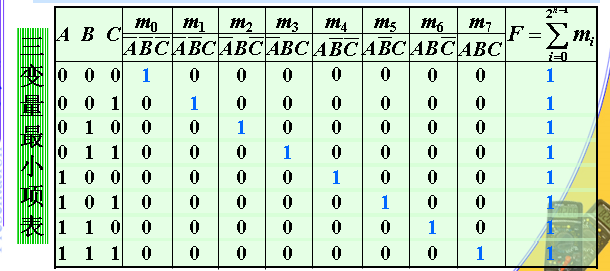
最小项编号
最小项用m表示，通常用十进制数作最小项的下标编号。把最小项中的原变量当作1，反变量当作0，所得的二进制数所对应的十进制数即为最小项的编号
最小项表达式
若干最小项之和构成最小项表达式（也叫标准与-或）

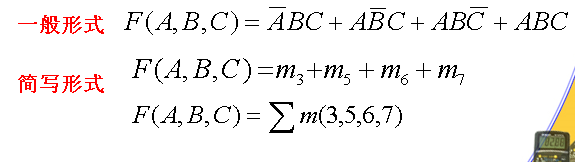
最大项表示式
最大项的定义和编号
n 个变量有 2^n 种组合，可对应写出 2^n 个相加项，这些相加项均具有下列特点：包含全部变量，且每个变量在该相加项中 (以原变量或反变量)只出现一次。这样的相加项称为这 n 个变量的最大项，也称为 n 变量逻辑函数的最大项
例：

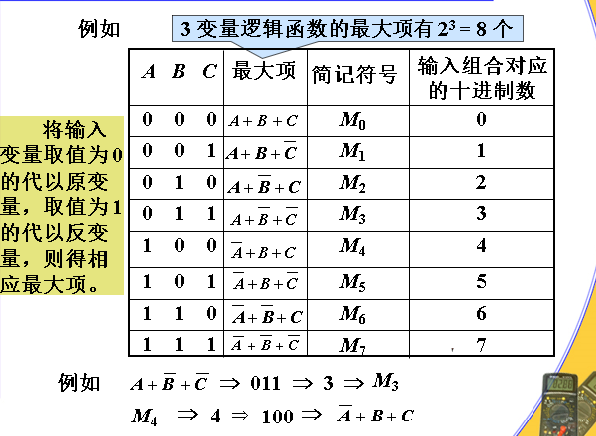
最大项的基本性质
对任意一最大项，只有一组变量取值使它的值为 0，
而其余各种变量取值均使其值为 1
不同的最大项，使其值为 0 的那组变量取值也不同
对于变量的任一组取值，任意两个最大项的相加为 1
对于变量的任一组取值，全体最大项的积为 0
最小项与最大项的关系
变量数相同时，下标号相同的最大项和最小项互补
例：

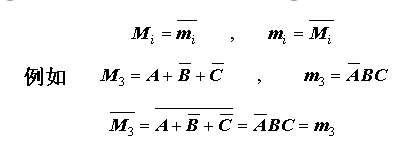
逻辑函数的标准或与式
每一个或项都是最大项的或与逻辑式称为标准或与式，又称最大项表达式

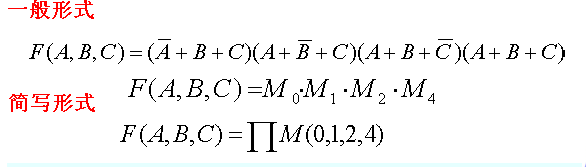
例：

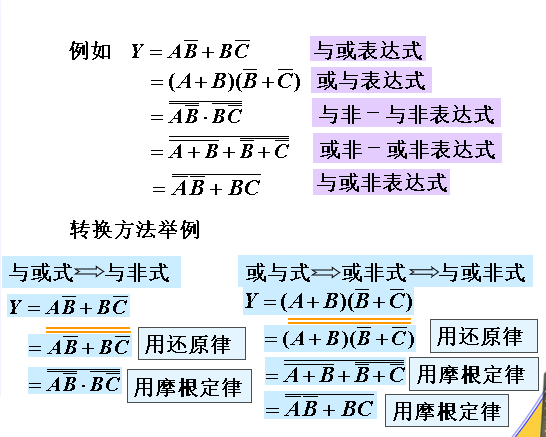
逻辑函数的非标准式
同一个逻辑函数除了用标准与或式和标准或与式描述外，还可以用其它类型的逻辑式描述(统称非标准式)
常见的非标准式有与或式、或与式、与非与非式、或非或非式、与或非式
例：

卡诺图

卡诺图的标准形式
相邻最小项
两个最小项中只有一个变量互为反变量，其余变量均相同，称为相邻最小项，简称相邻项。
相邻最小项重要特点
两个相邻最小项相加可合并为一项。消去互反变量，化简为相同变量相与
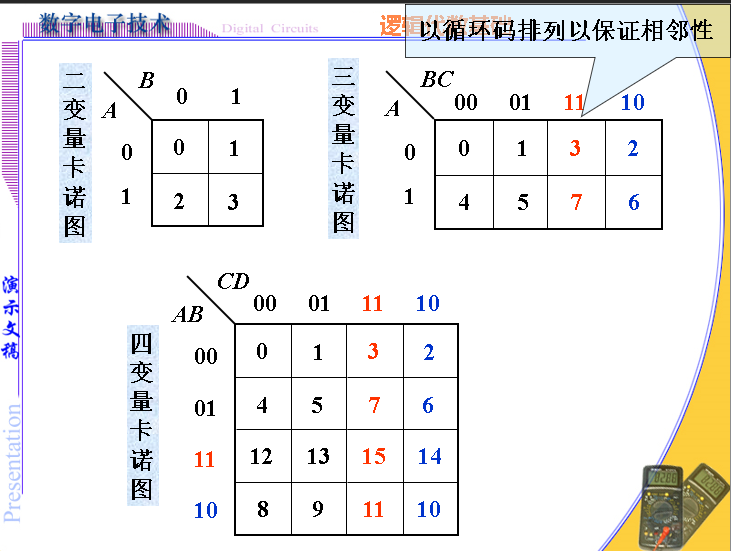
变量卡诺图
将 n 变量的 2^n 个最小项用 2^n 个小方格表示，并且使相邻最小项在几何位置上也相邻且循环相邻，这样排列得到的方格图称为 n 变量最小项卡诺图， 简称为变量卡诺图。
例：

卡诺图表示逻辑函数
例：

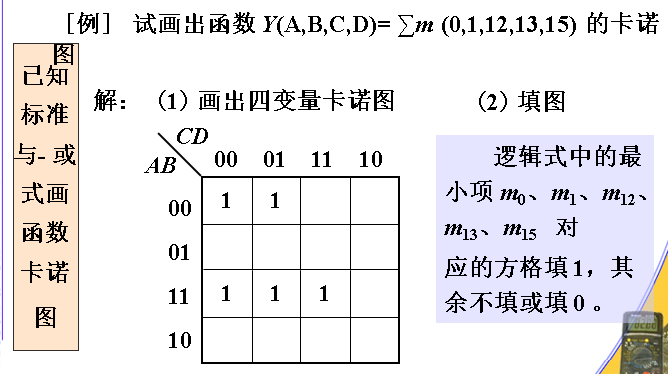
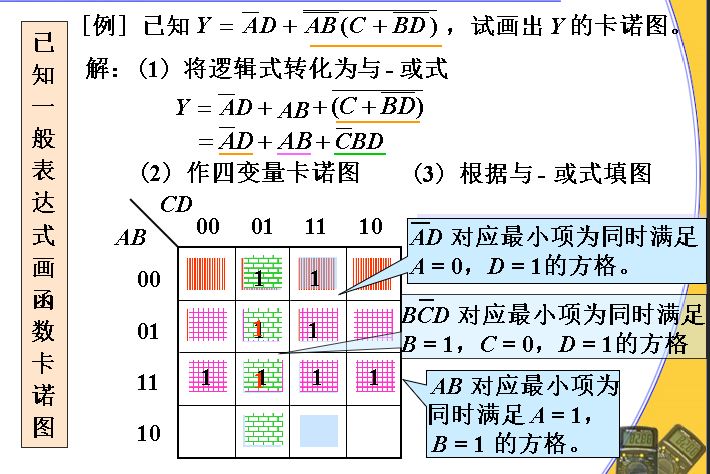
重要规则
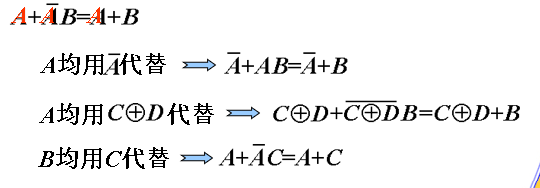
代入规则
将逻辑等式两边的某一变量均用同一个逻辑函数替代，等式仍然成立。

如果逻辑函数为编号表示的标准最小项或最大项表达式，一般不采用反演规则求反函数。
可根据最小项与最大项的互补关系，若原函数为标准的最小项表达式，对应反函数采用标准的最大项表达式，则反函数中的最大项编号就是原函数中的最小项编号；
例：

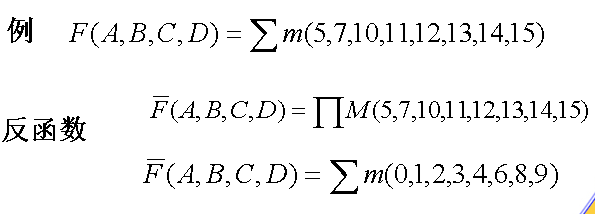
对偶规则
对任一个逻辑函数式Y，将“·”换成“+”，“+”换成“·”，“0”换成“1”，“1”换成“0”，则得到原逻辑函数式的对偶式Y ¢。
对偶规则：两个函数式相等，则它们的对偶式也相等。
变换时注意：
变量不改变
不能改变原来的运算顺序
例：

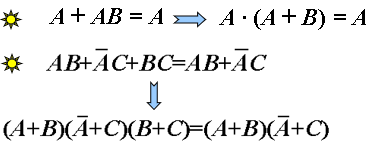
逻辑函数的化简方法

不同形式逻辑式有不同的最简式，一般先求取最简与 - 或式，然后通过变换得到所需最简式
最简与 - 或式标准
乘积项(即与项)的个数最少
每个乘积项中的变量数最少
用与门个数最少，与门的输入端数最少
最简与非式标准
非号个数最少
每个非号中的变量数最少
用与非门个数最少，与非门的输入端数最少
最简或 -与式标准
相加项(即或项)的个数最少
每个相加项中的变量数最少
用或门个数最少，或门的输入端数最少

公式化简法
并项法

例：

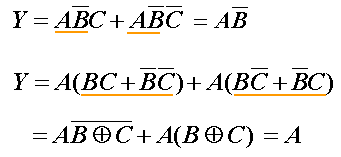
吸收法

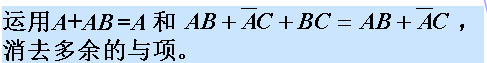
例：

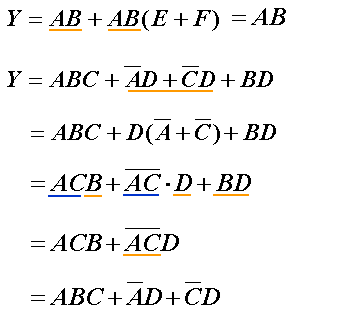
消去法

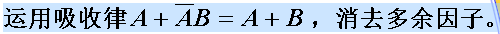
例：

配项法

例：

例：

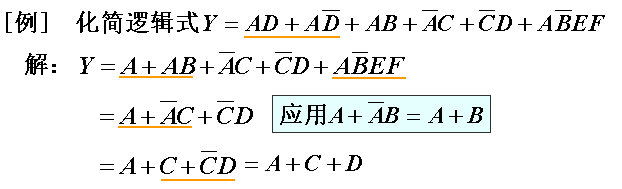
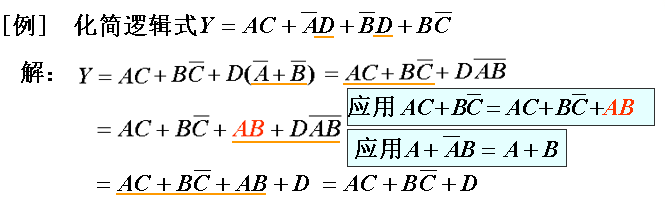
逻辑函数的化简
例：

卡诺图化简法
代数化简法与卡诺图化简法的特点

化简规则
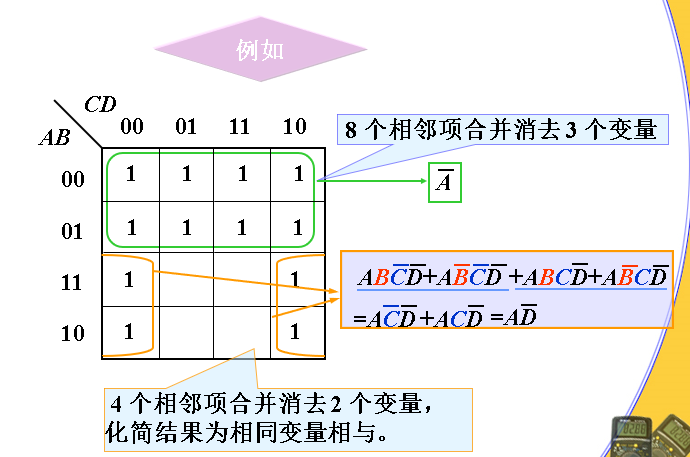
2 个相邻最小项有 1 个变量相异，相加可以消去这 1个变量，化简结果为相同变量的与；
4个相邻最小项有 2 个变量相异，相加可以消去这 2个变量，化简结果为相同变量的与；
8 个相邻最小项有 3 个变量相异，相加可以消去这 3 个变量，化简结果为相同变量的与；
2^n 个相邻最小项有 n 个变量相异，相加可以消去这 n 个变量，化简结果为相同变量的与。
例：

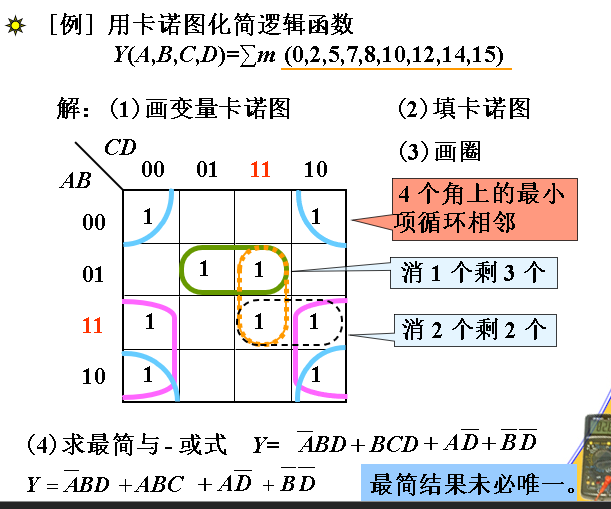
卡诺 图化简法步骤
画函数卡诺图 对填 1 的相邻最小项方格画包围圈 将各圈分别化简将各圈化简结果逻辑加
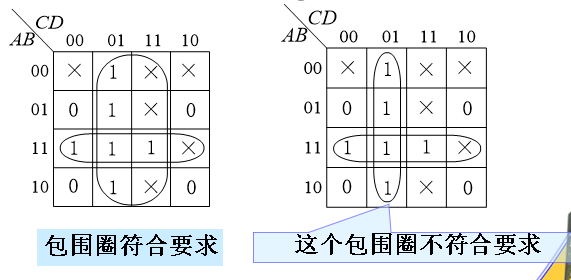
画包围圈规则
包围圈必须包含 2n 个相邻 1 方格，且必须成方形。先圈小再圈大，圈越大越是好；1 方格可重复圈，但须每圈有新 1；每个“1”格须圈到，孤立项也不能掉。
注意：
同一列最上边和最下边循环相邻，可画圈；
同一行最左边和最右边循环相邻，可画圈；
四个角上的 1 方格也循环相邻，可画圈。
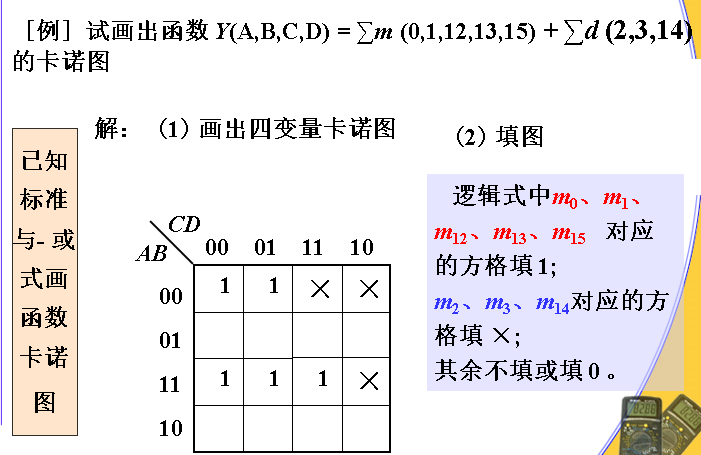
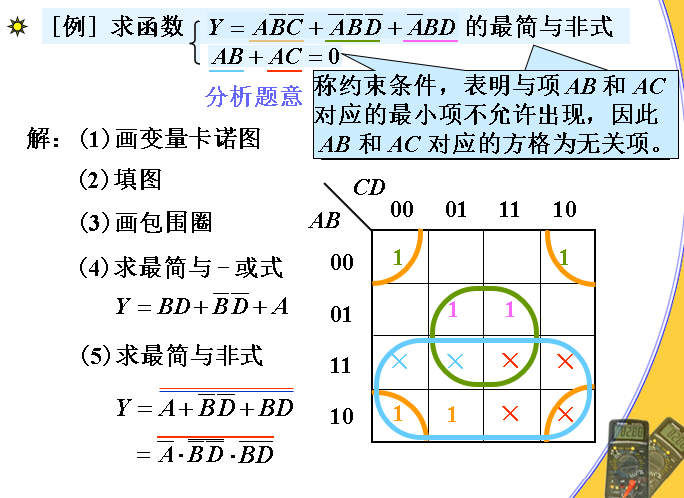
卡诺图中含无关项方格的处理原则
无关项的取值对逻辑函数值没有影响。为了使卡诺图中相邻1方格画包围圈个数最少而且包围圈中相邻1方格的个数最多，卡诺图中的无关项方格应视需要可将无关项方格看作1方格或0方格。
例：

最后

以上就是甜美草莓为你收集整理的数字逻辑设计基础（何建新）第三章的全部内容，希望文章能够帮你解决数字逻辑设计基础（何建新）第三章所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。