1,定义
z函数存储字符串s(长度n,下标从0开始)与其所有后缀s[i,n-1](0<=i<=n-1)的最大公共前缀LCP的值(一般默认z[0]=0,有时是n)
2,思路
叫他扩展KMP是有原因的,因为思想相近,我们求取z[i],尝试利用前面求取过的z函数,通过作图我们发现,当我们维持一个区间(匹配段)[L,R],使得s[0,h]==s[L,R](h==R-L+1),我们让指针i从0到n-1遍历,不断维持[L,R](当然,L<=i,初始L=R=0,并且尽可能让r大(因为l一定小于i,我们让r大就可以)
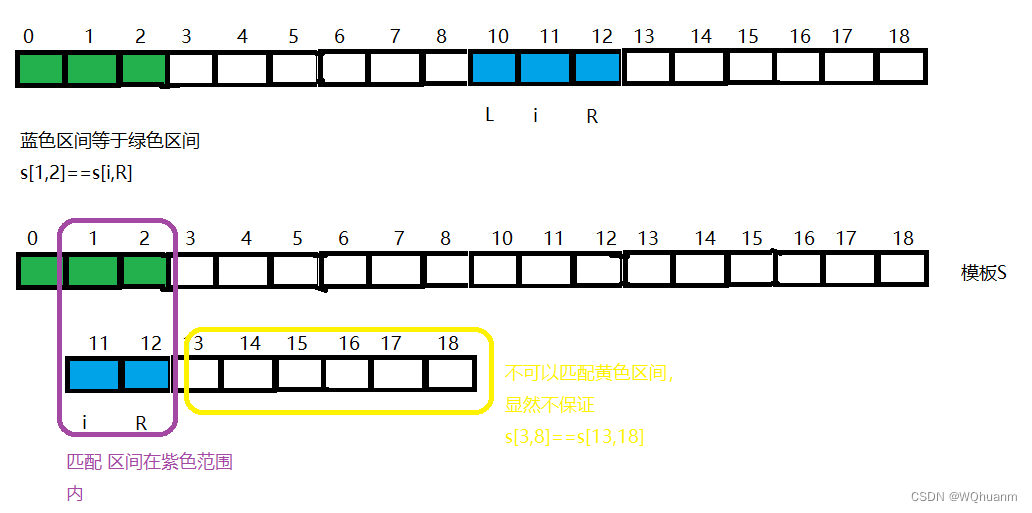
1,发现当i<=r时,s[i,R]==s[i-L,R-L],所以此时求z[i],等价于求模板s与后缀s[i-L,R-L]的LCP,即z[i]=z[i-L](当然,前提是z[i-L]<R-L+1,匹配区间不可以超出(图中黄色字))。
2,那么超出区间的话,我们只能先让z[i]=R-L+1,然后暴力比较后面部分。
3,如果i>r,无法取巧,也只能暴力
得到简洁代码
const int N = 2e5 + 100;
char s[N];
ll z[N];
int main()
{
scanf("%s", s);//长字符串用scanf,否则cin容易被tle(除非解绑了cin)
int len = strlen(s);
z[0] = 0;//默认z[0]=0
for (int i = 1, l = 0, r = 0; i < len; ++i)//i从下标1开始,因为0是规定的,初始l=r=0
{
if (i <= r && s[i - l] < r - i + 1)z[i] = z[i - l];//情况一,i<=r并且不超过区间(等于也不可以,因为刚刚好等于,不确定r的下一位是否相等,没有判断),可以直接继承z[i-l]
else
{
z[i] = max(0, r - i + 1);//取0,说明i>r,取r-i+1,说明超出匹配区间
while (i + z[i] < len && s[z[i]] == s[i + z[i]])++z[i];//暴力匹配后面部分
}
if (i + z[i] - 1 > r)l = i, r = i + z[i] - 1;//尽量让r大,有就更新r(还有l)
}
return 0;
}3,复杂度O(n)
首先i线性n,里面while观察到,最多进行n次,因为每次都会让r增大,而r小于n
4,模板题:P5410 【模板】扩展 KMP(Z 函数)
思路:
b的z函数,无脑写就是
a关于模板b的在函数,适当修改即可
#include <bits/stdc++.h>
using namespace std;
#define ll long long
typedef unsigned long long ull;
typedef pair<long long, long long> pll;
const int INF = 0x3f3f3f3f;
const int N = 2e7 + 10;
char a[N], b[N];
ll a1[N], b1[N];
int main()
{
scanf("%s%s", a, b);
int la = strlen(a), lb = strlen(b);
//a对模板b,取z[i-l],取的是模板部分的z函数,所以我们先求出b的z函数
b1[0] = lb;//这题规定z[0]=n
for (int i = 1, l = 0, r = 0; i < lb; ++i)
{
if (i <= r && b1[i - l] < r - i + 1)b1[i] = b1[i - l];
else
{
b1[i] = max(0, r - i + 1);
while (b1[i] + i < lb && b[b1[i]] == b[i + b1[i]])++b1[i];
}
if (b1[i] + i - 1 > r)l = i, r = i + b1[i] - 1;
}
//暴力找a关于模板b的z[0]
for (int i = 0; i < la; ++i)
{
if (b[i] == a[i])++a1[0];
else break;//不等于直接跳出,不能待着
}
for (int i = 1, l = 0, r = 0; i < la; ++i)
{
if (i <= r && b1[i - l] < r - i + 1)a1[i] = b1[i - l];//注意,a对模板b,取z[i-l],取的是模板部分的z函数,所以是判断b的z函数的值,取也是b的z函数的值
else
{
a1[i] = max(0, r - i + 1);
while (i + a1[i] < la && b[a1[i]] == a[i + a1[i]])++a1[i];
}
if (i + a1[i] - 1 > r)l = i, r = i + a1[i] - 1;
}
ll as = 0, bs = 0;
for (int i = 0; i < la; ++i)as ^= (i + 1) * (a1[i] + 1);
for (int i = 0; i < lb; ++i)bs ^= (i + 1) * (b1[i] + 1);
cout << bs << endl << as << endl;
return 0;
}
最后
以上就是内向高跟鞋最近收集整理的关于Z函数(扩展KMP) 1,定义2,思路3,复杂度O(n)4,模板题:P5410 【模板】扩展 KMP(Z 函数)的全部内容,更多相关Z函数(扩展KMP) 1,定义2,思路3,复杂度O(n)4,模板题:P5410内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复