信道

单符号离散信道

​ 信源发出X=a，经过信道，信宿出现符号b的概率：“a出现的前提下出现b的条件概率”，也就是说$P(b/a)$体现了信道对输入符号的传递作用。

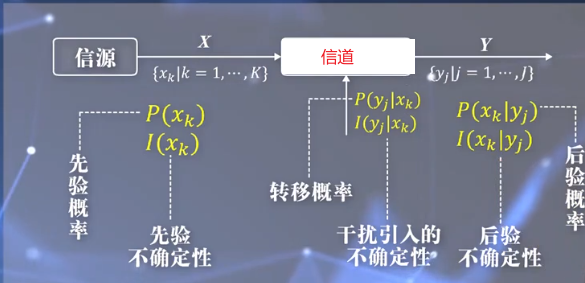
互信息（这才是信息）

​ 这里就是说，一开始信源传递a，由于信道的噪声干扰$I(b/a)$，信宿得到了b，那么互信息就是信宿得到b后对符号a的不确定性的消除。$I(a;b)=I(a)-I(a/b)=I(b)-I(b/a)$。

​ 可以为负值，当b拥有一种误导性质的时候，增大了a的不确定性。

平均交互信息量

​ 互信息只能表达信道上传递一个具体符号所传输的信息量，而平均交互信息量$I(X;Y)=I(Y;X)=H(X)-H(X/Y)$

​ 非负性：大于等于0，当且仅当X,Y独立的时候等号成立。

​ 极值性：小于等于H(X)，这就是说从信宿Y中获取关于信源X的信息量不会超过信源X本身含有的信息量 。

损失熵，疑义度

$H(X/Y)$

噪声熵，散布度

$H(Y/X)$

归并无噪信道（从发送端考虑）

​ 损失熵=0，$H(Y/X)=0$。就是说信源发出一个a，信宿接收的一定是b（不论b和a相差多少）。$I(X;Y)=H(Y)$。

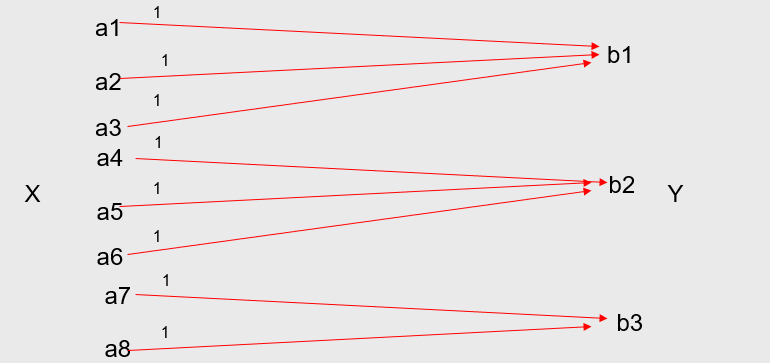
发散无损信道（从接收端考虑）

​ 疑义度=0，$H(X/Y)=0$。就是信宿接收到b，那么就可以确定信源发送的是a，没有疑义。$I(X;Y)=H(X)$。

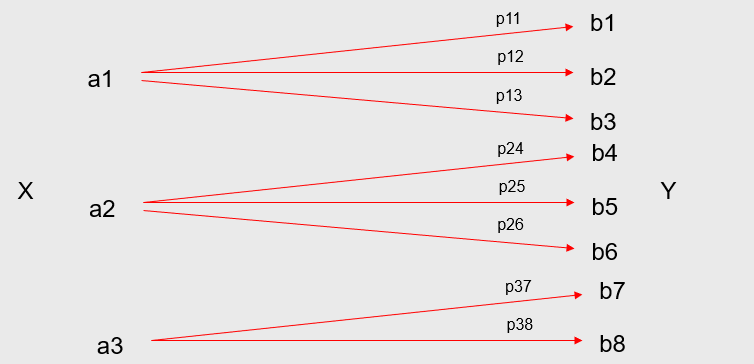
无噪无损信道

​ $\mathrm{I}(\mathrm{X};\mathrm{Y})=\mathrm{H}(\mathrm{X})=\mathrm{H}(\mathrm{Y})$，一对一。

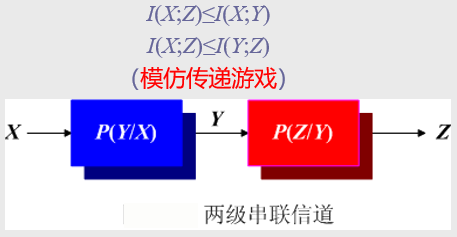
串联信道

数据处理定理

传递的信息逐级递减。

信道容量（固有的属性，与输入的信源分布无关）

​ 信道容量：传输的有效性，即一个给定信道的最大信息传输率。（信道的信息传输率＝平均互信息，即 R=I(X;Y) ，比特/符号）。

C = max ⁡ P ( X ) { I ( X ; Y ) } = max ⁡ P ( X ) { R ( X , Y ) } C=max _{P(X) }{I(X ; Y)}=max _{P(X)}{R(X, Y)} C=maxP(X)​{I(X;Y)}=maxP(X)​{R(X,Y)}，信息传输率$=I(X;Y)$

​ 单位时间的信道容量：$C_t=C/t$，也称为信道的最大信息传输速率（比特/秒，t是传递一个符号需要的时间秒）。

$I(X;Y)=H(X)-H(X/Y)=H(Y)-H(Y/X)$

匹配信源

能够使平均交互信息量达到信道容量C的信源。

几种特殊无噪信道的信道容量

无损信道：lgr，等概分布的输入信源

无噪信道：lgs，可以使输出等概分布的输入信源（很多）

最后

以上就是碧蓝睫毛膏为你收集整理的信息论3——信道（单符号离散信道，互信息，各种熵）信道的全部内容，希望文章能够帮你解决信息论3——信道（单符号离散信道，互信息，各种熵）信道所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。