数字通信第六章——信道模型和信道容量

一、信道模型

描述信道常用的三个参数：输入X；输出Y；输入与输出间的条件概率$P(y_i|x_i)$。如果$P(y|x)={\prod }_{i=1}^{m}P(y_i|x_i)$，则该信道无记忆。接下来描述四种信道模型：

1、二进制对称信道BSC

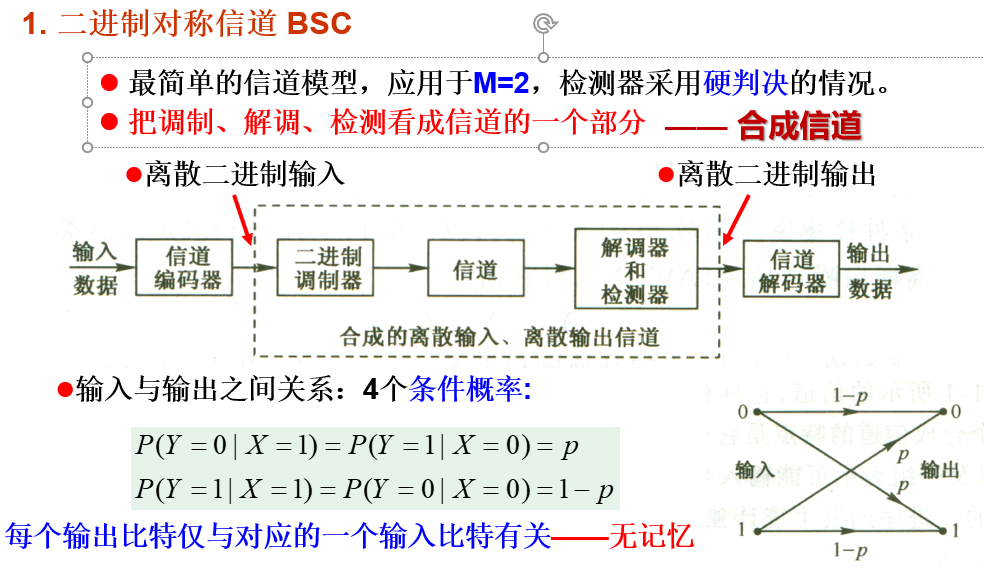
2、离散无记忆信道DMC

quad 更广义的离散输入输出的信道。输入是M元符号，输出是Q元符号。无记忆。条件概率可以写成矩阵形式。

3、离散输入、连续输出信道

quad 调制器输入信号为离散字符，检测器的输出未量化。离散输入，连续输出，比如AWGN信道，混入了噪声，导致输出连续。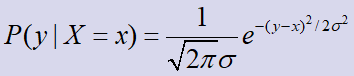

4、波形信道

quad 输入输出都是波形，都连续。矢量AWGN信道模型：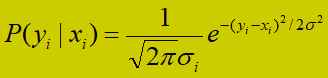

二、信道容量

对于DMC信道

信道容量为输入X与输出Y的互信息$I(X,Y)$的最大值。

对于BSC信道

选择等概的输入符号能使平均互信息最大。因此，只要令输入符号等概，就可以得出信道容量；除了选择等概以外，一般情况下，只要信道转移概率矩阵对称，就可以使 I(X, Y)最大化。

波形信道

AWGN信道在带限及平均功率受限的输入条件下信道容量——香农公式：
$$C=Wlog(1+\frac{P_{av}}{W{N}_0})$$
在AWGN信道，C与带宽W，发送功率$P_{av}$有关！

• 信道容量随SNR的增加而单调增加，$SNR=10\ast lg(\frac{P_{av}}{W{N}_0})$，$N_0$是噪声功率谱密度，$W{N}_0$是噪声功率
• 如果$P_{av}$固定，容量随带宽W的增加而增加。当W区域无穷时，信道容量趋于一个渐近值
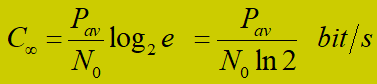
• $P_{av}=C{ϵ}_b，{ϵ}_b为每bit能量$，因此，
• 信道容量公式的意义：为在噪声信道中可靠通信确定传输速率的上限值。
• 噪声编码定理：
  只要传输速率R<C，总存在一种信道编码，以所要求的任意小的差错概率实现可靠通信；
  反之，如果R>C,不可能有任何一种编码能使差错概率趋近于零。

用正交信号可以达到信道容量极限

只要${ϵ}_b/N_0>In2$，对于正交信号，通过增加波形数M可以使差错概率$P_M$任意小。$R < C_{无穷} $时，增加正交信号数目M 可以使 $P_M$任意小,但实际得到的性能与信道容量公式算出的性能之间存在较大差距。

最后

以上就是刻苦发夹为你收集整理的数字通信第六章——信道模型和信道容量的全部内容，希望文章能够帮你解决数字通信第六章——信道模型和信道容量所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。