路径跟踪算法学习及总结
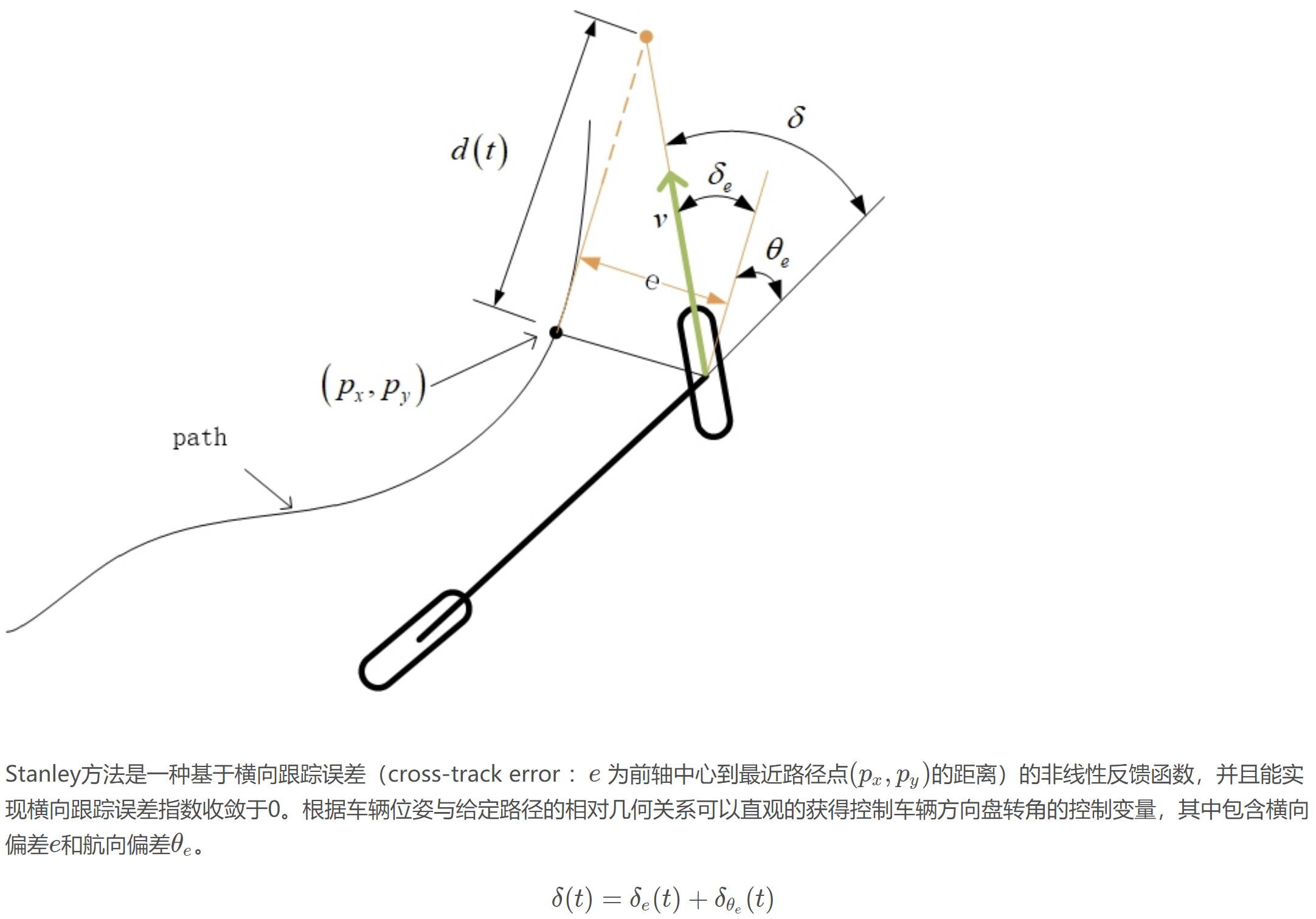
1.Stanley method 前轴控制


2.Pure pursuit(纯跟踪)
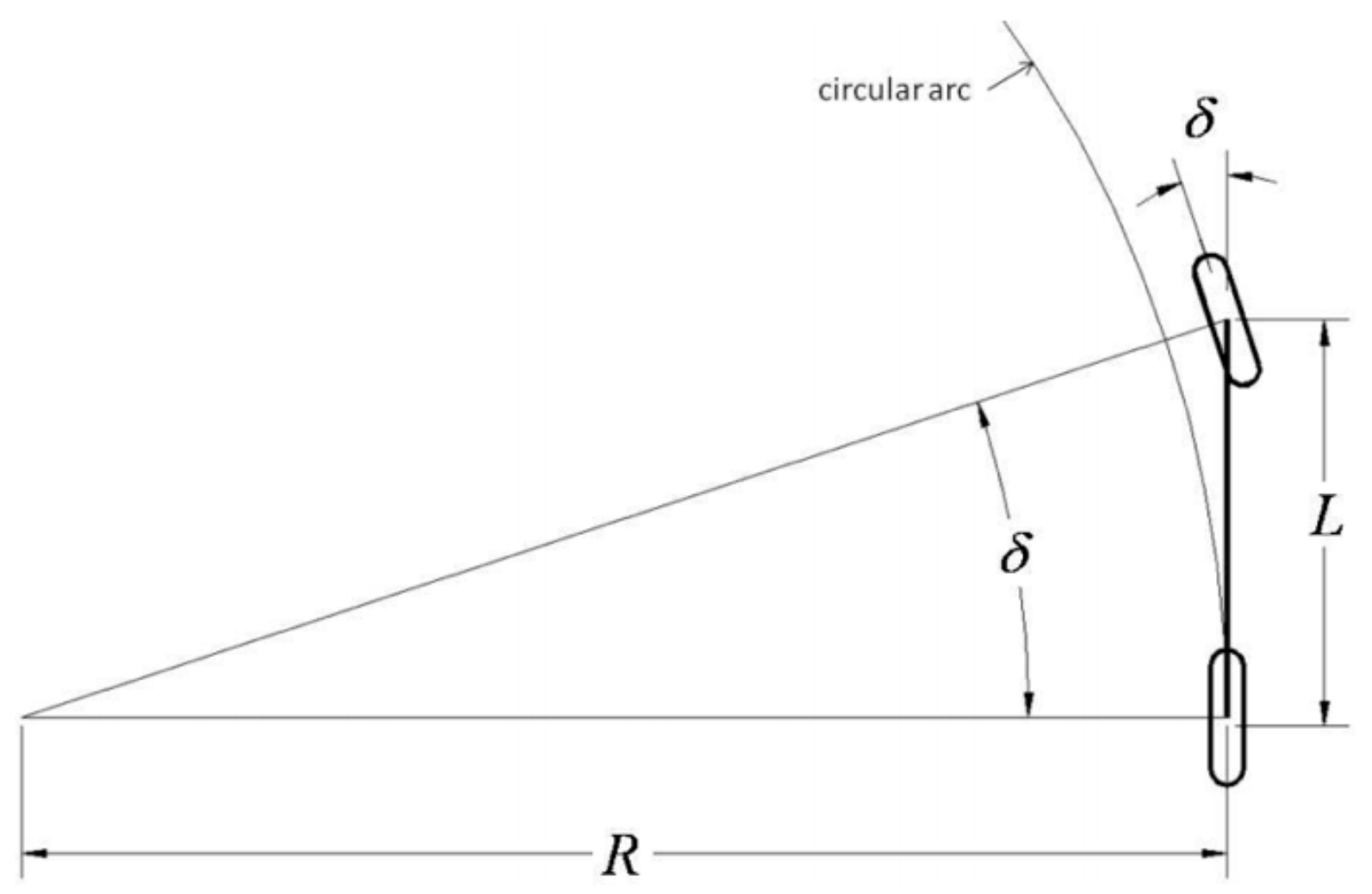
自行车模型 其中 δ 表示前轮的转角,L 为轴距(Wheelbase),R则为在给定的转向角下后轴遵循着的圆的半径。这个公式能够在较低速度的场景下对车辆运动做估计。
从自行车模型出发,纯跟踪算法以车后轴为切点, 车辆纵向车身为切线, 通过控制前轮转角,使车辆可以沿着一条经过目标路点(goal point)的圆弧行驶,如下图所示
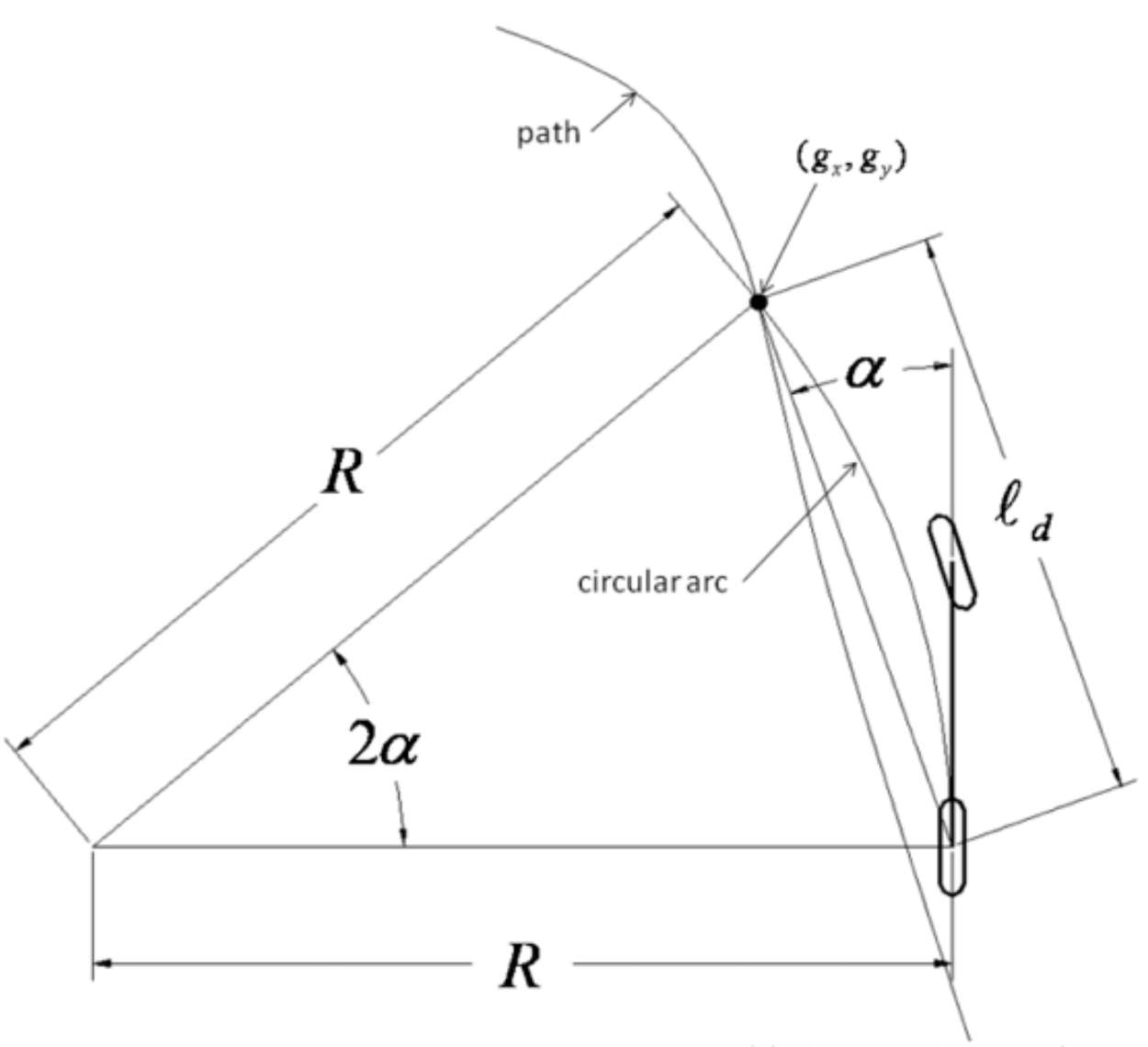
图中 (gx, gy)是我们下一个要追踪的路点,它位于我们已经规划好的全局路径上,现在需要控制车辆是的车辆的后轴经过该路点,表示车辆当前位置(即后轴位置)到目标路点的距离, 表示目前车身姿态和目标路点的夹角,那么更具正弦定理我们可以推导出如下转换式:
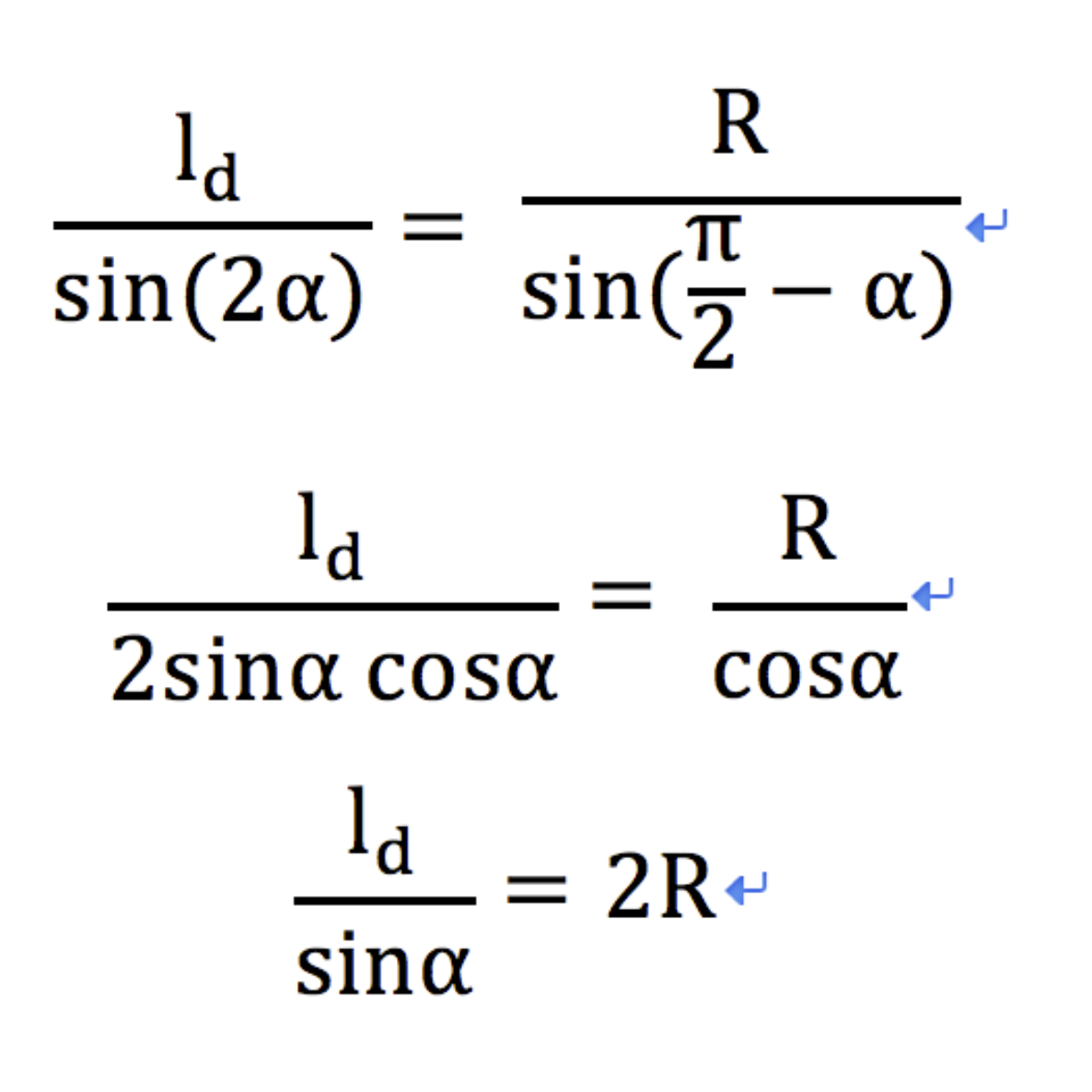
结合以上两式,我们可以得出纯追踪算法控制量的的最终表达式:
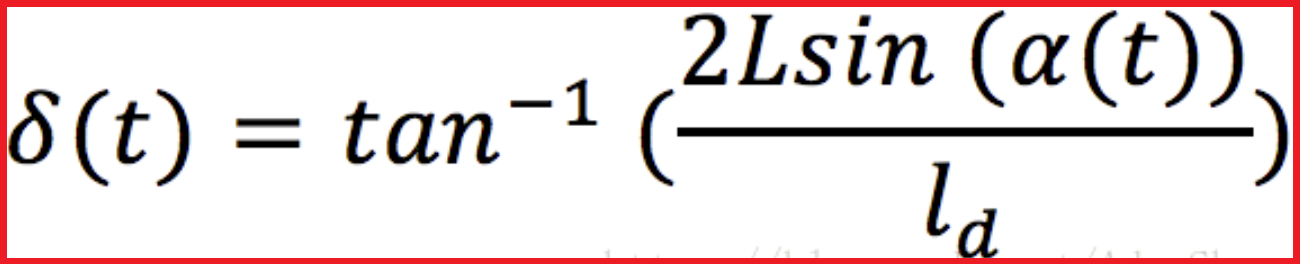
一种最常见的调整前视距离的方法就是将前视距离表示成车辆纵向速度的线形函数,即ld=kVx,那么前轮的转角公式就变成了:
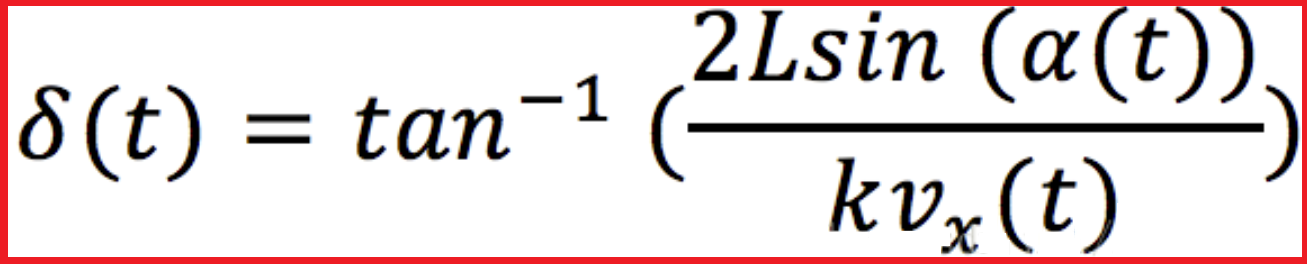
那么纯追踪控制器的调整就变成了调整系数k,通常来说,会使用最大,最小前视距离来约束前视距离,越大的前视距离意味着轨迹的追踪越平滑,小的前视距离会使得追踪更加精确(当然也会带来控制的震荡)
3.Rear_wheel_feedback 后轴控制
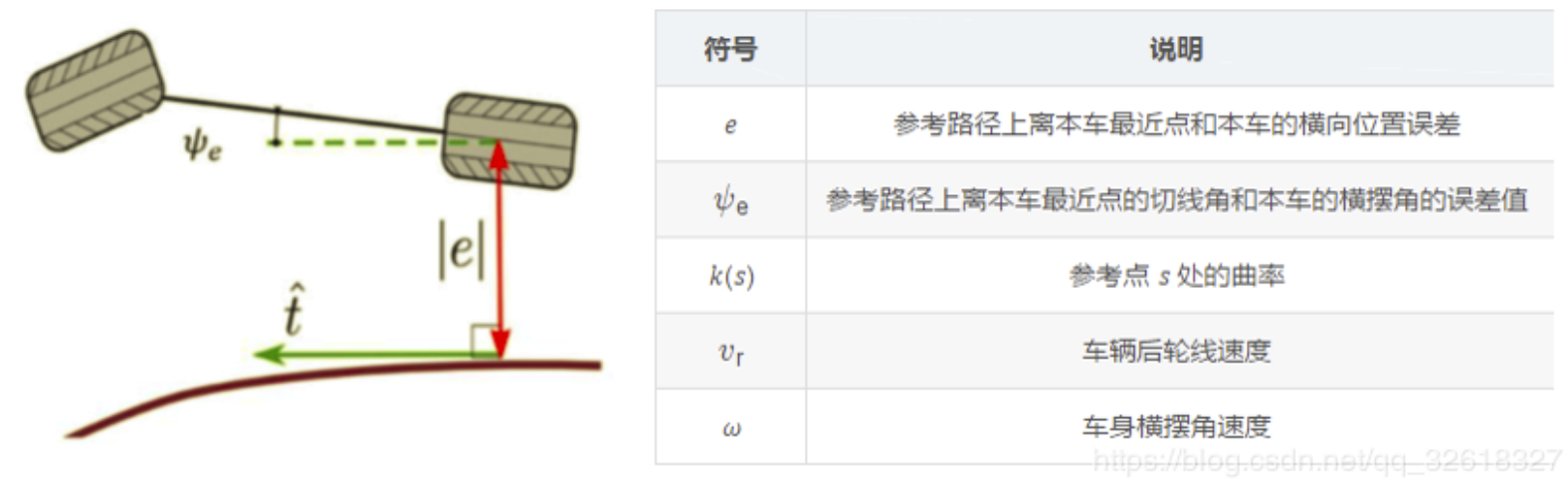
后轮反馈式(Rear wheel feedback)是利用 后轮中心 的 路径跟踪偏差量 来进行转向控制量计算的方法
根据运动学方程
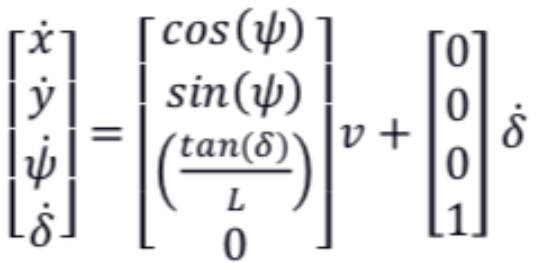
及车辆后轮与参考路径的几何关系
可推导出参考路径坐标系 (????, ????) Ferent 坐标系下 (????, ????, ψ????) 的变化率为:
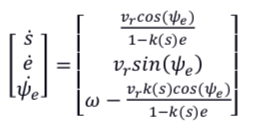
对于二次连续可导的参考线,需要设计车身横摆角速度????保证在李亚普洛夫方程下局部渐进收敛:
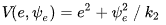
李亚普洛夫稳定(一个分析系统的稳定性方法)用数学的语言描述为:
可控可微分的状态方程 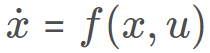
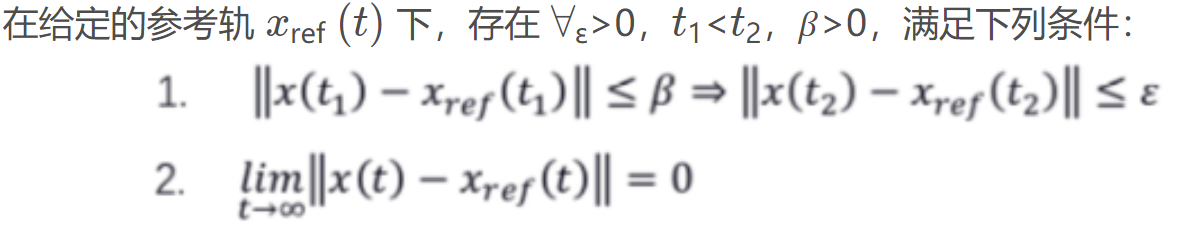 对于李亚普洛夫稳定也分为渐进稳定和指数稳定 渐进稳定指对于时变系统,????在条件(1)下独立于时间t1 指数稳定指收敛率是以指数下降
对于李亚普洛夫稳定也分为渐进稳定和指数稳定 渐进稳定指对于时变系统,????在条件(1)下独立于时间t1 指数稳定指收敛率是以指数下降
对于后轮反馈式算法,为了保证车辆的李亚普洛夫稳定性,车身横摆角速度????可表示为式
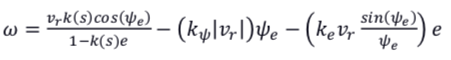
其中, ????ψ 为横摆角偏差反馈控制增益, ????e 为横向位置偏差反馈控制增益
因此,根据运动学方程,可得到前轮转角????为:
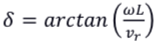
基于模型追踪的方法(待补充)
基于模型可以分为运动模型和动力学模型,控制算法可以使用LQR优化或者使用MPC。
最后
以上就是现实羽毛最近收集整理的关于路径跟踪算法学习及总结的全部内容,更多相关路径跟踪算法学习及总结内容请搜索靠谱客的其他文章。
![[运动控制算法]模型预测控制前言一、基于运动学模型的模型预测控制二、项目演示三、总结四、参考](https://www.shuijiaxian.com/files_image/reation/bcimg1.png)







发表评论 取消回复