一、PID控制
提到智能车或运动控制，最经典，最常用的就是PID控制，PID算法是一种闭环控制算法，其中PID是比例 (Proportion) 积分 ,(Integral) 微分 ,(Differential coefficient) 的缩写，分别代表了三种控制算法。
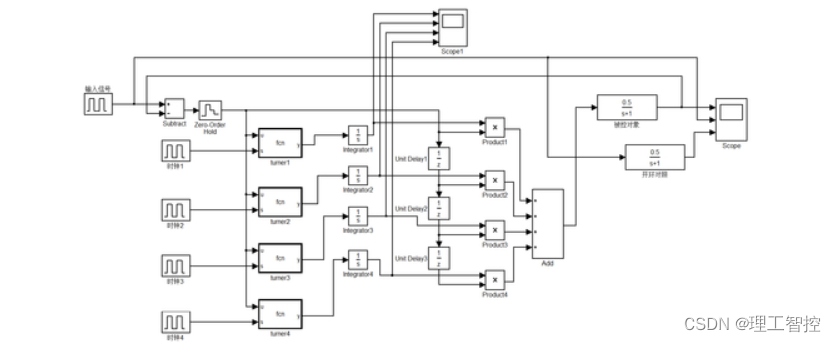
这里，使用一个过阻尼的二阶系统作为被控对象，对PID控制进行仿真测试：
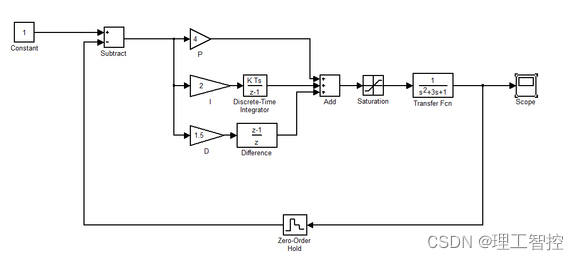
由于控制器一般为数字控制器，这里采用离散形式的PID。
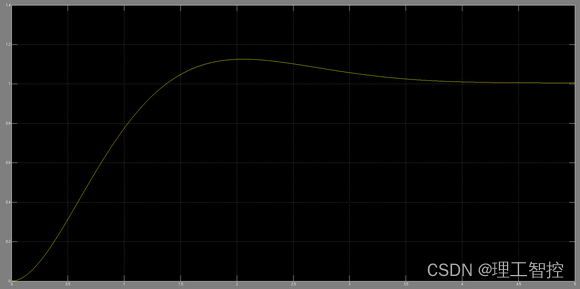
单位阶跃相应的时域信号可以利用单片机，DSP,FPGA等主控芯片强大的计算能力，对传统散式PID进行改良。常见的方法有，积分分离，微分先行，模糊PID等。
理工智控路威机器人便使用该算法作为底盘运动控制核心算法。部分代码样例如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157#include "pid.h" #define PID_SCALE 0.01f //PID缩放系数 #define PID_INTEGRAL_UP 1000 //积分上限 int16_t ax_motor_kp=200; //电机转速PID-P 比例 int16_t ax_motor_ki=0; //电机转速PID-I 积分 int16_t ax_motor_kd=400; //电机转速PID-D 微分 /** * @简 述 电机A PID控制函数 * @参 数 spd_target:编码器速度目标值 ,范围（±250） * spd_current: 编码器速度当前值 * @返回值 电机PWM速度 */ int16_t AX_PID_MotorVelocityCtlA(int16_t spd_target, int16_t spd_current) { static int16_t motor_pwm_out; static int32_t bias,bias_last,bias_integral = 0; //获得偏差值 bias = spd_target - spd_current; //计算偏差累加值 bias_integral += bias; //抗积分饱和 if(bias_integral>PID_INTEGRAL_UP)bias_integral = PID_INTEGRAL_UP; if(bias_integral<-PID_INTEGRAL_UP)bias_integral = -PID_INTEGRAL_UP; //PID计算电机输出PWM值 motor_pwm_out += ax_motor_kp*bias*PID_SCALE + ax_motor_kd*(bias-bias_last)*PID_SCALE + ax_motor_ki*bias_integral*PID_SCALE; //记录上次偏差 bias_last = bias; //限制最大输出 if(motor_pwm_out > 1950) motor_pwm_out = 1950; if(motor_pwm_out < -1950) motor_pwm_out = -1950; //返回PWM控制值 return motor_pwm_out; } /** * @简 述 电机B PID控制函数 * @参 数 spd_target:编码器速度目标值 * spd_target: 编码器速度当前值 * @返回值 电机PWM速度 */ int16_t AX_PID_MotorVelocityCtlB(int16_t spd_target, int16_t spd_current) { static int16_t motor_pwm_out; static int32_t bias,bias_last,bias_integral = 0; //获得偏差值 bias = spd_target - spd_current; //计算偏差累加值 bias_integral += bias; //抗积分饱和 if(bias_integral>PID_INTEGRAL_UP)bias_integral = PID_INTEGRAL_UP; if(bias_integral<-PID_INTEGRAL_UP)bias_integral = -PID_INTEGRAL_UP; //PID计算电机输出PWM值 motor_pwm_out += ax_motor_kp*bias*PID_SCALE + ax_motor_kd*(bias-bias_last)*PID_SCALE + ax_motor_ki*bias_integral*PID_SCALE; //记录上次偏差 bias_last = bias; //限制最大输出 if(motor_pwm_out > 1950) motor_pwm_out = 1950; if(motor_pwm_out < -1950) motor_pwm_out = -1950; //返回PWM控制值 return motor_pwm_out; } /** * @简 述 电机C PID控制函数 * @参 数 spd_target:编码器速度目标值 * spd_target: 编码器速度当前值 * @返回值 电机PWM速度 */ int16_t AX_PID_MotorVelocityCtlC(int16_t spd_target, int16_t spd_current) { static int16_t motor_pwm_out; static int32_t bias,bias_last,bias_integral = 0; //获得偏差值 bias = spd_target - spd_current; //计算偏差累加值 bias_integral += bias; //抗积分饱和 if(bias_integral>PID_INTEGRAL_UP)bias_integral = PID_INTEGRAL_UP; if(bias_integral<-PID_INTEGRAL_UP)bias_integral = -PID_INTEGRAL_UP; //PID计算电机输出PWM值 motor_pwm_out += ax_motor_kp*bias*PID_SCALE + ax_motor_kd*(bias-bias_last)*PID_SCALE + ax_motor_ki*bias_integral*PID_SCALE; //记录上次偏差 bias_last = bias; //限制最大输出 if(motor_pwm_out > 1950) motor_pwm_out = 1950; if(motor_pwm_out < -1950) motor_pwm_out = -1950; //返回PWM控制值 return motor_pwm_out; } /** * @简 述 电机D PID控制函数 * @参 数 spd_target:编码器速度目标值 * spd_target: 编码器速度当前值 * @返回值 电机PWM速度 */ int16_t AX_PID_MotorVelocityCtlD(int16_t spd_target, int16_t spd_current) { static int16_t motor_pwm_out; static int32_t bias,bias_last,bias_integral = 0; //获得偏差值 bias = spd_target - spd_current; //计算偏差累加值 bias_integral += bias; //抗积分饱和 if(bias_integral>PID_INTEGRAL_UP)bias_integral = PID_INTEGRAL_UP; if(bias_integral<-PID_INTEGRAL_UP)bias_integral = -PID_INTEGRAL_UP; //PID计算电机输出PWM值 motor_pwm_out += ax_motor_kp*bias*PID_SCALE + ax_motor_kd*(bias-bias_last)*PID_SCALE + ax_motor_ki*bias_integral*PID_SCALE; //记录上次偏差 bias_last = bias; //限制最大输出 if(motor_pwm_out > 1950) motor_pwm_out = 1950; if(motor_pwm_out < -1950) motor_pwm_out = -1950; //返回PWM控制值 return motor_pwm_out; }
二、滑模变结构控制
不同于PID控制，滑模变结构控制（Variable Structure Control, VSC）是一种非连续的控制算法，这种系统的输出值只有开关两种状态，系统通过对切换函数进行计算来做出决策，确定系统应该处于那种状态。它其实是一种非线性控制，主要特点是控制的不连续性和控制结构的可变性，这种控制是依据被控对象的状态动态调整，使得系统状态轨迹按照设计好的滑动模态运动，所以得名滑模控制。（所谓“变结构”可以初步理解为在开关两种状态之间切换）
滑模态是预先设计好的，与系统的状态和外界的扰动等都不相关，因此具有参数扰动不灵敏性和实现简单的优点，是一种鲁棒控制方法。
为方便大家理解，这里以路威机器人的电机速度环控制为例，将PID与滑模变结构控制两种控制方式进行类比：
PID算法大家应该都比较熟悉，首先当前计算误差
e[t] = r[t] - c[t]
通过当前误差于上一次误差，计算出输出量为
c[t] = Kp*e[t] + Kd*(e[t]-e[t-1])+Ki*(e[t]+e[t-1]+... +e[1])
最后，再根据M，对c[t]进行限幅即可
首先要计算切换函数，理论上来说，切换函数可以使用:
s[t]= a*e[t]+b*e[t-1]
当s[t]>0时，c[t]=M 当s[t]<0时，c[t]=-M
符号说明：
r[t]:当前系统设定值（给定量）
c[t]:系统输出值（控制量）
e[t]:当前系统设定值与系统输出值的差
e[t-1]:上一个控制周期系统的设定值与系统输出值的差值
Kp:常数，比例系数
Ki:常数，积分系数（积分时间）
Kd:常数，微分系数（微分时间）
s[t]：当前开关函数的计算结果
M:常数,由于智能车一般不会满电压（占空比）跑，M是一个限幅值，输出的电压（或占空比）应该被限制在[-M,M]的范围内。
三、模糊控制
扎德(L.A.Zadeh)教授在1965年提出模糊逻辑，并于1973年提出把模糊逻辑应用于控制理论。模糊控制属于早期智能控制的一种。
模糊控制器（也叫做“模糊逻辑控制器”）的基本结构：
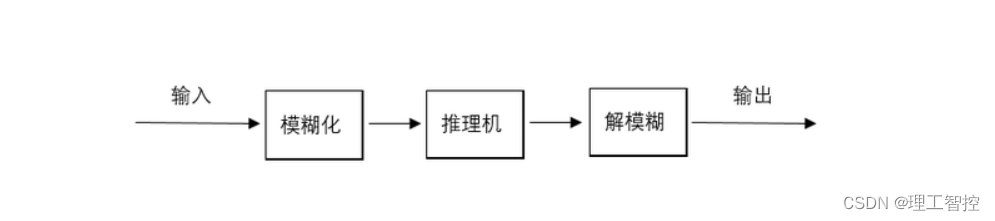
什么是“模糊”？：
我们以电机转速为例，简单理解一下“模糊”的概念：
对于电机的转速度r，我们可以使用r=3600转，r=4800转，这类精确的数值来进行描述。
此外还可以使用“转得快”，“转得慢”，没有转”，“转得非常快“等模糊语言进行描述。
比如，当我们定义4000转为“转得快”，2000，转为“转得慢”，那么，对于r=3800转，时，有a4000+b2000 = 3800( b=a-1)解方程得a=0.9 , b=0.1
我们可以认为，r=3800转九成属于“转得快”，一成属于“转得慢”。
这个过程就是“模糊化”。其中a=0.9称为r关于“转得快”的隶属度，b=0.1称为r关于“转得慢”的隶属度。
模糊化
对于一个变量x，我们可以将其划分为七个等级：
| NB | 负 | 大 |
| NM | 负 | 中等 |
| NS | 负 | 小 |
| ZO | 零 | |
| PS | 正 | 小 |
| PM | 正 | 中等 |
| PB | 正 | 大 |
分别计算x关于NB,NM,NS,ZO,SP,PM,PB的隶属度，得到x的模糊集
X = (a(x),b(x),c(x),d(x),e(x),f(x),g(x))
其中，a(x),b(x),c(x),d(x),e(x),f(x),g(x)分别为NB,NM,NS,ZO,PS,PM,PB的隶属度函数:
一般情况下，隶属度函数满足
a(x)+b(x)+c(x)+d(x)+e(x)+g(x)=1
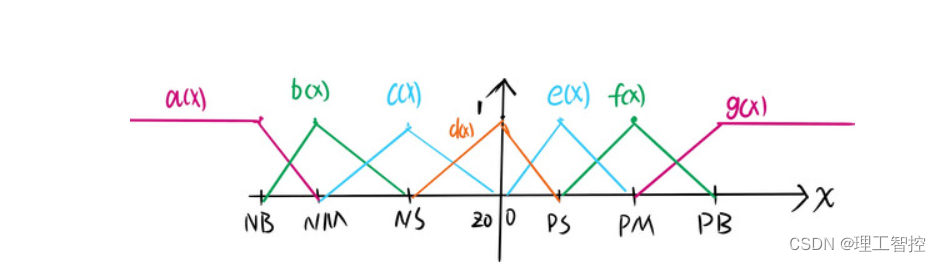
2．模糊规则表
模糊规则表中包含了人类关于某种控制过程的知识和经验，它是模糊控制的重要组成部分。
而推理机的作用是：将输入变量对应的模糊集通过查表的方式，转换为输出变量的模糊集。
比如一个输入变量的模糊集：
x = (0.1, 0.8, 0.1, 0, 0, 0)
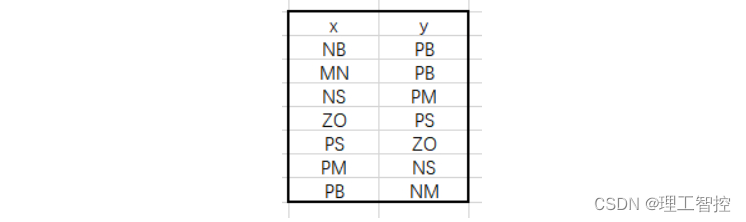
通过查表得到输出变量的模糊集：
y = (0, 0, 0, 0, 0.1, 0.9)
(其中0.9 = 0.8+0.1)。
解模糊
解模糊是模糊化的逆过程:
对于输出变量y,我们也将其划分为七个等级：
NB ,NM,NS,ZO,PS,PM,PB
这些等级分别对应的数值为
y1,y2,y3,y4,y5,y6,y7
从而，对于已知的模糊集
y = (s1,s2,s3,s4,s5,s6,s7)
我们可以计算出y的精确数值：
y = s1*y1+ s2*y2+s3*y3+s4*y4+ s5*y5+ s6*y6+s7*y7
四、自适应控制
前面介绍的几种控制方法，都需要具体的参数，比如PID控制中的kp,ki,kd。只有这些参数调整为合适的数值，才能使控制器工作在最佳状态。而自适应控制器可以自动计算出参数，一方面，减少了调节参数的麻烦；另一方面，一定程度上可以根据环境的变化，灵活地对控制器做出调整。
自适应过程是一个不断逼近目标的过程。它所遵循的途径以数学模型表示，称为自适应算法。通常采用基于梯度的算法，其中最小均方误差算法（即LMS算法）尤为常用。自适应算法可以用硬件(处理电路)或软件（程序控制）两种办法实现。前者依据算法的数学模型设计电路，后者则将算法的数学模型编制成程序并用计算机实现。
自适应控制器的种类和结构有很多种。
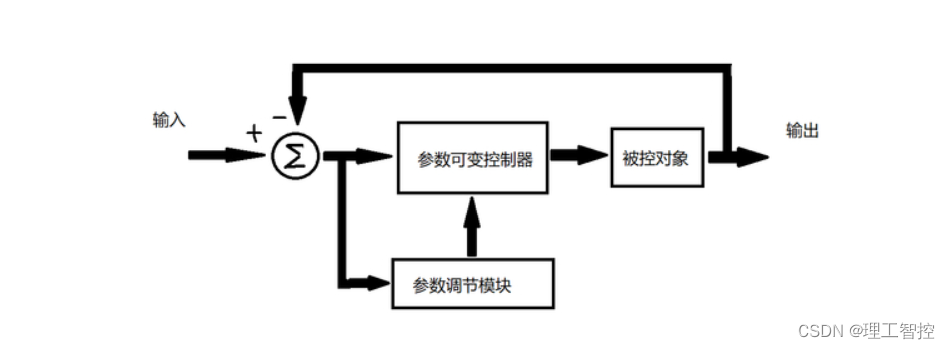
五、小结
运动控制算法多种多样，但是最常用的还是PID算法，实际在使用过程中还是需要根据需求和场景去选择算法。
最后
以上就是活泼书本最近收集整理的关于浅谈机器人基础概论--运动控制算法一、PID控制二、滑模变结构控制三、模糊控制四、自适应控制五、小结的全部内容，更多相关浅谈机器人基础概论--运动控制算法一、PID控制二、滑模变结构控制三、模糊控制四、自适应控制五、小结内容请搜索靠谱客的其他文章。
![[运动控制算法]模型预测控制前言一、基于运动学模型的模型预测控制二、项目演示三、总结四、参考](/uploads/reation/bcimg1.png)
发表评论 取消回复