本科期间做的一个课程设计，觉得比较好玩，现将之记录下来，实验所用图库及源程序。

1、实验目的

（1）学习主成分分析（PCA）的基础知识；
（2）了解PCA在人脸识别与重建方面的应用；
（3）认识数据降维操作在数据处理中的重要作用；
（4）学习使用MATLAB软件实现PCA算法，进行人脸识别，加深其在数字图像处理中解决该类问题的应用流程。

2、实验简介（背景及理论分析）

• 近年来，由于恐怖分子的破坏活动发生越发频繁，包括人脸识别在内的生物特征识别再度成为人们关注的热点，各国均纷纷增加了对该领域研究的投入。同其他生物特征识别技术，如指纹识别、语音识别、虹膜识别、DNA识别等相比，人脸识别具有被动、友好、方便的特点。该技术在公众场合监控、门禁系统、基于目击线索的人脸重构、嫌疑犯照片的识别匹配等领域均有广泛应用。
• 人脸识别技术是基于人的脸部特征，对输入的人脸图像或者视频流，首先判断其是否存在人脸。如果存在人脸，则进一步的给出每个脸的位置、大小和各个主要面部器官的位置信息。其次并依据这些信息，进一步提取每个人脸中所蕴涵的身份特征，并将其与已知的人脸进行对比，从而识别每个人脸的身份。广义的人脸识别实际包括构建人脸识别系统的一系列相关技术，包括人脸图像采集、人脸定位、人脸识别预处理、身份确认以及身份查找等；而狭义的人脸识别特指通过人脸进行身份确认或者身份查找的技术或系统。
• 我们在处理有关数字图像处理方面的问题时，比如经常用到的图像查询问题：在一个几万或者几百万甚至更大的数据库中查询一幅相近的图像。其中主成分分析（PCA）是一种用于数据降维的方法，其目标是将高维数据投影到较低维空间。PCA形成了K-L变换的基础，主要用于数据的紧凑表示。在数据挖掘的应用中，它主要应用于简化大维数的数据集合，减少特征空间维数，可以用较小的存储代价和计算复杂度获得较高的准确性。PCA法降维分类原理如下图所示：
  
  如上图所示，其中五角星表示一类集合，小圆圈表示另一类集合。假设这两个类别可以用特征X和特征Y进行描述，由图可知，在X轴和Y轴上这两个类别的投影是重叠的，表明这些点的两个特征X和Y没有表现出突出的识别性；但两类的投影在Z轴上区分度较大，显示出很好的识别性。

3、问题描述

• 对于一幅图像可以看作一个由像素值组成的矩阵，也可以将之扩展开，看作一个矢量。如一幅N*N像素的图像可以视为长度为N的2次方的矢量，这样就认为这幅图像是位于N^2维空间中的一个点，这种图像的矢量表示就是原始的图像空间，但是这个空间仅是可以表示或者检测图像的许多个空间中的一个。无论子空间的具体形式如何，这种方法用于图像识别的基本思想都是一样的，首先选择一个合适的子空间，图像将被投影到这个子空间上，然后利用对图像的这种投影间的某种度量来确定图像间的相似度，最常见的就是各种距离度量。
  通常需要处理的原始数据有以下特性：
  （1）数据的不同维数之间线性相关；
  （2）数据中的信息量分布不均匀，即有些方向数据分布集中，有些方向信息量较少；
  （3）一些较少的信息量去掉以后，对原始数据的分析并不产生太大的影响。
• 我们可考虑去掉那些包含信息量较少的数据，只保留包含信息量大的数据，这样就可以减少计算量，抓住问题的主要矛盾，忽略次要矛盾。在本实验中，我们采用了ORL人脸数据库：由40人、每人10幅、共400幅图像组成，每幅图像的分辨率为92×112，灰度级为256。这些图像是在不同时间、不同光照、面部表情和面部遮掩物不同的情况下获得的，如笑或不笑、眼睛或睁或闭、戴不戴眼镜。人脸姿态也有相当程度的变化，深度旋转和平面旋转可达20°，人脸尺度也有多达10％的变化。我们在此基础上，研究如何通过PCA人脸识别技术将一张图片重建，重建原理是什么以及如何将之较好地实现。

4、实现方法

（1）读取训练集图像信息

• 一张人脸图片在计算机表示为一个像素矩阵，即是一个二维数组，先把其变成一维数组，即把第一行后面的数全部添加到第一行。之后读取测试集目录下指定个数的图像，然后将其保存在一个二维数组中。如果图像个数为m，图像长宽为i、j，则我们创建一个二维数组A[m][i*j=n]用来保存图像数据。该数组中每一行表示一个图像的所有像素信息，每一列表示不同图像同一位置的像素信息。

（2）每列减去均值

• 将步骤1的每列减去该列的均值，这样每列的数据均值为0，对每一列求均值后也能得到平均脸。在利用matlab自带的函数princomp执行PCA的过程中，其会首先将每一列减去该列均值，不用另行计算。

（3）计算协方差矩阵

• 标准差和方差是用来描述一维数据，但现实生活我们常常遇到含有多维数据的数据集。当需要了解不同维度之间的关系时，我们就要用协方差。协方差就是一种用来度量两个随机变量关系的统计量。其定义为：
  
• 即协方差矩阵是一个对称的矩阵，对角线是各个维度上的方差。如果两个随机变量的协方差为正或为负，表明两个变量之间具有相关性，且协方差绝对值越大，两者对彼此的影响越大；如果为零，说明两个变量互相独立。因而通过计算协方差矩阵，我们就可以获得不同像素之间的关系。

（4）计算协方差矩阵的特征值与特征向量

• 由于协方差矩阵是实对称阵，可以计算其所有的特征值和特征向量。一般情况下构建出的协方差矩阵都会很大，直接计算起来会很复杂，所以一般都通过奇异值分解（SVD）求解该协方差矩阵的特征值以及特征向量，其基本理论过程为：
  
  

（5）选择主成分

• 通常随机变量方差越大，其包含的信息越多。协方差矩阵中对应的特征值大小决定了特征向量的重要性，故可选择那些包含最多信息的特征向量组成子集——特征向量矩阵（即为特征脸空间）。
• 首先需要将特征值按降序排列，我们可先绘制特征值的方差贡献率图像，之后根据精度要求选出我们感兴趣的前k个特征值所对应的特征向量（通常所选择的特征向量数k远小于n）。对应较大特征值的特征向量也称主分量，用于表示人脸的大体形状，如人脸框架，光照等等；而对应于较小特征值的特征向量则用于描述人脸的具体细节；从频域来看，主成分表示了人脸的低频部分，较小的分量则描述了人脸的高频部分。

（6）将训练集进行降维

• 此步骤是主要将原始的训练集进行降维变换，原始的图像数据是m* n的矩阵，只包含主成分的特征向量构成一个n* k的矩阵（每一列都是一个特征向量）。将两个矩阵相乘后，即把原始样本点分别往特征向量对应的轴上做投影，即可获得降维之后的图像矩阵m*k，降维后特征子空间中的任意一点对应于一幅图像。任何一幅人脸图像都可以向其投影并获得一组坐标系数，这组系数便可作为人脸识别的依据，也就是这张人脸图像的特征脸特征，即说明任何一幅人脸图像都可以表示为这组特征脸的线性组合。

（7）将测试集进行降维

• 同步骤6相似，读取所有的测试集图像，然后对其进行类似降维操作过程。如果测试集有h幅图像，则降维后的矩阵为h*k。

（8）人脸识别

• 该步骤为人脸识别的最后一步，用来对测试集进行识别，并计算识别准确率。人脸识别是先给出一张待识别的图像，在已经训练好的人脸特征空间中，计算待识别图像与已有的人脸之间的距离。当这个距离小于一定程度时，就认为该图像是一张人脸图像，否则就不是人脸图像。其终端输出的是训练构成的人脸空间与测试构成的人脸空间的欧式距离，相关图像之间欧式距离最小时，即最符合相应图像类型，给出与之最近的图像。与原始的图像匹配过程相比，本实验由于对图像进行了降维，在我们的实验中图像匹配速度提升了200倍以上。

5、实验结果（调试及优化）

（1）原理实现结果：

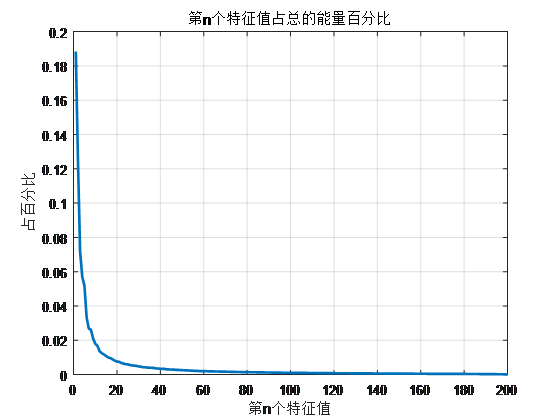
分析：

• 排列在前面的特征值占总的能量百分比高，排列在后面的占总能量百分比低，由曲线的斜率开始十分陡峭，后来十分平缓，以及曲线下对应的面积，可以看出能量主要集中在前一部分特征值。
  
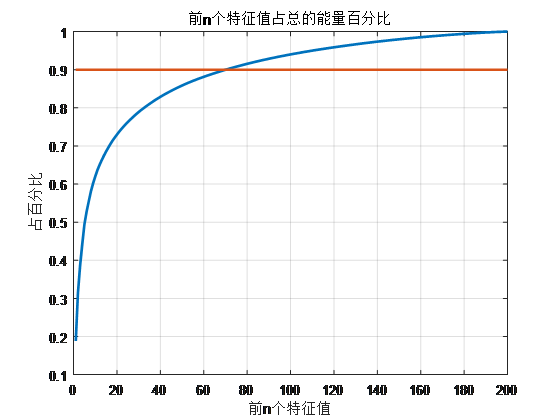
  分析：
• 设定90%的能量线，从上图可以看出，前60到80个特征值的能量累积就可以达到。且由此说明表达一幅图像的主要信息只需要前几十个特征值而并非全部，这是PCA技术的体现。
  
  分析：
• 第1分量表达了人脸的大致轮廓，是低频成分，对应的特征值大；随着分量数的增加，图像显示出更多细节，是高频成分，对应特征值逐渐减小。

（2）图像重建结果：

分析：

• 由上图可知，就其横向而言，参数取值越大，重建图像越清晰；就纵向而言，测试集与训练集重建效果无明显差别，非人脸图像作为对照无法重建出人脸。
  
  分析：
• 第一幅训练集图像，第二幅测试集图像，第三幅非人脸图像。经过对三组图像进行对比可得出：训练集、测试集图像重建效果较为模糊，但在可识别范围内（重建图像参数取值199）；非人脸图像会依照其自身特点重建出一幅极为模糊的图像。

（3）对照实验结果：

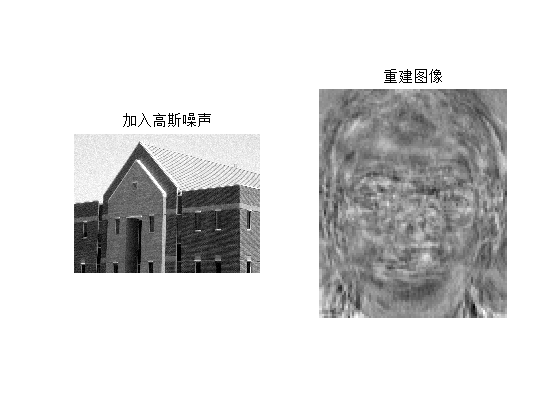
分析：

• 由上面图像可知，若原图像中含有高斯噪声时，三组图片都无法识别出人脸，说明高斯噪声对重建效果影响很大，因而在识别前对图像进行一定去噪处理极为必要。
  
  
  
  分析：
• 由上面结果可知，滤除高斯噪声后进行重建的效果与原始图像重建效果相比，无明显差别；但与上面含有噪声的图像重建效果相比，有很大的改良作用。
  
  
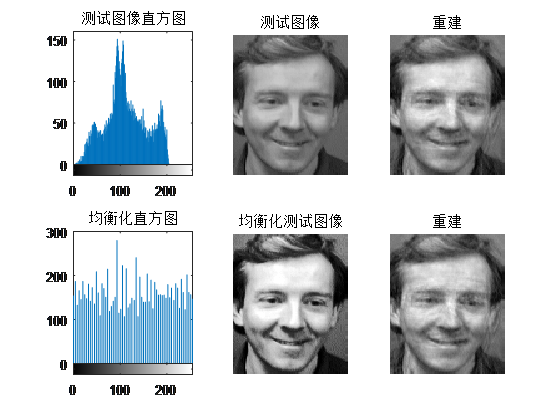
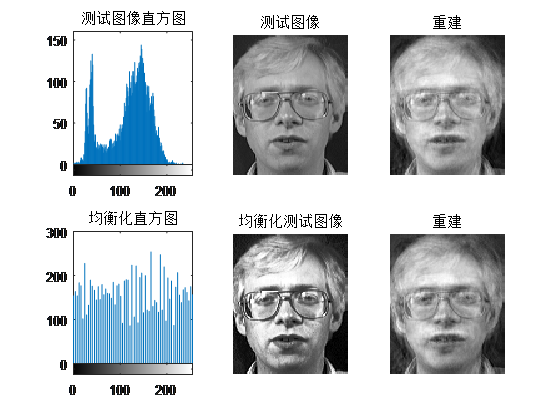
  分析：
• 直方图均衡化后增强了图像对比度，无论是测试图像还是重建后的图像，整体变亮。

（4）识别正确率：

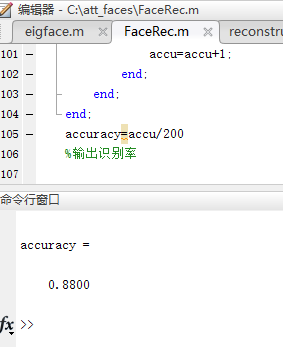
分析：

• 由上图所示，这是200张测试图像的识别正确率。经过多次调试知，对于400张图像，当训练库图像与测试库图像各位200张时识别正确率最大，为88％。这就说明了并不是所有的特征向量都有效代表了人脸信息，有的特征向量代表的可能是与人脸信息无关的噪声、背景等无效信息，把这些特征向量加入会导致识别率的下降。

6、实验结论

• 本文主要是基于PCA算法实现了人脸识别程序，使用的数据库是ORL人脸数据库，采用最小欧氏距离来分类，最终能对测试图像进行较为精准地识别，得到较好的实验结果。但本实验中仍存在一些问题，所使用的数据比较少，且人脸图像比较好，没有光照的影响，这些都是需要考虑的。因而后人又在其基础上提出了Mat PCA算法、2DPCA算法、Module PCA算法等一系列改进算法。这些算法在人脸识别速度或识别率等方面有一定的提升，将一些人脸识别算法组合是今后研究的一种趋势，由于时间有限，此处不做过多介绍。

7、附 注

【1】最大方差理论：是指在信号处理中可以认为信号具有较大的方差，噪声有较小的方差，信噪比就是信号与噪声的方差比，故越大越好。
【2】欧氏距离：是一个通常采用的距离定义，指在m维空间中两个点之间的真实距离，或者向量的自然长度（即该点到原点的距离），在二维和三维空间中的欧氏距离的就是两点之间的实际距离。
【3】维度灾难：在数字图像处理中，对于已知样本数目，存在一个特征数目的最大值，当实际使用的特征数目超过这个最大值时，分类器的性能就会退化，这与训练集样本数目直接相关。

最后

以上就是阔达鲜花为你收集整理的基于主成分分析（PCA）的人脸识别技术1、实验目的2、实验简介（背景及理论分析）3、问题描述4、实现方法5、实验结果（调试及优化）6、实验结论7、附 注的全部内容，希望文章能够帮你解决基于主成分分析（PCA）的人脸识别技术1、实验目的2、实验简介（背景及理论分析）3、问题描述4、实现方法5、实验结果（调试及优化）6、实验结论7、附 注所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。