数字信号处理翻转课堂笔记5

The Flipped Classroom5 of DSP

对应教材：《数字信号处理（第五版）》西安电子科技大学出版社，高西全，丁玉美著

一、要点

1、回顾序列z变换概念：定义、收敛域、性质；
2、求逆z变换的方法：留数法，部分分式展开法；
3、回顾利用z变换求解离散LTI系统；
4、离散LTI系统频率响应的概念；
5、系统函数零极点分布对系统频率响应的影响（重点和难点）；
6、离散全通系统、离散最小相位系统、梳状滤波器的概念。
通过这节课的学习，应该能深入理解离散LTI系统的系统函数零极点与系统频率响应特性之间的关系，掌握数字系统频率响应所具有的周期性、对称性等特点。

二、问题与解答

1、总结不同类型（有限长、右边、左边、双边）序列收敛域的特点。什么情况下，z变换不存在？
2、根据实序列傅里叶变换的特点，讨论单位响应h(n)为实序列的离散LTI系统的频率响应具有什么特点（奇偶对称性、周期性等等）？据此进一步讨论离散LTI系统频率响应的频率轴有效范围以及数字低频、数字高频在频率轴的位置，与连续系统的频率响应相比有什么区别？
3、基于上一题的结果，分别画出理想低通、高通、带通数字滤波器在ω=（-4π，4π）区间的幅频响应波形（手绘）。
4、基于z平面的零点向量和极点向量，详细分析系统函数零极点位置对离散LTI系统频率响应的影响。在此基础上，进一步讨论全通系统、最小相位系统、梳状滤波器零极点分布的特点与其各自特性之间的联系。
5、通过在z平面适当位置设置相应的零点和极点，设计一个具有某种滤波特性（如梳状滤波器、带通滤波器、带阻滤波器）的系统（确定系统函数H(z)）。利用MATLAB软件，绘制该系统的幅频响应和零极点图（利用zplane和freqz函数，参见教材上相关例子），讨论其幅频响应曲线和零极点位置之间的关系。
6、根据上一步设计的滤波器的滤波特性，选用一个由多个频率的余弦序列组成的信号（应该有些频率位于所设计滤波器的阻带，有些频率位于滤波器的通带），利用MATLAB，求该序列通过滤波器之后的稳态输出，画出输出信号的幅度谱（用filter函数求零状态响应，取其中的稳态部分画频谱），并与输入序列的幅度谱进行比较，据此分析滤波器所起的滤波作用。

1、z变换收敛域问题

总结不同类型（有限长、右边、左边、双边）序列收敛域的特点。什么情况下，z变换不存在？

2、离散LTI系统的频率响应特点

根据实序列傅里叶变换的特点，讨论单位响应h(n)为实序列的离散LTI系统的频率响应具有什么特点（奇偶对称性、周期性等等）？据此进一步讨论离散LTI系统频率响应的频率轴有效范围以及数字低频、数字高频在频率轴的位置，与连续系统的频率响应相比有什么区别？

单位响应h(n)为实序列的离散LTI系统的频率响应就是其傅里叶变换，具有共轭对称性质，幅度是w的偶函数，相位是w的奇函数；具有周期性，周期是2π。
离散LTI系统频率响应的频率轴有效范围一般取一个周期，加上幅度是w的偶函数，因此w的的频率轴有效范围是[0,π]。数字低频：w=2πn（n取整数）；数字高频：w=（2n+1）π（n取整数）。所以在[0,π]范围中，数字低频是w=0 , 数字高频是 w=π。

3、低通、高通、带通数字滤波器的幅频响应

基于上一题的结果，分别画出理想低通、高通、带通数字滤波器在ω=（-4π，4π）区间的幅频响应波形（手绘）。

4、零极点位置对频率响应的影响及全通/最小相位/梳状滤波器的零极点分布

基于z平面的零点向量和极点向量，详细分析系统函数零极点位置对离散LTI系统频率响应的影响。在此基础上，进一步讨论全通系统、最小相位系统、梳状滤波器零极点分布的特点与其各自特性之间的联系。

系统函数零极点位置对离散LTI系统频率响应的影响：
（1）极点位置主要影响频响的峰值位置及其尖锐程度。
（2）零点的位置影响频响的谷点位置及其形状。
详细分析：
由零点C（用圆圈表示）指向单位圆上B的向量为零点向量，由极点C’’（用叉号表示）指向单位圆上B（B为单位圆上的任意一点）的向量为极点向量。

当B点转到极点附近时，极点向量长度最短，因而幅度特性可能出现峰值，并且极点越接近单位圆，峰值愈高愈尖锐。
则得到结论为极点位置主要影响频响的峰值位置及其尖锐程度。

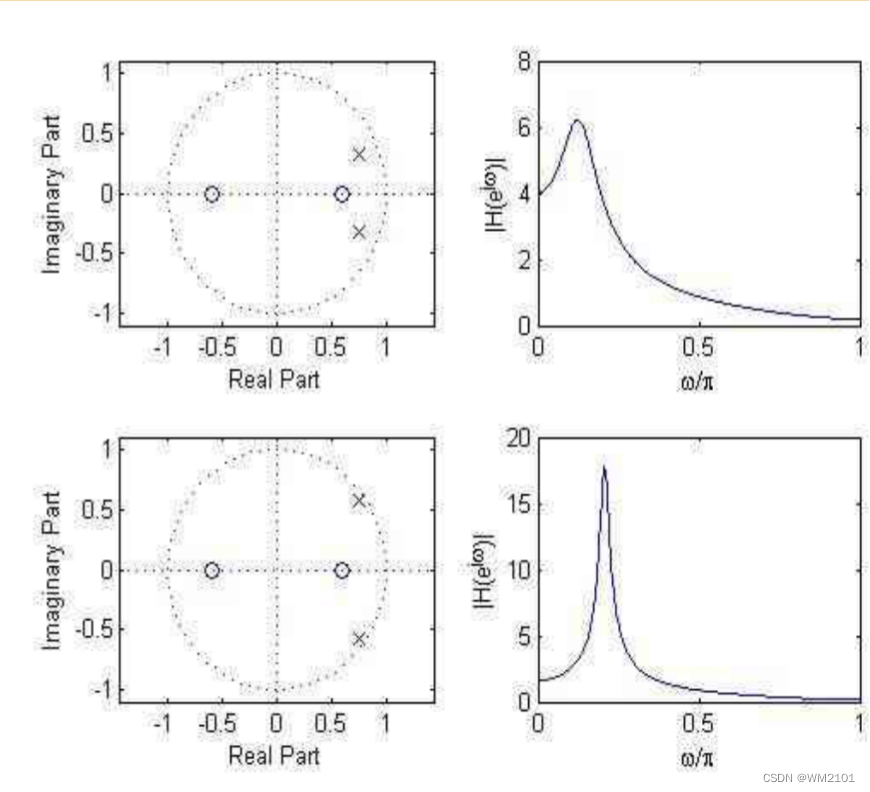
当B转到零点附近时，幅度特性将出现谷值，零点越靠近单位圆，谷值越小，当在单位圆上时，谷值为0。
则得到结论为：零点的位置影响频响的谷点位置及其形状。

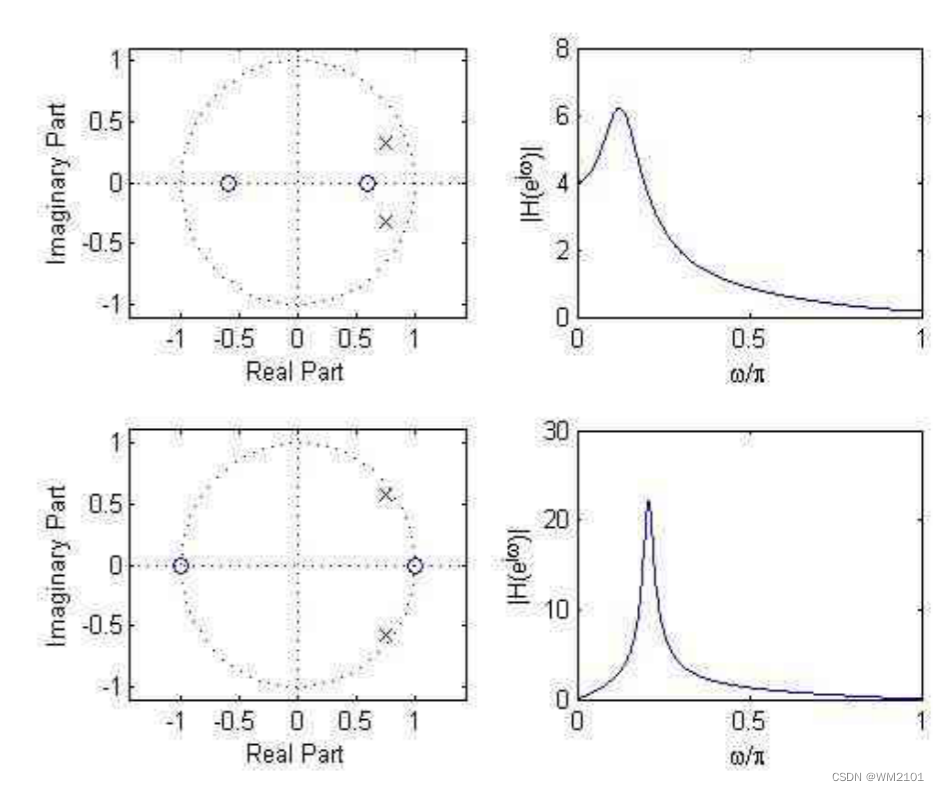
全通系统定义：滤波器的幅频特性对所有频率均等于常数或1，不一定为1，即：| H（e^jw ）| = 1 (0≤ω≤2π) 信号通过全通滤波器之后，幅度谱保持不变，仅相位谱随φ（ω）改变，起纯相滤波作用。全通滤波器的极点零点分布特点：
1、零极点互为倒数关系，零极点是镜像对称的，若z=re^jθ是零点，则对应的极点是z=1/r e^(-jθ)。
2、所有的零极点对在Z平面上都是复共轭的。
3、当N=1时，零点、极点均为实数。

最小相位系统：一个因果稳定系统的所有极点必在单位圆内，如果因果稳定系统的零点也在单位圆内，则称之为最小相位系统。即所有的零点都在单位圆内的传输函数为最小相位系统。
最小相位系统系统函数H(z)零极点分布特点：
1、所有的极点在单位圆内，所有的零点在单位圆内,可以在单位圆上。非最小相位系统由一个最小相位系统和全通系统级联而成。记为Hmin(z);
2、所有零点都在单位圆外，则称之为“最大相位系统”，记为Hmax(z)；
3、单位圆内、外都有零点，则称之为“混合相位系统”。
4、非最小相位系统外的零点可以用1/zok*来镜像代替，构建成为最小相位系统，且幅频响应特性相同。
5、任何一个最小相位系统的相位延迟最小。

梳状滤波器：梳状滤波器它是由许多按一定频率间隔相同排列的通带和阻带，只让某些特定频率范围的信号通过。在频域上按照均匀间隔零极点交替出现，呈“梳齿状”频响。梳状滤波器可以滤除ω=2π/N k的频率分量，H(Z^N )=(1-Z^(-N))/(1-aZ(-N) )，a取值越趋近于1，幅频特性越平坦。
零极点分布特点：零点在单位圆上，极点在半径为a^(1/N)的圆上.
关系：
1、任何一个非最小相位系统的系统函数H(z)均可由一个最小相位系统Hmin(z)和一个全通系统Hap(z)级联而成。非最 小相位系统外的零点可以用1/z0k*来镜像代替，构建成为最小相位系统，且幅频响应特性相同
2、在幅频响应特性相同的所有因果稳定系统集中，最小相位系统的相位延迟（负的相位值）最小。任何一个非最小相位系统H(z)的相位函数，是一个与H(z)的幅频特性相同的最小相位系统Hmin(z)的相位函数加上一个全通系统Hap(z)的相位函数。全通系统Hap(z)的相位函数是非正的。
最小相位系统保证其逆系统存在。

5、利用零极点知识，设计一个滤波器

通过在z平面适当位置设置相应的零点和极点，设计一个具有某种滤波特性（如梳状滤波器、带通滤波器、带阻滤波器）的系统（确定系统函数H(z)）。利用MATLAB软件，绘制该系统的幅频响应和零极点图（利用zplane和freqz函数，参见教材上相关例子），讨论其幅频响应曲线和零极点位置之间的关系。
代码：
设计一个梳状滤波器，可以滤除数字频率在0、0.5π和π的频率分量

%设计一个梳状滤波器，可以滤除数字频率在0、0.5π和π的频率分量
%%      代码：
B=[1 0 0 0 -1];
A=1;
subplot(3,1,1);
zplane(B,A);                %zplane:离散时间系统的零极点图
[H,w]=freqz(B,A);           %freqz:数字滤波器的频率响应
subplot(3,1,2);
plot(w/pi,abs(H));
axis([0,1,0,2.5]);
subplot(3,1,3);
plot(w/pi,angle(H)); 

运行结果：

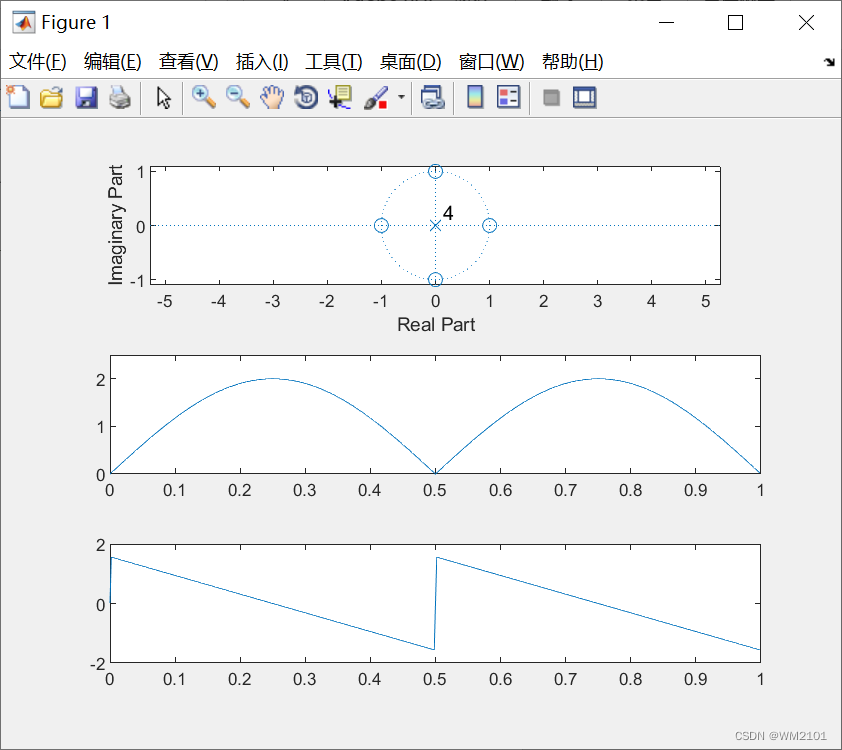
分析：
第一幅图中，由于零点在0,0.5π，π，1.5π处，所以此处都应是“谷值”，在第二幅图中可以体现。

6、探究验证滤波器的功能

根据上一步设计的滤波器的滤波特性，选用一个由多个频率的余弦序列组成的信号（应该有些频率位于所设计滤波器的阻带，有些频率位于滤波器的通带），利用MATLAB，求该序列通过滤波器之后的稳态输出，画出输出信号的幅度谱（用filter函数求零状态响应，取其中的稳态部分画频谱），并与输入序列的幅度谱进行比较，据此分析滤波器所起的滤波作用。
代码：

%%      代码：
%设计一个梳状滤波器，可以滤除数字频率在0、0.5π和π的频率分量
figure(1)
B=[1 0 0 0 -1];
A=1;
subplot(3,1,1);
zplane(B,A);                            %zplane函数:离散时间系统的零极点图
[H,w]=freqz(B,A);                       %freqz函数:数字滤波器的频率响应
subplot(3,1,2);plot(w/pi,abs(H));
axis([0,1,0,2.5]);
subplot(3,1,3);plot(w/pi,angle(H));
 
figure(2)
X=dirac(w-0.5*pi)+dirac(w-0.25*pi);     %dirac函数：狄拉克函数（冲激函数）
X=pi*sign(X);                           %sign函数：符号函数
subplot(2,1,1)
plot(w/pi,abs(X));
XX=X.*H;                                %X通过H滤波器
subplot(2,1,2)
plot(w/pi,abs(XX));

运行结果：

如图可见，频率分量在0.5π处的冲激被梳状滤波器过滤掉了。

三、反思总结

1、matlab中的函数：
zplane函数：离散时间系统的零极点图
freqz函数：数字滤波器的频率响应
dirac函数：狄拉克函数（冲激函数）
sign函数：符号函数

最后

以上就是魁梧小伙为你收集整理的数字信号处理翻转课堂笔记5数字信号处理翻转课堂笔记5The Flipped Classroom5 of DSP的全部内容，希望文章能够帮你解决数字信号处理翻转课堂笔记5数字信号处理翻转课堂笔记5The Flipped Classroom5 of DSP所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。