数字信号处理matlab——系统响应和系统稳定

119 阅读 0 评论 79 点赞

我是靠谱客的博主心灵美美女，最近开发中收集的这篇文章主要介绍数字信号处理matlab——系统响应和系统稳定，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

时域中，描绘系统特性的方法是差分方程和单位脉冲响应。
频域中，描绘系统特征的方法可以是系统函数
系统线性时不变特性，因果性，稳定性
稳定性是对于任意有界的输入信号，系统能得到有界的响应。
系统的单位脉冲响应满足绝对可和
系统稳定性可以从差分方程系数得出
检查系统稳定性最普遍的做法是：输入单位阶跃序列，当n→∞，系统输出趋近于一个常数，那么系统是稳定的

例一

给定一个差分方程
y(n)=0.05x(n)+0.05x(n-1)+0.9y(n-1)
输入信号x(n)=R8(n)
求x(n)的系统响应，画出波形
求出单位脉冲响应

clc
close all;
clear all;
A=[1,-0.9];
B=[0.05,0.05];
xn=[ones(1,8),zeros(1,42)];
n=0:length(xn)-1;
[hn,n]=impz(B,A,length(xn));
yn=filter(B,A,xn);
figure
subplot(2,1,1);
xlabel('n');
ylabel('y(n)');
stem(n,yn,'.');
axis([0,length(n),min(yn),1.2*max(yn)]);
title('System response to R8(n)');

subplot(2,1,2);
xlabel('n');
ylabel('h(n)');
stem(n,hn,'.');
axis([0,length(n),min(hn),1.2*max(hn)]);
title('System unit impulse response');

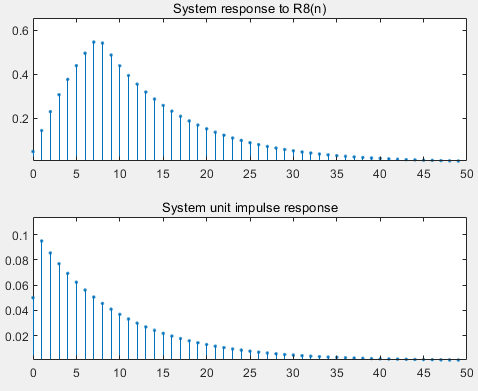
在这里插入图片描述

信号经过低通滤波器，信号的高频被过滤，时域信号的变化减缓，在有阶跃处附近产生过渡带。因此输入矩形序列时，输出序列的开始和终了都产生明显的过渡带。输入为单位阶跃时，中了也产生明显过渡带

例二

给定一个差分方程
y(n)=0.05x(n)+0.05x(n-1)+0.9y(n-1)
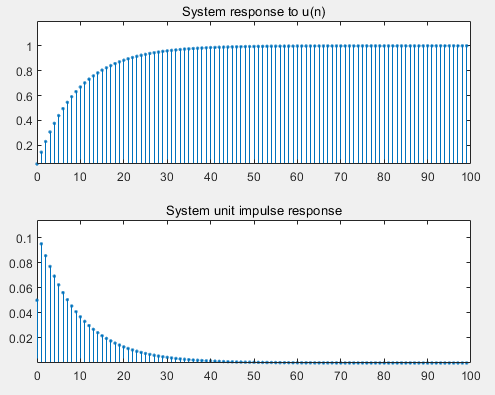
输入信号x(n)=u(n)
求x(n)的系统响应，画出波形
求出单位脉冲响应

clc
close all;
clear all;
A=[1,-0.9];
B=[0.05,0.05];
xn=ones(1,100);
n=0:length(xn)-1;
[hn,n]=impz(B,A,length(xn));
yn=filter(B,A,xn);
figure
subplot(2,1,1);
xlabel('n');
ylabel('y(n)');
stem(n,yn,'.');
axis([0,length(n),min(yn),1.2*max(yn)]);
title('System response to u(n)');

subplot(2,1,2);
xlabel('n');
ylabel('h(n)');
stem(n,hn,'.');
axis([0,length(n),min(hn),1.2*max(hn)]);
title('System unit impulse response');

在这里插入图片描述

例三

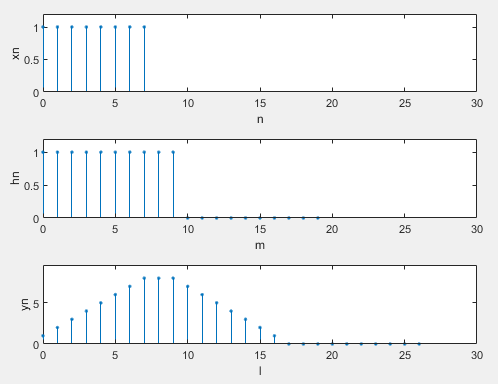
给定系统的单位脉冲响应h(n)=R10(n),
用线性卷积法求x(n)=R8(n)对系统h(n)的输出响应y(n)

clc
close all;
clear all;
xn=ones(1,8);
n=0:length(xn)-1;
figure
subplot(3,1,1);
stem(n,xn,'.');
xlabel('n');
ylabel('xn');
axis([0,30,0,1.2*max(xn)]);

hn=[ones(1,10),zeros(1,10)];
m=0:length(hn)-1;
subplot(3,1,2);
stem(m,hn,'.');
xlabel('m');
ylabel('hn');
axis([0,30,0,1.2*max(hn)]);

yn=conv(hn,xn)
l=0:length(xn)+length(hn)-2;
subplot(3,1,3);
stem(l,yn,'.');
xlabel('l');
ylabel('yn');
axis([0,30,0,1.2*max(yn)]);

在这里插入图片描述

例四

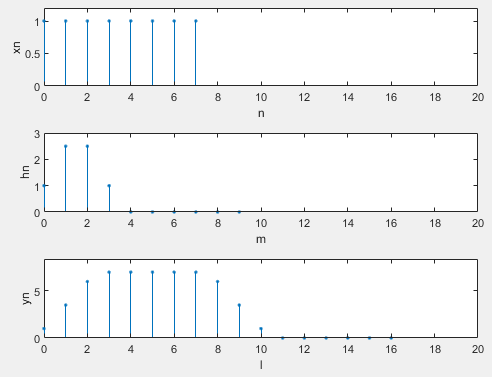
给定系统的单位脉冲响应h(n)=δ(n)+2.5δ(n-1)+2.5δ(n-2)+δ(n-3)
用线性卷积法求x(n)=R8(n)对系统h(n)的输出响应y(n)

clc
close all;
clear all;
xn=ones(1,8);
n=0:length(xn)-1;
figure
subplot(3,1,1);
stem(n,xn,'.');
xlabel('n');
ylabel('xn');
axis([0,20,0,1.2*max(xn)]);

hn=[1,2.5,2.5,1,zeros(1,6)];
m=0:length(hn)-1;
subplot(3,1,2);
stem(m,hn,'.');
xlabel('m');
ylabel('hn');
axis([0,20,0,1.2*max(hn)]);

yn=conv(hn,xn)
l=0:length(xn)+length(hn)-2;
subplot(3,1,3);
stem(l,yn,'.');
xlabel('l');
ylabel('yn');
axis([0,20,0,1.2*max(yn)]);

在这里插入图片描述

例五

y(n)=1.8237y(n-1)-0.9801y(n-2)+1/100.49x(n)-1/100.49x(n-2)

谐振器的谐振频率为0.4rad
输入信号为u(n)，输出为y(n)
求系统的稳定性和输出波形

clc
close all;
clear all;
un=ones(1,256);
n=0:length(un)-1;
A=[1,-1.8237,0.9801];
B=[1/100.49,0,-1/100.49];
yn=filter(B,A,un);
figure
stem(n,yn,'.');
xlabel('n');
ylabel('yn');
axis([0,length(un),1.2*min(yn),1.2*max(yn)]);

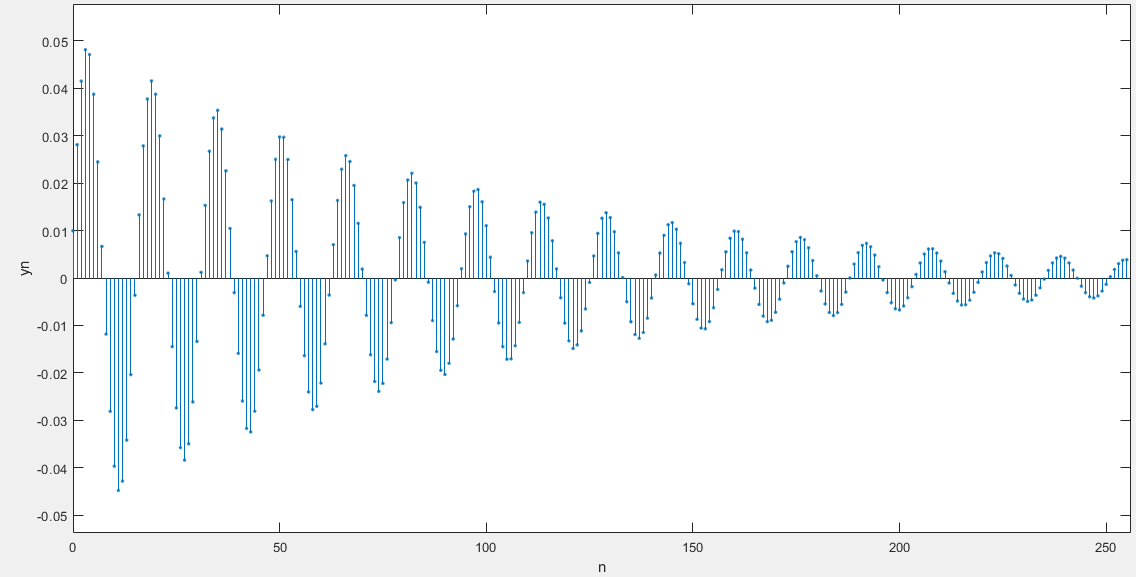
在这里插入图片描述
稳定
检验系统的稳定性
输入端加入单位阶跃序列，观察波形，波形稳定在一个常数值上，系统稳定，否则不稳定

例六

y(n)=1.8237y(n-1)-0.9801y(n-2)+1/100.49x(n)-1/100.49x(n-2)

谐振器的谐振频率为0.4rad
输入信号为x(n)=sin(0.014* n)+sin(0.4*n)，输出为y(n)
求系统输出波形

clc
close all;
clear all;
n=0:256;
xn=sin(0.014*n)+sin(0.4*n);
A=[1,-1.8237,0.9801];
B=[1/100.49,0,-1/100.49];
yn=filter(B,A,xn);
figure
stem(n,yn,'.');
xlabel('n');
ylabel('yn');
axis([0,length(n),1.2*min(yn),1.2*max(yn)]);

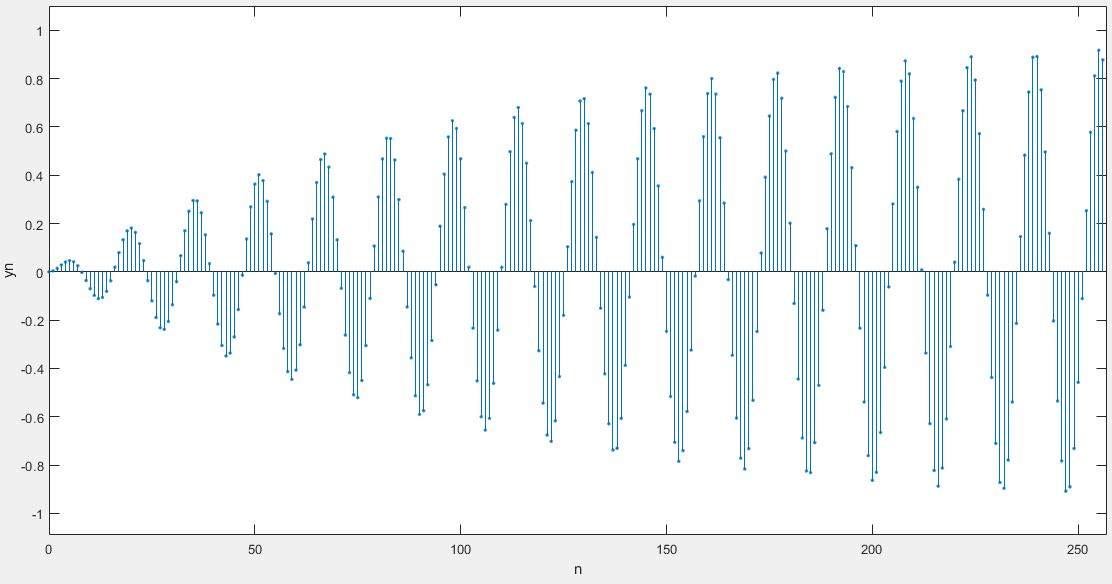
在这里插入图片描述
时域求系统响应方法有两种
1.通过差分方程求得系统输出，需要初始条件，是否是零输入响应
2.已知系统单位脉冲响应，通过求输入信号和系统单位脉冲响应的线性卷积求得系统输出