【MATLAB数字信号处理】离散时间系统的时域分析（一）

2.1 基础知识回顾

​ 对线性离散时间系统，若$y_1[n]$和$y_2[n]$分别是输入序列$x_1[n]$和$x_2[n]$的响应，则输入$x[n]=\alpha x_1[n]+\beta x_2[n]$的输出响应为$y[n]=\alpha y_1[n]+\beta y_2[n]$。上式的叠加性质对任意常量α和β以及任意输入$x_1[n]$和$x_2[n]$都成立。若存在一组非零的α和β值，或者一组非零的输入序列$x_1[n]$和$x_2[n]$，上式不成立，则为非线性系统。

​ 对于离散时不变系统，若$y_1[n]$是$x_1[n]$的响应，则输入$x[n]=x_1[n-n_0]$的输出响应为$y[n]=y_1[n-n_0]$，式中$n_0$是任意整数。上面的输入输出关系对任意输入序列及其响应的输出成立。若对至少一个输入序列及其相应的输出序列不成立，则为时变系统。

​ 若对于任意有界输入序列$x[n]$，其输出$y[n]$也是一个有界序列，则该离散时间系统是有界输入有界输出（BIBO）稳定的，即若$|x[n]|<B_x$(对所有n值)，则相应的输出$y[n]$也有界，即$|y[n]|<B_y$(对所有n值)，这里$B_x$和$B_y$都是有限常数。

​ 数字滤波器对单位样本序列$|y[n]|$的响应称为单位样本响应，简称为冲激响应，用$h[n]$表示。相应地，离散时间系统对单位阶跃序列$\mu [n]$的响应用$s[n]$表示，称为单位阶跃响应，简称为阶跃响应。

​ 输入信号$x[n]$的冲激响应$h[n]$可用来描述线性时不变离散系统的响应$y[n]$，表示为$y[n]={\sum }_{k=-\infty }^{\infty }h[k]x[n-k]$，通过简单的变量代换可表示成$y[n]={\sum }_{k=-\infty }^{\infty }h[n-k]x[k]$，上面两式中的和称为序列$x[n]$和$h[n]$的卷积和，表示为$y[n]=h[n]\ast x[n]$。

2.2 滑动平均滤波器

​ 滑动平均滤波器：$y[n]=\frac{1}{M}{\sum }_{k=0}^{M-1}x[n-k]$

% 用滑动平均滤波器去除噪声
R = 50;
d = rand(R,1)-0.5;
m = 0:1:R-1;
s = 2*m.*(0.9.^m);
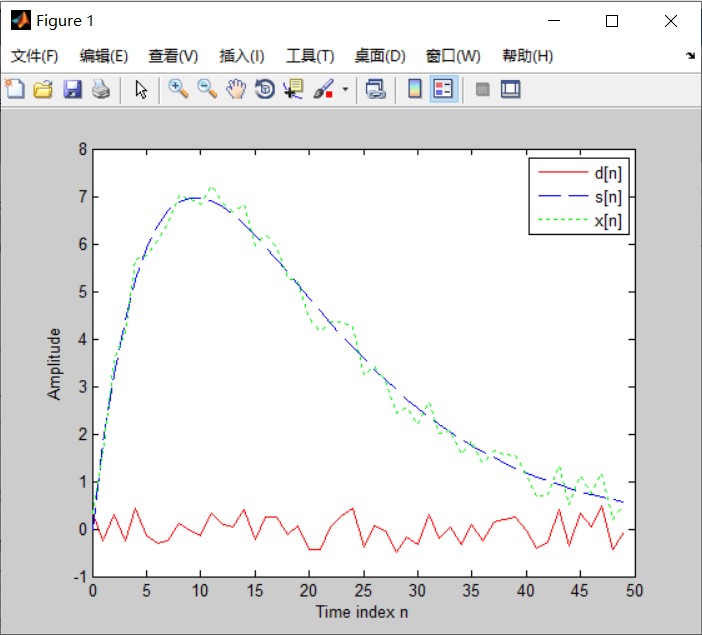
x = s + d';
plot(m,d,'r-',m,s,'b--',m,x,'g:')
xlabel('Time index n'); ylabel('Amplitude')
legend('d[n]','s[n]','x[n]');
pause
M = input('Number of input samples = ');
b = ones(M,1)/M;
y = filter(b,1,x);
plot(m,s,'r-',m,y,'b--')
legend('s[n]','y[n]');
xlabel ('Time index n');ylabel('Amplitude');

最后

以上就是彩色月饼为你收集整理的【MATLAB数字信号处理】离散时间系统的时域分析（一）的全部内容，希望文章能够帮你解决【MATLAB数字信号处理】离散时间系统的时域分析（一）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。