闭环系统的零极点图判定稳定性_12. Nyquist稳定性判据

第二种表示频率特性的图示方法是Nyquist Plot或者也叫Polar Plot，也就是把频率特性的实部与虚部在复平面上表示出来，角频率为变量。

从Nyquist Plot和Bode Plot出发，如果没有闭环传递函数的特征方程，如何从开环系统的传递函数或者频率响应得知闭环系统的稳定性呢？ 本篇文章就主要讨论Nyquist稳定性判据。

本篇目录

1. 临界稳定
2. Nyquist稳定性判据
3. 判断稳定性实例
4. 本篇小节

1. 临界稳定

我们以一个简单的闭环系统来说明。从根轨迹中我们看出：如果

，那么系统就是稳定的。反之

，系统则不稳定。

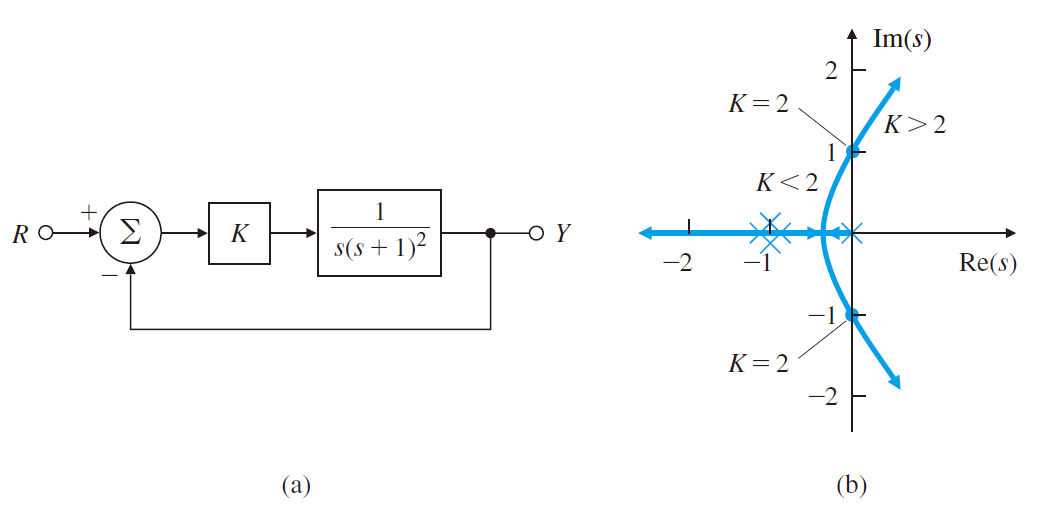
我们从闭环系统的根轨迹方程得知：

如果

并且是实数，那么我们有

于是每一个根轨迹上的点

都满足

和

。根轨迹在

时根轨迹落在虚轴之上，如之前稳定性的定义，该系统是临界稳定的。此时

，于是我们知道虚轴上的点满足

。

既然我们已经知道，频率特性中相角为-180度时的频率

对应的

在

时满足

。显然

时，此

的幅值满足

，当

时，幅值则

。在Bode Plot上我们可以很容易从相角为-180度的

是否大于1来判断该系统的稳定性。下图中左边为幅值，右边为dB。如果是dB，则看

是否大小0dB。

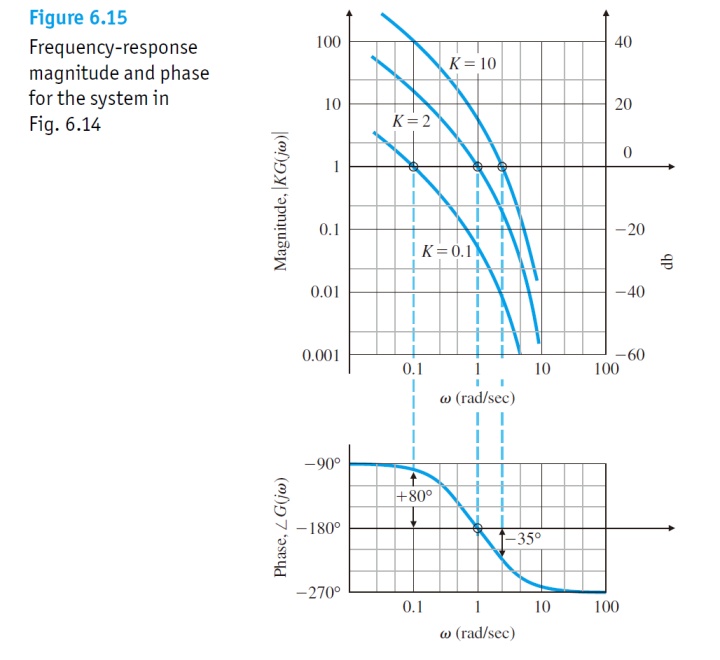
试想任何满足K增大从而导致不稳定的系统都会满足上述稳定性条件。然而，事情并没有那么简单。有些系统却是小增益不稳定，大增益稳定的。 此时上满的稳定性就不再成立了，并且恰好相反。更有系统的幅频曲线会穿越1或者0dB数次，从而这样的从Bode Plot去判断稳定性就变得不确定了。但是不管怎样，我们总是可以画根轨迹去判断KG的稳定性的。 由于Bode Plot对某些系统的稳定性判断并不是那么明朗，我们求助于Nyquist Plot并且介绍Nyquist稳定性判据。

2.Nyquist稳定性判据

大多数的系统在增益K增加时都会最终导致不稳定。这种关系在早期研究反馈时被认为几乎是一个普遍规律。然而反馈放大器的设计者们在实验室中发现放大器在增益减小时会趋向于不稳定。这让人费解的现象于是促成了1932年Bell实验室的Harry Nyquist的研究。研究结果称为了著名的Nyquist Stability Criterion。此时根轨迹方法的发明者Walter Richard Evans只有12岁，距离1948年发表根轨迹方法还有16年之久。

首先明确这个判据的理论基础：幅角原理（Argument principle），具体可以参见[1][2]。简单来说，在复平面中变量s走过一个右半平面的封闭曲线，若封闭曲线里包含了某个传递函数KG(s)的一个极点，则对应KG(s)按照s的取值在复平面中会逆时针绕过原点一次；若包含其零点，则会顺时针绕过一次。最终顺时针绕过原点的净圈数就是包围的零点数与极点数之差。

既然如此，我们把闭环特征方程写成这个传递函数F(s)，其零点就是闭环极点，极点是开环极点。

为了查看右半平面闭环极点的情况，等价于当s绕着整个右半平面顺时针一圈时，检查F(s)的曲线绕过原点的净圈数，也等同于检查KG(s)的曲线绕过(-1,0j)的净圈数。因为他们之间差了一个常数1。所以我们下面就可以全部转化为对KG(s)幅相曲线的讨论。

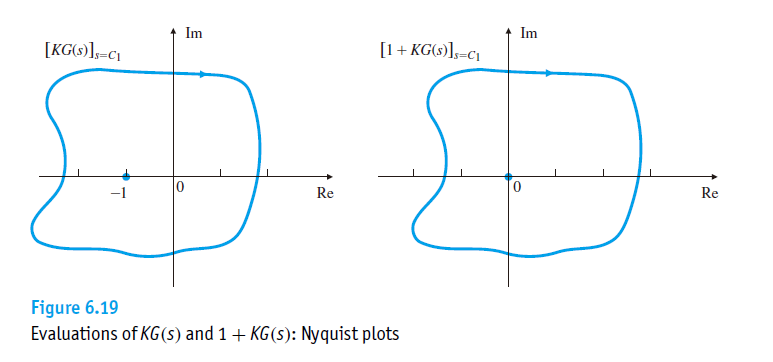
KG(s)幅相曲线绕过(-1,0j) 的净圈数我们记为

，顺时针则

为正。右半平面F(s)的零点数为

，极点数为

。则Z个零点会使得KG(s)顺时针绕(-1,0j) Z圈，P个极点使得KG(s)逆时针绕过(-1,0j) P圈。所以就有了，

F(s)的零点数Z就是右半平面的闭环极点数（不稳定闭环极点），P就是KG在右半平面的开环极点（不稳定开环极点）。于是

即：KG(s)对应的闭环系统在RHP处不稳定极点数Z等于幅相曲线绕过（-1,0j）的顺时针净圈数N和开环不稳定极点数P之和。Z=0则闭环系统在RHP的极点数为0，则系统稳定。

KG(s)的幅相频率特性曲线一般称为奈奎斯特图Nyquist plot或者极坐标图polar plot，因为它把频率特性的实部和虚部都画出来了。Nyquist plot是有方向的，并且是关于实轴对称的，当

从

到

变化时有一半的曲线，另一半曲线只需要关于实轴对称作图即可。当KG(s)中含有纯积分环节时，需要补作曲线，具体还是要参考教材，不细说了。如今采用MATLAB的NYQUIST命令就可以轻松画出KG(s)的Nyquist plot。

Nyquist plot也可以用来确定什么样的K能够使得系统变得稳定，就像Root Locus一样。我们检查KG(s)包围-1的情况等价于G(s)包围-1/K的情况，于是我们便可以在实数轴上取不同的-1/K值，并检查G(s)的Nyquist plot了。

下面来自[1]这段话是对确定Nyquist稳定性步骤的总结：

3.判断稳定性实例

下面是来自[1]中的2个例子，用来巩固这里的结论。

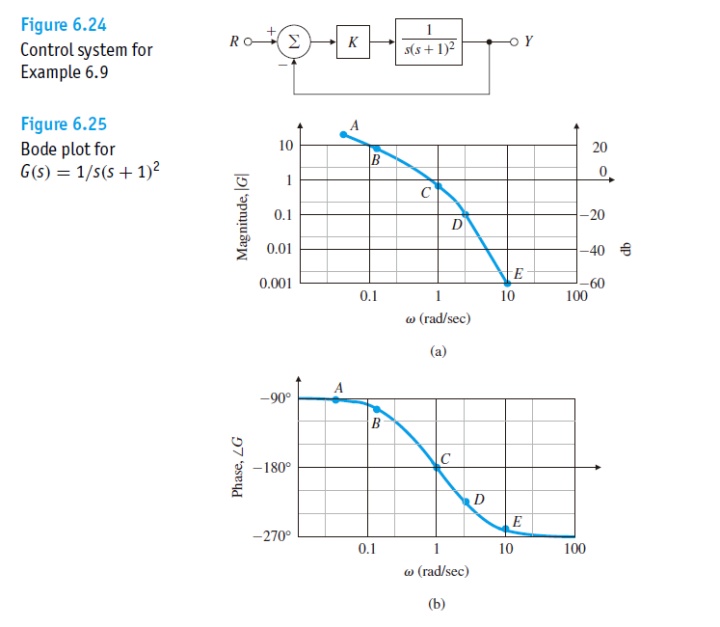
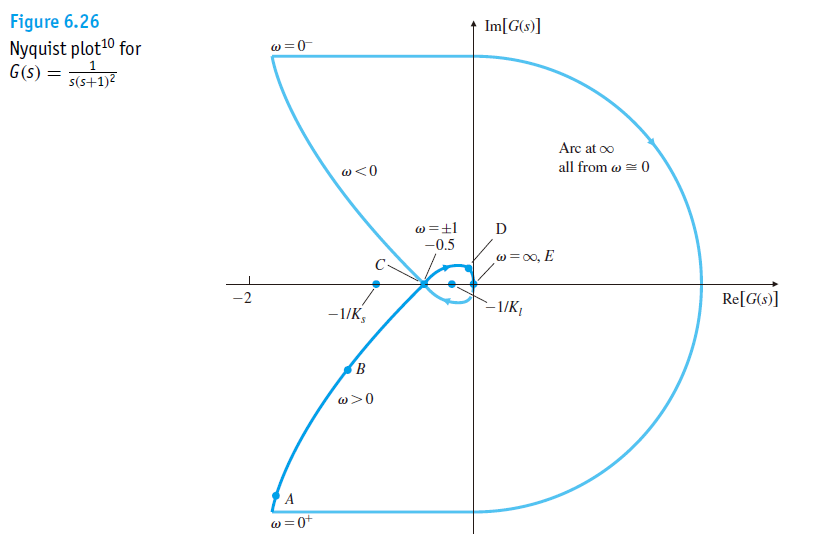
如果假设K>=0，那么在这里我们就可以用上面的结论，画出G(s)的Nyquist Plot从而确定什么样的K能够让系统稳定。

如果 K>2，那么-1/K则会在0到-0.5之间，那么此时N=2，P=0，则Z=N+P=2。意味着系统不稳定。如果K<2, 则曲线将不包围-1/K，于是N=0，P=0，Z=0，所有闭环特征值都在左半平面。

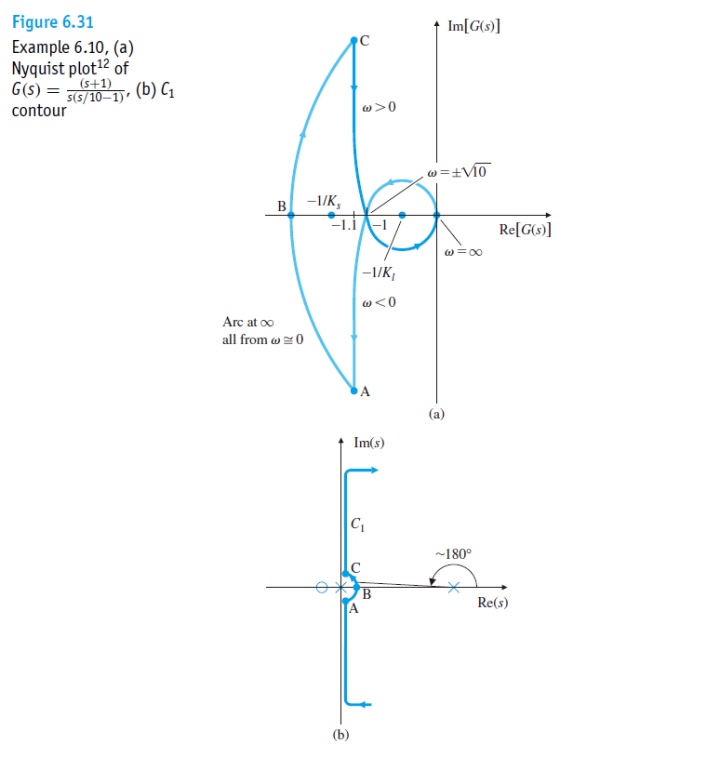
当 K >1 时，G(s)的曲线逆时针绕过-1/K，所以N=-1，且开环传递函数有不稳定极点s=10，于是P=1, Z=N+P=0，系统稳定。 当0<K<1 时，N=1，P=1，Z=2, 系统不稳定且有两个不稳定闭环极点。 如果K<0，那么-1/K就会出现在正实轴上，同样N=0，P=1，Z=N+P=1，于是有一个不稳定闭环极点，系统不稳定。

4.本篇小节

这篇中我们快速回顾了Nyquist Stability Criterion与Nyquist Plot的概念。实际上如果我们有了传递函数的表示式，判断闭环稳定性的一个好工具就是Root Locus Method。只要能够画出Root Locus，我们就根据根轨迹是否会前往右半平面和相对应的临街增益有一个掌握。当然这是出现在Nyquist Stability Criterion之后的事情了。

Nyquist Plot的优点在于其可以把整个频率范围内的频率特性都刻画在一张图上，而缺点就是原来Bode Plot中的每个环节的频率特性对整个系统的贡献就无法清晰得知了。对于下一篇中我们会讲到的相对稳定性和稳定裕度来说，Nyquist Plot呈现了比较完整地信息。

Reference：

[1] G.F. Franklin, J.D. Powell, A.Emami-Naeini, Feedback Control of Dynamic Systems, 7th Edition, 2014, Pearson