matlab 电路频率响应_MATLAB信号与系统——傅里叶变换、系统的频域分析

点击上方蓝字关注“公众号”

MATLAB傅里叶变换、系统的频域分析

当初学信号与系统，天书睡过去啊，一到考试心中mmp。理论的枯燥，有了MATLAB就生动形象啦。

1、学会用MATLAB实现连续时间信号傅里叶变换

2、学会用MATLAB分析LTI系统的频域特性

3、学会用MATLAB分析LTI系统的输出响应

壹

傅里叶变换的MATLAB求解

MATLAB的symbolic Math Toolbox 提供了直接求解傅里叶变换及逆变换的函数fourier()及ifourier()两者的调用格式如下。

01

Fourier 变换的调用格式

F=fourier(f)：它是符号函数f的fourier变换默认返回是关于w的函数。

F=fourier(f，v):它返回函数F是关于符号对象v的函数，而不是默认的w，即

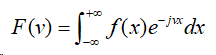
02

 Fourier逆变换的调用格式

f=ifourier(F):它是符号函数F的fourier逆变换，默认的独立变量为w，默认返回是关于x的函数。

f=ifourier(f,u):它的返回函数f是u的函数，而不是默认的x.

注意：在调用函数fourier()及ifourier()之前，要用syms命令对所用到的变量(如t,u,v,w)进行说明,即将这些变量说明成符号变量。

03

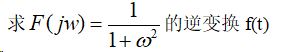
解： 可用MATLAB解决上述问题

syms t  w

ft=ifourier(1/(1+w^2),t)

贰

连续时间信号的频谱图

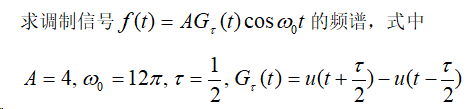
01

解：MATLAB程序如下所示

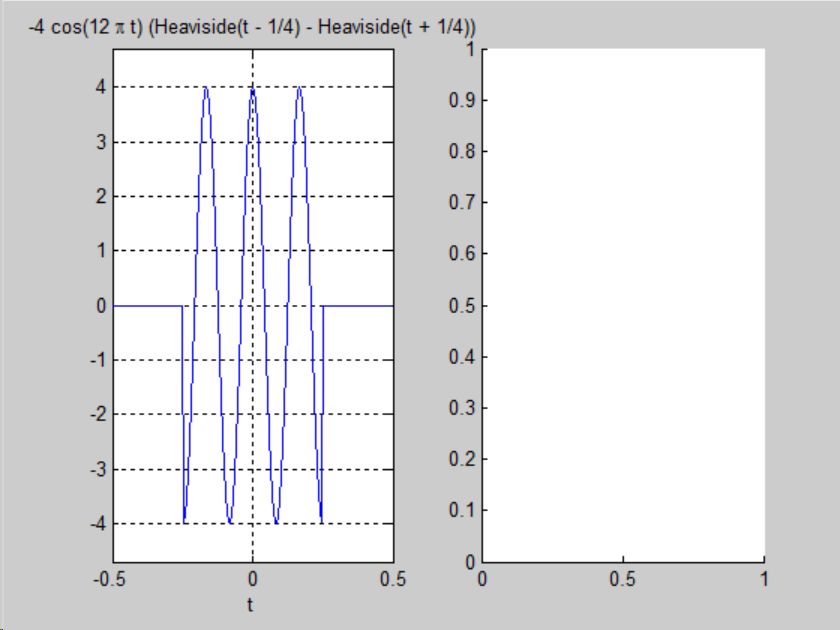
ft=sym('4*cos(2*pi*6*t)*(Heaviside(t+1/4)-Heaviside(t-1/4))');

Fw=simplify(fourier(ft))

subplot(121)

ezplot(ft,[-0.5 0.5]),grid on

subplot(122)

ezplot(abs(Fw),[-24*pi 24*pi]),grid

用MATLAB符号算法求傅里叶变换有一定局限，当信号不能用解析式表达时，会提示出错，这时用MATLAB的数值计算也可以求连续信号的傅里叶变换，计算原理是

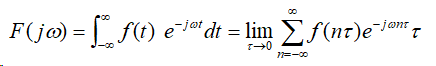
当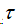足够小时，近似计算可满足要求。

若信号是时限的，或当时间大于某个给定值时，信号已衰减的很厉害，可以近似地看成时限信号时，n的取值就是有限的，设为N，有

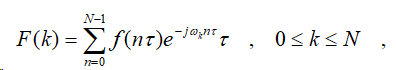
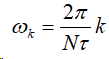是频率取样点

时间信号取样间隔应小于奈奎斯特取样时间间隔，若不是带限信号可根据计算精度要求确定一个频率 W0为信号的带宽。

02

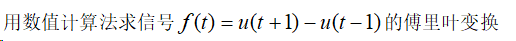
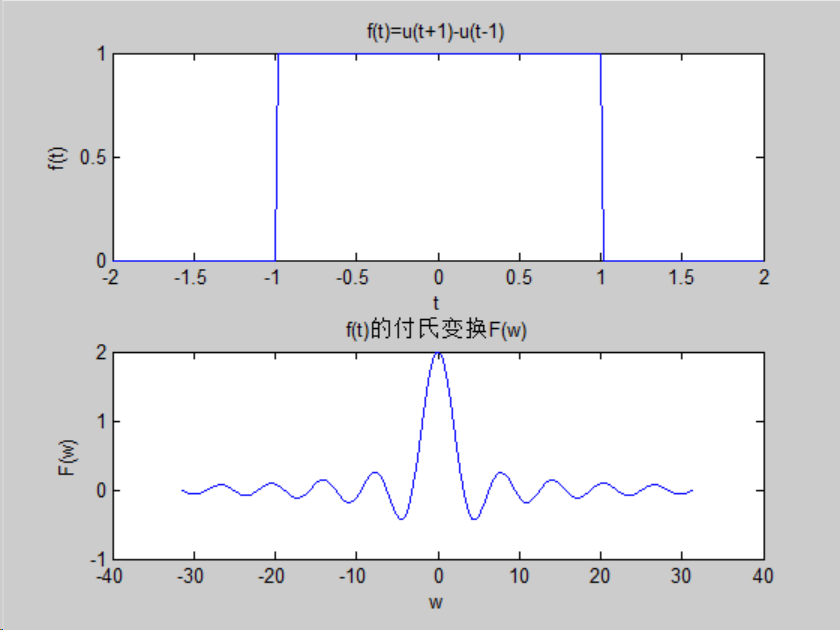
R=0.02;t=-2:R:2;

f=Heaviside(t+1)-Heaviside(t-1);

W1=2*pi*5;

N=500;k=0:N;W=k*W1/N;

F=f*exp(-j*t'*W)*R;

F=real(F);

W=[-fliplr(W),W(2:501)];

F=[fliplr(F),F(2:501)];

subplot(2,1,1);plot(t,f);

xlabel('t');ylabel('f(t)');

title('f(t)=u(t+1)-u(t-1)');

subplot(2,1,2);plot(W,F);

xlabel('w');ylabel('F(w)');

title('f(t)的付氏变换F(w)');

叁

用MATLAB分析LTI系统的频率特性

 当系统的频率响应H(jw)是jw的有理多项式时，有

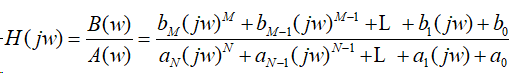
MATLAB信号处理工具箱提供的freqs函数可直接计算系统的频率响应的数值解。

其调用格式如下

H=freqs(b,a,w)

其中，a和b分别是H(jw)的分母和分子多项式的系数向量，w为形如w1:p:w2的向量，定义系统频率响应的频率范围，w1为频率起始值，w2为频率终止值,p为频率取样间隔。

H返回w所定义的频率点上，系统频率响应的样值。

01

例如，运行如下命令，计算0~2pi频率范围内以间隔0.5取样的系统频率响应的样值

a=[1  2  1];

b=[0  1];

h=freqs(b,a,0:0.5:2*pi)

02

三阶归一化的butterworth 低通滤波器的频率响应为

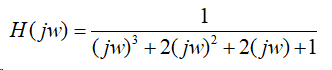
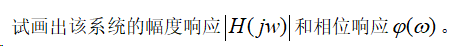
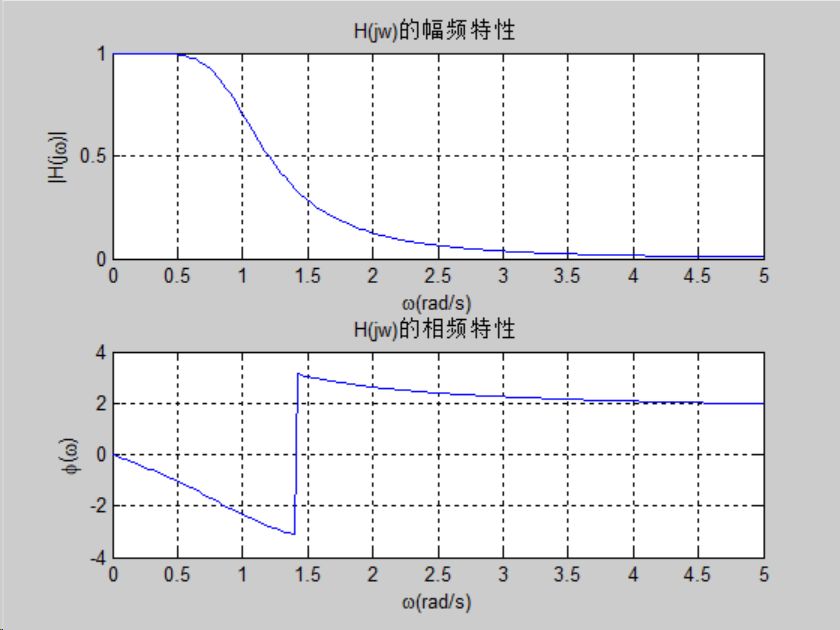
解 其MATLAB程序及响应的波形如下

w=0:0.025:5;

b=[1];a=[1,2,2,1];

H=freqs(b,a,w);

subplot(2,1,1);

plot(w,abs(H));grid;

xlabel('omega(rad/s)');

ylabel('|H(jomega)|');

title('H(jw)的幅频特性');

subplot(2,1,2);

plot(w,angle (H));grid;

xlabel('omega(rad/s)');

ylabel('phi(omega)');

title('H(jw)的相频特性');

肆

用MATLAB分析LTI系统的输出响应

已知一RC电路如图所示

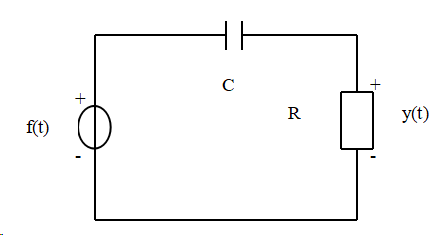
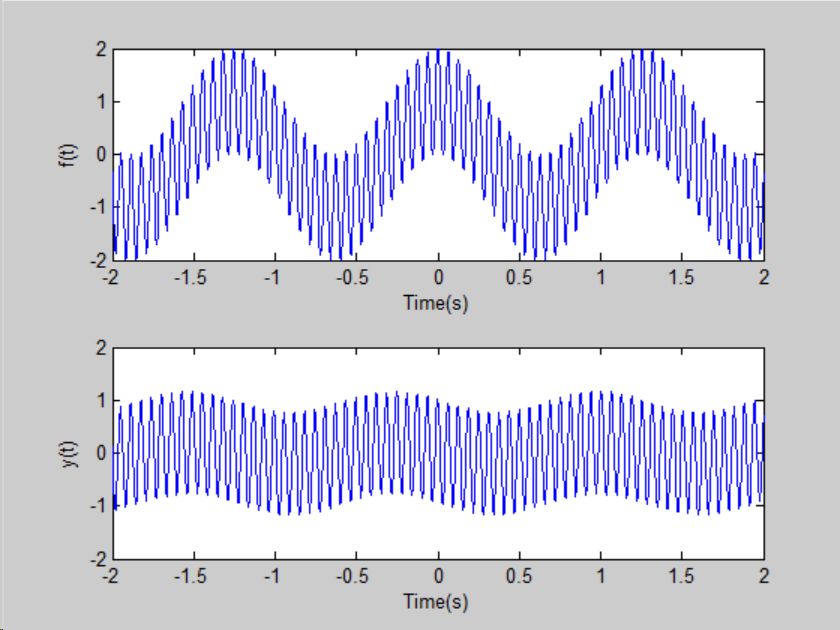
系统的输入电压为f(t)，输出信号为电阻两端的电压y(t).当RC=0.04，f(t)=cos5t+cos100t,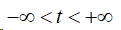试求该系统的响应y(t)

解 由图可知 ，该电路为一个微分电路，其频率响应为

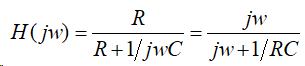
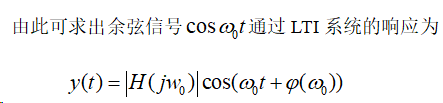
计算该系统响应的MATLAB程序及响应波形如下

RC=0.04;

t=linspace(-2,2,1024);

w1=5;w2=100;

H1=j*w1/(j*w1+1/RC);

H2=j*w2/(j*w2+1/RC);

f=cos(5*t)+cos(100*t);

y=abs(H1)*cos(w1*t+angle(H1))+ abs(H2)*cos(w2*t+angle(H2));

subplot(2,1,1);

plot(t,f);

ylabel('f(t)');

xlabel('Time(s)');

subplot(2,1,2);

plot(t,y);

ylabel('y(t)');

xlabel('Time(s)');

MATLAB各种版本下载，关注公众号即可获得链接。

扫码关注

不迷路