bpsk调制及解调实验_数字调制的性能

数字调制的性能有两个，错误率和中断率。错误率包括有误比特率，误符号率。中断率就是指瞬时信噪比小于门限的概率。对于AWGN信道和衰落信道的数字调制的性能肯定也是不一样的。所以为了衡量不同数字调制的性能，最好是给出误码率和信道信噪比之间的关系，最好是给出闭式解。

信噪比，符号信噪比，比特信噪比

信噪比（SNR）这个大家都很熟悉了。表示接受信号功率和噪声功率。功率本来就是信号能量在信号周期内的平均。加入基带复信号的带宽是

这个

一个符号或者一个比特的接收功率可以用

现在来定义符号信噪比：

看看符号信噪比和信噪比之间的关系，假设脉冲成形的脉冲满足：

而比特信噪比：

对于二进制调制，误比特率就是误符号率。而多进制调制则还有可能和比特到星座映射有关系，但是如果采用格雷码映射的话，在高信噪比的情况下（只会译码到相邻的星座点上），一个符号译错只会有一个比特错误。所以误码率

在实际中其实更关注误码率和比特信噪比之间的关系。因为真正影响用户体验的最小单位是比特。

误符号率、误码率的计算

用Q函数表示误符号率

这个过程还是有点复杂，我们先考虑最简单最基本的场景：AWGN信道，而且是在载波恢复和定时很准的理想情况下。

采用最大似然结构的接收机。假设信源发送消息是等概率的

联合界。

假设一个事件

这个不等式就是联合界。

对于

这就相当于噪声向量n到向量

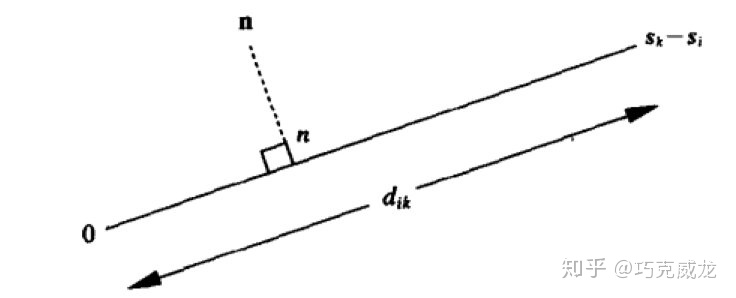
如上图所示，只有n 向量在

所以发送

整体的误码率联合界是：

看一下这个式子，第一个求和符号

Q函数是无闭式解的，但是Q函数有闭式上界。

当z 比较大时，这个上界是很紧的。所以继续放松得到：

所以我们得到了一个严格的松散界，我们来整理一下这个放松过程。第一次，联合界放松了。第二次，用星座点的最小距离来代替了所有的星座点之间的距离。第三次，用Q函数的上界代替了Q函数的值。所以一共三次放松。

也可以用最近邻近似来刻画误码率的上界。

前面的系数是指距离具有最小距离的那个星座点的星座点的个数，说的有点绕。就是说加入

最近邻近似，这个概念后面会经常用到。可以发现最近邻近似的误码率要小于上面放松了三次的松散界，不仅如此，他还比严格的联合界都略小。在高信噪比时，最近邻近似和误码率准确值是很接近的。这是因为信噪比在比较大时候，译码很难把码译到不相邻的星座点上去。也就是说，

联合界里面这些项占主导作用的是具备

特别的是，如果二元调制，星座点只有两个，那么联合界就变成了精确值。

我们上面提到的误码率、误符号率是一个东西。但是在实际系统的设计时，更加关心误比特率，误比特率可以影响上层网络协议以及端到端的性能。在常常使用格雷码映射以及在高信噪比的情况下，误比特率和误码率之间的关系可以用下式来近似：

Q函数的另一种等效表示方法

我们都知道Q函数是什么意思：

但是这个式子的特点是积分限是无穷大，整个式子没有闭式解，只有有一个上界，当这个

这个式子积分限是固定的，用这个式子计算误码率会简化计算，方便不少。

PSK在理想AWGN的误码率

BPSK

假设是在理想状态下的相干解调。BPSK就是一个符号就是一个bit，发0的信号对应于

显然的这个式子可以变一下形：

QPSK

QPSK是两路，每一路都是BPSK，所以一个QPSK符号有两个比特的信息量。那么这个想要正确发送一个符号，就必须两路都不能错。所以，

又因为：

这个值是精确值。

再来看看根据上一节的内容计算的这个近似值：

MPSK

这是MPSK的图：

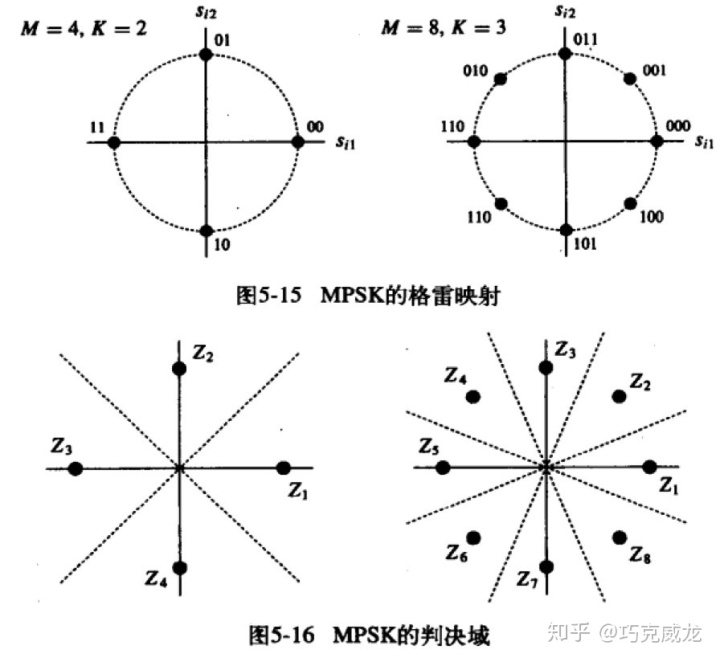
可以看到在MPSK中每一个符号的误码率都是一样的，那我们就来选（A，0）这个星座点来看误码率，在AWGN的信道中只有噪声才会带来误码，高斯噪声是一个个二维的高斯随机向量，现在给他换成极坐标

有兴趣的可以去推这个PDF。

但是我们只要这个角度

所以对于（A，0）这个符号而言，误符号率就是：

这个积分的式子太复杂了，当M超过4的时候并没有闭式解。只能用数值解法来求一个比较准确的解。

而MPSK误码率的最近邻近似：

因为MPSK两个星座点之间的最近距离是：

举一个例子增加一下感性的认识：

对于比特信噪比是15dB 的8PSK和16PSK，他们的误比特率事多少？

显然16PSK的误码率要大很多，虽然传输速率变快了，但是付出的是误码率的代价，直观上16PSK星座点之间距离也更近，所以误码也更大。

MPAM和MQAM在理想AWGN的误码率

MPAM

对于PAM来讲，判决域是下面这个样子：

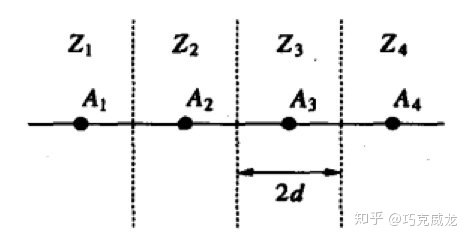
噪声叠加以后只要不超过判决域就不会产生误码，最外边的符号出错的

这里提一下：高斯随机变量

把误符号率写成和平均符号信噪比有关的形式：

MQAM

对于矩形的星座图，星座点的数量为

所以总的误符号率：

这是精确值。

采用最近邻近似的误码率取决于有最近邻点的个数。内点有四个，外点有两个或者三个。所以保守一点最近邻近似误码率为：

因为MQAM的平均能量是两路MPAM的平均能量：

而对于非矩形的星座图：一般难以求出误码率精确解，常用最近邻近似误码率。

误码率总结

可以看出相干解调所有误码率的式子都具备一下这种形式：

参数

衰落信道中误码率计算

在上面的高斯信道中不考虑路径损耗，阴影效应，多径什么的，接受信号功率就是发射功率和噪声功率的叠加。但是真实环境中衰落是无法避免地，也就意味着接受符号信噪比是一个随机过程。由此带来的误码率肯定也是随机的。而且信道变化的快慢的不同也对数字调制的影响不同，所以不同的场景得设置合适的评价指标。主要有中断率，平均错误率，中断率和平均错误率的结合。

如果信道的相干时间和一个码元的周期差不多，那就可以求一段时间内部的平均误码率就行了；如果信道很长时间都不变化，而且又处在深度衰落中，这种情况下课规定一定的中断率来允许一段时间不可通信；如果在一个码元周期里面衰落变化很快，接收端采用匹配滤波器可以平均掉，性能和AWGN信道是一样的。

中断率

中断率的定义：接收符号信噪比低于给定能容忍的信噪比的概率。

举例来说，假设信噪比为7dB 的视乎信号出现中断，那么设置

在上式中，给定中断率，门限值

平均误码率

当信道相干时间和码元周期差不多时，采用平均误码率作为性能指标。平均误码率可以用下面的积分形式来计算：

其中

以信号满足瑞利衰落分布为例：

在假设信号B带宽就是

根据这个关系把r的分布代进去得到：

其中，

在衰落信道中误比特率是和信噪比线性下降的，但是在AWGN的信道中是指数下降的。

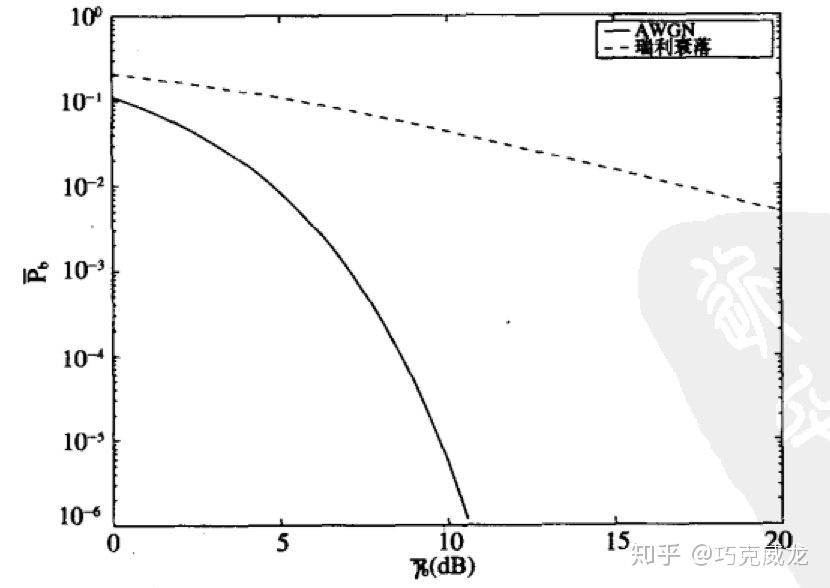
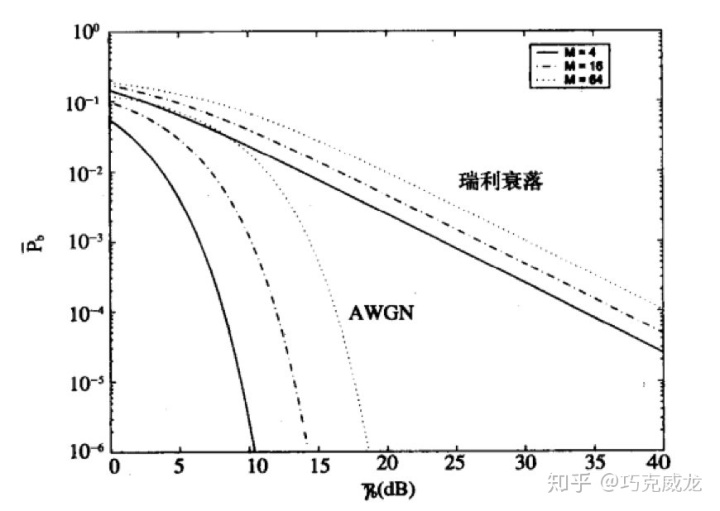
所以为了提升误码率而不过分的提升发射功率，常常采用分集、扩频、rake接收机来提升性能。当然信道的复杂性还会带来背景误码，比如多普勒频域和码间串扰，这些有兴趣的可以自己查阅相关资料。

总结

不知不觉写了这么多，误码率计算的确有点难，对数学要求比较高。但是最重要的就是怎么量化噪声对信号的影响，无非就是考虑噪声在判决域的积分。这是计算误码率最大的方法论。看似复杂，公式繁多，但都是纸老虎罢了。