文章目录
- 1. QPSK信号的调制原理
- 2. 双比特码元差分编码原理
- 3. DQPSK信号解调原理
- 3.1 相干解调原理
- 3.2 四次方环载波提取
- 3.3 Costas环载波提取
- 2.4 极性Costas环载波提取
- 3. DQPSK调制解调的MATLAN仿真
1. QPSK信号的调制原理
与多相ASK调制一样,相位调制也有多进制调制方式,其中最为广泛的是四相调制。四相调制也可分为四相绝对移相调制(也称为四相绝对相移键控,记为4PSK)和四相相对移相调制(又称为四相相对相移键控,记为4DPSK)两种,其中4DPSK也是未解决接收机对信号进行解调时产生的相位模糊而提出的一种调制方式。
4DPSK是由4PSK经过差分编码后调制的四相调制,因此我们先了解一下4PSK信号的调制原理。所谓四相绝对相移调制,是利用载波的四种不同相位来表征四种数字信息。因此,对于输入的二进制数字序列应该先进行分组,将每两个信息数字编为一组,然后根据其组合情况用四种不同的载波相位去表征它们。由于每一种载波相位代表两比特信息,故每个码元(四进制码元)常被称为双比特码元,并把组成双比特码元的前一信息比特用A代表,后一信息比特用B代表。双比特码元中两个信息比特AB是按格雷码(即反射码)排列的,因此,在接收端检测时,如果出现相邻相位判决错误,只造成一比特的差错,有利于提高传输的可靠性。
4PSK信号载波的相位 φ k varphi _{k} φk与双比特码元的对应关系通常有两种:一种为AB=00对应0°相位,AB=10对应90°相位,AB=11对应180°相位,AB=01对应270°相位;另一种为AB=00对应225°相位,AB=10对应315°相位,AB=11对应45°相位,AB=01对应135°相位.
显然,四相绝对相移调制可以看成两个正交的绝对相移调制的合成,且其中每一个二相调制都具有相同的基带调制波形。因此,4PSK也被称为正交相移键控(Quadrature Phase Shift Keying,QPSK)。当所有相位值都以等概率出现时,四相绝对相移调制波形的功率谱将是两个正交二相调制波形功率谱的合成。
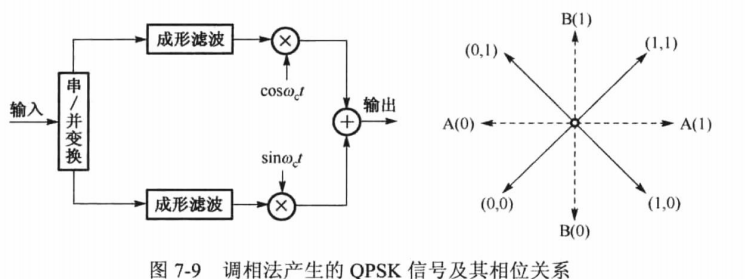
QPSK信号产生方法与2PSK信号一样,可以分为调相法和相位选择法。调相法产生4PSK信号的电路组成如下图(a)所示,图中,串/并转换器将输入的二进制数据序列依次分为两个并行的序列。设两个序列中的二进制数字分别为A和B,每一对AB称为一个双比特码元。双极性的A和B数字脉冲通过两个平衡调制器,对0°相载波
c
o
s
ω
c
t
cosomega_{c}t
cosωct及正交载波
s
i
n
ω
c
t
sinomega_{c}t
sinωct进行二相调制,得到下图(b)中的虚线相量;将两路输出叠加,即得到下图(b)中实线向量所示的四相信号。为了消除码间干扰,以及抑制主瓣带外频率分量功率的目的,通常会在平衡调制器之前增加一级成形滤波器。需要特别说明的是,下图(b)中,平衡调制器是对0°相载波及正交载波进行调制,由于两路信号叠加后信号的相位发生了
π
/
4
pi /4
π/4的偏移,因此采用相干解调时,相干载波实际上已转换成45°相位载波及其正交载波信号。
2. 双比特码元差分编码原理
对于二相相位调制来讲,为了得到2DPSK信号,可以先将绝对码变换成相对码,然后用相对码对载波进行绝对相移。同样,4DPSK信号也可以采用这种方法。先将输入的双比特码经过码型变换(差分编码),再用码型变换器输出的双比特码进行绝对相移。
所四相相对相移调制,也是利用前后码之间的相对相位变化来表示数字信息。若以前一码元相位作为参考。并令 Δ φ k Delta varphi _{k} Δφk为本码元与前一码元的初相差,则信息编码与载波相位变化关系与绝对相移调制相似。不过,此时绝对相移调制的相位为绝对相位 φ k varphi _{k} φk,相对相移调制的相位为相对相位 Δ φ k Delta varphi _{k} Δφk而已。当相对相位变化以等概率出现时,相对调相信号的功率谱密度与绝对调相信号的功率谱密度相同。
为进一步分析相对调相信号的载波相位与双比特数据的关系,我们将输入比特信息与载波相位直接的关系以列表形式给出:
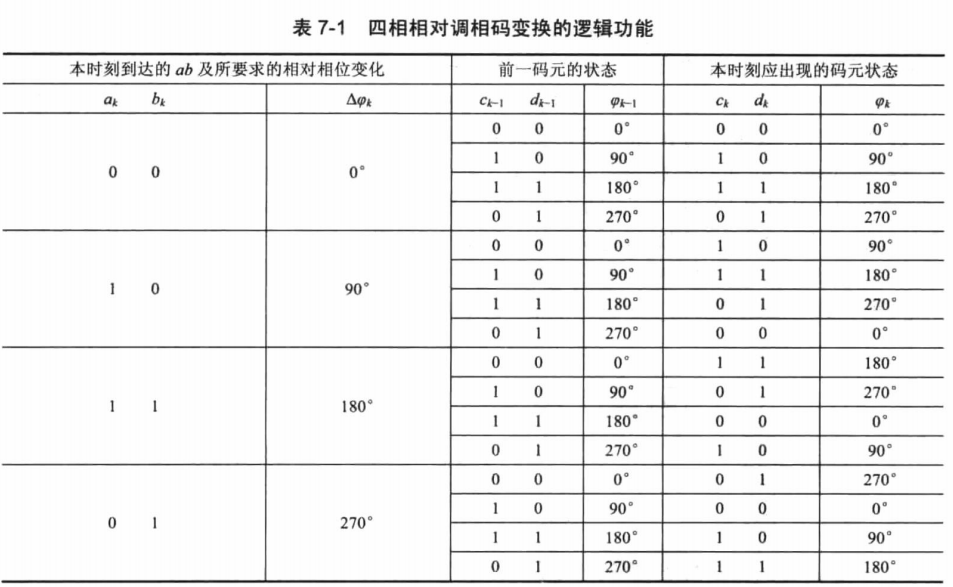
上表列出了绝对码转相对码的逻辑关系。在接收端,显然还需要将解调出的相对码转换为绝对码,即原始调制数据。接收端的差分解码器与发送端的解码器功能相反,且一一对应。假设解码器当前的输入数据为
c
k
、
d
k
c_{k}、d_{k}
ck、dk,前一码元输入数据为
c
k
−
1
、
d
k
−
1
c_{k-1}、d_{k-1}
ck−1、dk−1,输出的绝对码数据为
a
k
、
b
k
a_{k}、b_{k}
ak、bk,则根据编码器的规则,很容易获取解码器的转换关系。例如,当前后两个码元数据完全相同时(
c
k
=
c
k
−
1
、
d
k
=
d
k
−
1
c_{k}=c_{k-1}、d_{k}=d_{k-1}
ck=ck−1、dk=dk−1),则输出的绝对码
a
k
=
0
、
b
k
=
0
a_{k}=0、b_{k}=0
ak=0、bk=0;当前一码元(
c
k
−
1
=
0
、
d
k
−
1
=
0
c_{k-1}=0、d_{k-1}=0
ck−1=0、dk−1=0),当前码元
c
k
=
1
、
d
k
=
1
c_{k}=1、d_{k}=1
ck=1、dk=1时,则输出的绝对码
a
k
=
0
、
b
k
=
1
a_{k}=0、b_{k}=1
ak=0、bk=1.
第一种情况:前一码元
c
k
−
1
⊕
d
k
−
1
=
0
c_{k-1}oplus d_{k-1}=0
ck−1⊕dk−1=0时,解码器的输出有
a
k
=
c
k
⊕
c
k
−
1
,
b
k
=
d
k
⊕
d
k
−
1
a_{k}=c_{k}oplus c_{k-1},b_{k}=d_{k}oplus d_{k-1}
ak=ck⊕ck−1,bk=dk⊕dk−1;第二种情况:前一码元
c
k
−
1
⊕
d
k
−
1
=
1
c_{k-1}oplus d_{k-1}=1
ck−1⊕dk−1=1时,解码器的输出有
b
k
=
c
k
⊕
c
k
−
1
,
a
k
=
d
k
⊕
d
k
−
1
b_{k}=c_{k}oplus c_{k-1},a_{k}=d_{k}oplus d_{k-1}
bk=ck⊕ck−1,ak=dk⊕dk−1。因此,我们很容易分析出解码器的组成结构如下图所示。
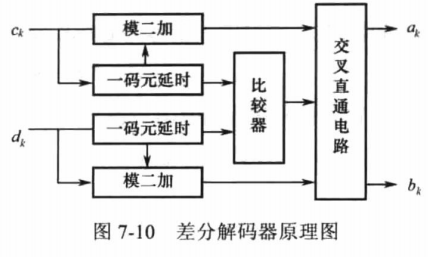
两路输入信号
c
k
、
d
k
c_{k}、d_{k}
ck、dk分别与前一码元信号
c
k
−
1
、
d
k
−
1
c_{k-1}、d_{k-1}
ck−1、dk−1模二相加,完成
c
k
⊕
c
k
−
1
c_{k}oplus c_{k-1}
ck⊕ck−1及
d
k
⊕
d
k
−
1
d_{k}oplus d_{k-1}
dk⊕dk−1的运算,然后比较前一码元信号
c
k
−
1
、
d
k
−
1
c_{k-1}、d_{k-1}
ck−1、dk−1的极性,并用极性比较器输出的信号去控制交叉直通电路。当
c
k
−
1
⊕
d
k
−
1
=
0
c_{k-1}oplus d_{k-1}=0
ck−1⊕dk−1=0时,交叉直通电路处于直通状态,即把
c
k
⊕
c
k
−
1
c_{k}oplus c_{k-1}
ck⊕ck−1作为
a
k
a_{k}
ak的输出,而把
d
k
⊕
d
k
−
1
d_{k}oplus d_{k-1}
dk⊕dk−1作为
b
k
b_{k}
bk的输出;反之,当
c
k
−
1
⊕
d
k
−
1
=
1
c_{k-1}oplus d_{k-1}=1
ck−1⊕dk−1=1时,交叉直通电路处于交叉状态,即把
c
k
⊕
c
k
−
1
c_{k}oplus c_{k-1}
ck⊕ck−1作为
b
k
b_{k}
bk的输出,而把
d
k
⊕
d
k
−
1
d_{k}oplus d_{k-1}
dk⊕dk−1作为
a
k
a_{k}
ak的输出;
3. DQPSK信号解调原理
3.1 相干解调原理
与PSK信号一样,QPSK只能采用相干解调方法,而DQPSK则可以采用最常用的差分解调方法(非相干解调)。
DQPSK解调与QPSK解调相比,只是QPSK解调后的数据进行一次差分解码即可。由于QPSK可以看出两路正交PSK信号的合成信号,因此不难得出DQPSK信号的相干解调原理框图,如下图所示
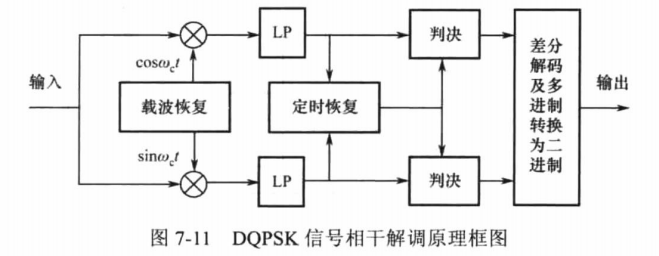
相干解调方法的关键在于获取相干载波及准确的定位定时信息。上图中,同相正交支路解调后的数据是二进制数据,因此位定时信息仍然可以采用锁相环位同步技术实现。载波提取的方法较多,常有的有四次方环法、四相Costas环法和极性Costas环法等。
3.2 四次方环载波提取
接收端接收到的抑制载波的QPSK调制信号本身无载波分量,然而经过非线性变换却能产生载波的倍频分量,用锁相环将其提取出来,经过分频就可得到相干载波。
设输入信号为QPSK调制信号
s
(
t
)
=
I
(
t
)
c
o
s
(
ω
c
t
+
φ
0
)
−
Q
(
t
)
s
i
n
(
ω
c
t
+
φ
0
)
s(t)=I(t)cos(omega _{c}t+varphi _{0})-Q(t)sin(omega _{c}t+varphi _{0})
s(t)=I(t)cos(ωct+φ0)−Q(t)sin(ωct+φ0)
对输入信号进行四次方后得到
s
(
t
)
4
=
[
I
2
(
t
)
c
o
s
2
(
ω
c
t
+
φ
0
)
−
I
(
t
)
Q
(
t
)
s
i
n
(
2
ω
c
t
+
2
φ
0
)
−
Q
2
(
t
)
s
i
n
2
(
ω
c
t
+
φ
0
)
]
2
=
{
I
2
(
t
)
+
Q
2
(
t
)
2
+
1
2
[
I
2
(
t
)
−
Q
2
(
t
)
]
c
o
s
(
2
ω
c
t
+
2
φ
0
)
−
I
(
t
)
Q
(
t
)
s
i
n
(
2
ω
c
t
+
2
φ
0
)
}
2
s(t)^{4}=[I^{2}(t)cos^{2}(omega _{c}t+varphi _{0})-I(t)Q(t)sin(2omega _{c}t+2varphi _{0})-Q^{2}(t)sin^{2}(omega _{c}t+varphi _{0})]^{2}=left { frac{I^{2}(t)+Q^{2}(t)}{2} +frac{1}{2}[I^{2}(t)-Q^{2}(t)]cos(2omega _{c}t+2varphi _{0})-I(t)Q(t)sin(2omega _{c}t+2varphi _{0})right }^{2}
s(t)4=[I2(t)cos2(ωct+φ0)−I(t)Q(t)sin(2ωct+2φ0)−Q2(t)sin2(ωct+φ0)]2={2I2(t)+Q2(t)+21[I2(t)−Q2(t)]cos(2ωct+2φ0)−I(t)Q(t)sin(2ωct+2φ0)}2
由于
I
(
t
)
、
Q
(
t
)
I(t)、Q(t)
I(t)、Q(t)的取值为
±
1
pm 1
±1,因此上式可简化为
s
(
t
)
4
=
{
1
−
I
(
t
)
Q
(
t
)
s
i
n
(
2
ω
c
t
+
2
φ
0
)
}
2
=
1
−
2
I
(
t
)
Q
(
t
)
s
i
n
(
2
ω
c
t
+
2
φ
0
)
+
I
2
(
t
)
Q
2
(
t
)
s
i
n
2
(
2
ω
c
t
+
2
φ
0
)
=
3
2
−
I
(
t
)
Q
(
t
)
s
i
n
(
2
ω
c
t
+
2
φ
0
)
−
1
2
c
o
s
(
4
ω
c
t
+
4
φ
0
)
s(t)^{4}=left { 1-I(t)Q(t)sin(2omega _{c}t+2varphi _{0}) right }^{2}=1-2I(t)Q(t)sin(2omega _{c}t+2varphi _{0})+I^{2}(t)Q^{2}(t)sin^{2}(2omega _{c}t+2varphi _{0})=frac{3}{2}-I(t)Q(t)sin(2omega _{c}t+2varphi _{0})-frac{1}{2}cos(4omega _{c}t+4varphi _{0})
s(t)4={1−I(t)Q(t)sin(2ωct+2φ0)}2=1−2I(t)Q(t)sin(2ωct+2φ0)+I2(t)Q2(t)sin2(2ωct+2φ0)=23−I(t)Q(t)sin(2ωct+2φ0)−21cos(4ωct+4φ0)
上式中已包含有载波的4倍频分量,用一个窄带滤波器将其滤除,再经过4分频即可得到所需的相干载波。当然,也能利用锁相环的跟踪功能提取相干载波。
3.3 Costas环载波提取
对于四相PSK调制来讲,仍然可以采用Costas环来解调,只是其鉴相器结构稍有不同,其组成原理图如下
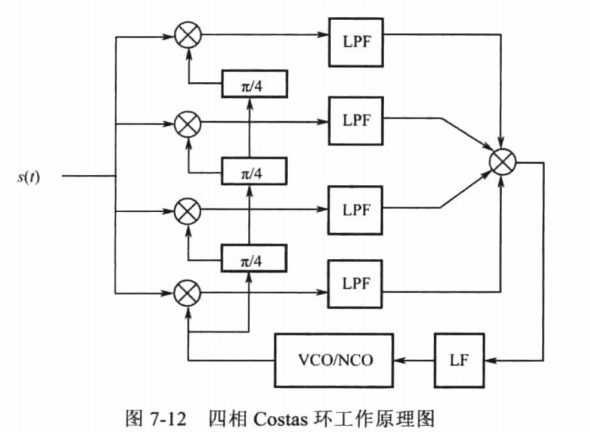
设VCO输出的本振信号
V
v
c
o
(
t
)
=
−
s
i
n
[
ω
c
t
+
θ
e
(
t
)
]
V_{vco}(t)=-sin[omega_{c}t+theta_{e}(t)]
Vvco(t)=−sin[ωct+θe(t)]
四路乘法及滤波后输出的信号分别为
y
1
(
t
)
=
−
I
(
t
)
2
c
o
s
[
θ
e
(
t
)
−
π
/
4
]
+
Q
(
t
)
2
s
i
n
[
θ
e
(
t
)
−
π
/
4
]
y_{1}(t)=-frac{I(t)}{2}cos[theta_{e}(t)-pi/4]+frac{Q(t)}{2}sin[theta_{e}(t)-pi/4]
y1(t)=−2I(t)cos[θe(t)−π/4]+2Q(t)sin[θe(t)−π/4]
y
2
(
t
)
=
−
I
(
t
)
2
c
o
s
[
θ
e
(
t
)
]
+
Q
(
t
)
2
s
i
n
[
θ
e
(
t
)
]
y_{2}(t)=-frac{I(t)}{2}cos[theta_{e}(t)]+frac{Q(t)}{2}sin[theta_{e}(t)]
y2(t)=−2I(t)cos[θe(t)]+2Q(t)sin[θe(t)]
y
3
(
t
)
=
I
(
t
)
2
s
i
n
[
θ
e
(
t
)
−
π
/
4
]
+
Q
(
t
)
2
c
o
s
[
θ
e
(
t
)
−
π
/
4
]
y_{3}(t)=frac{I(t)}{2}sin[theta_{e}(t)-pi/4]+frac{Q(t)}{2}cos[theta_{e}(t)-pi/4]
y3(t)=2I(t)sin[θe(t)−π/4]+2Q(t)cos[θe(t)−π/4]
y
4
(
t
)
=
−
I
(
t
)
2
s
i
n
[
θ
e
(
t
)
]
+
Q
(
t
)
2
c
o
s
[
θ
e
(
t
)
]
y_{4}(t)=-frac{I(t)}{2}sin[theta_{e}(t)]+frac{Q(t)}{2}cos[theta_{e}(t)]
y4(t)=−2I(t)sin[θe(t)]+2Q(t)cos[θe(t)]
四路信号相乘,即得到等效鉴相器的输出
V
c
(
t
)
=
y
1
(
t
)
y
2
(
t
)
y
3
(
t
)
y
4
(
t
)
=
I
2
(
t
)
Q
2
(
t
)
32
s
i
n
[
4
θ
e
(
t
)
]
=
1
32
s
i
n
[
4
θ
e
(
t
)
]
V_{c}(t)=y_{1}(t)y_{2}(t)y_{3}(t)y_{4}(t)=frac{I^{2}(t)Q^{2}(t)}{32}sin[4theta_{e}(t)]=frac{1}{32}sin[4theta_{e}(t)]
Vc(t)=y1(t)y2(t)y3(t)y4(t)=32I2(t)Q2(t)sin[4θe(t)]=321sin[4θe(t)]
时钟,
θ
e
(
t
)
theta_{e}(t)
θe(t)为相位误差,显然所提取的载波相位具有四重相位模糊度,在锁定状态下,
θ
e
(
t
)
theta_{e}(t)
θe(t)可能处于
0
、
π
/
2
、
π
、
3
π
/
2
0、pi /2、pi、3pi /2
0、π/2、π、3π/2附近。在接收端,由于采用了差分编码处理,可以有效克服相位模糊对解调判决的影响。
2.4 极性Costas环载波提取
判决反馈环的工作原理是对先接收信号进行相干预解调,将解调出来的信号去抵消接收信号的调制信息,由此来得到误差电压,实现载波提取。对于QPSK信号来讲,可以将判决反馈环简化为一个修正的Costas环,也称为极性Costas环,其原理框图如下所示
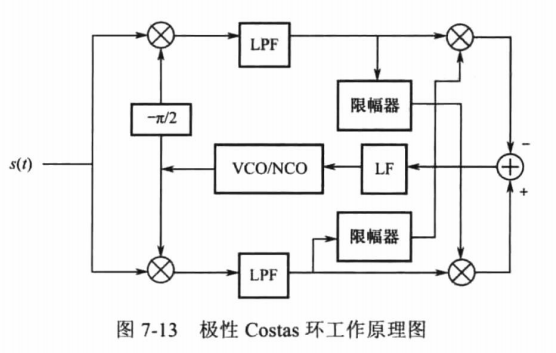
对于输入信号
s
(
t
)
s(t)
s(t)及VCO本振输出信号
V
V
C
O
(
t
)
V_{VCO}(t)
VVCO(t),环路中两路乘法及低通滤波器输出的信号分别为
y
1
(
t
)
=
I
(
t
)
2
c
o
s
[
θ
e
(
t
)
]
−
Q
(
t
)
2
s
i
n
[
θ
e
(
t
)
]
y_{1}(t)=frac{I(t)}{2}cos[theta_{e}(t)]-frac{Q(t)}{2}sin[theta_{e}(t)]
y1(t)=2I(t)cos[θe(t)]−2Q(t)sin[θe(t)]
y
2
(
t
)
=
I
(
t
)
2
s
i
n
[
θ
e
(
t
)
]
+
Q
(
t
)
2
c
o
s
[
θ
e
(
t
)
]
y_{2}(t)=frac{I(t)}{2}sin[theta_{e}(t)]+frac{Q(t)}{2}cos[theta_{e}(t)]
y2(t)=2I(t)sin[θe(t)]+2Q(t)cos[θe(t)]
等效鉴相器的输出为
V
c
(
t
)
=
y
2
(
t
)
×
s
i
g
n
[
y
1
(
t
)
]
−
y
1
(
t
)
×
s
i
g
n
[
y
2
(
t
)
]
V_{c}(t)=y_{2}(t)times sign[y_{1}(t)]-y_{1}(t)times sign[y_{2}(t)]
Vc(t)=y2(t)×sign[y1(t)]−y1(t)×sign[y2(t)]
等效鉴相特性为
D
[
θ
e
(
t
)
]
=
{
K
d
s
i
n
[
θ
e
(
t
)
]
,
−
π
/
4
⩽
θ
e
(
t
)
⩽
π
/
4
−
K
d
c
o
s
[
θ
e
(
t
)
]
,
π
/
4
⩽
θ
e
(
t
)
⩽
3
π
/
4
−
K
d
s
i
n
[
θ
e
(
t
)
]
,
3
π
/
4
⩽
θ
e
(
t
)
⩽
5
π
/
4
K
d
c
o
s
[
θ
e
(
t
)
]
,
5
π
/
4
⩽
θ
e
(
t
)
⩽
7
π
/
4
D[theta_{e}(t)]=left{begin{matrix} K_{d}sin[theta_{e}(t)], &-pi/4leqslant theta_{e}(t)leqslant pi/4 \ -K_{d}cos[theta_{e}(t)], &pi/4leqslant theta_{e}(t)leqslant 3pi/4 \ -K_{d}sin[theta_{e}(t)], &3pi/4leqslant theta_{e}(t)leqslant 5pi/4 \ K_{d}cos[theta_{e}(t)], &5pi/4leqslant theta_{e}(t)leqslant 7pi/4 end{matrix}right.
D[θe(t)]=⎩⎪⎪⎨⎪⎪⎧Kdsin[θe(t)],−Kdcos[θe(t)],−Kdsin[θe(t)],Kdcos[θe(t)],−π/4⩽θe(t)⩽π/4π/4⩽θe(t)⩽3π/43π/4⩽θe(t)⩽5π/45π/4⩽θe(t)⩽7π/4
式中,
θ
e
(
t
)
theta_{e}(t)
θe(t)为相位误差,鉴相特性曲线以
π
/
2
pi/2
π/2为周期,锁定状态仍然可能处于
θ
e
(
t
)
theta_{e}(t)
θe(t)可能处于
0
、
π
/
2
、
π
、
3
π
/
2
0、pi /2、pi、3pi /2
0、π/2、π、3π/2附近,即载波相位提取存在四重不确定性。
在整个环路中,跟踪误差为
Δ
θ
=
(
1
/
4
)
s
i
n
−
1
(
12
2
π
σ
3
)
∣
f
0
−
f
∣
/
K
0
A
4
Delta theta=(1/4)sin^{-1}(12sqrt{2pi}sigma ^{3})left | f_{0}-f right |/K_{0}A^{4}
Δθ=(1/4)sin−1(122πσ3)∣f0−f∣/K0A4
式中,
f
0
f_{0}
f0为VCO的自由振荡频率,f为输入信号频率,
K
0
K_{0}
K0为VCO灵敏度,
σ
sigma
σ为窄带高斯白噪声均方根值,A为输入信号均值。可以看出,如果希望设计的载波环有好的跟踪性能,那么
K
0
A
4
K_{0}A^{4}
K0A4要大,特别是在低信噪比环境下设计的VCO/NCO灵敏度要高。
比较集中载波提取环路,可以看出极性Costas环路的结构更为简单,且不需要乘法运算,因此更有利于FPGA实现。
3. DQPSK调制解调的MATLAN仿真
条件:仿真双比特绝对码转换为相对码的过程;采用调相法产生DQPSK信号;基带信号符号速率 R b = 1 M b p s R_{b}=1Mbps Rb=1Mbps;成形滤波去的滚降因子 α = 0.8 alpha=0.8 α=0.8;载波信号频率 f c = 2 M H z f_{c}=2MHz fc=2MHz;采样频率 f s = 8 R b f_{s}=8R_{b} fs=8Rb;
ps=1*10^6; %码速率为1MHz
a=0.8; %成形滤波器系数
B=(1+a)*ps; %中频信号处理带宽
Fs=8*10^6; %采样速率
fc=2*10^6; %载波频率
N=24000; %仿真数据的长度
t=0:1/Fs:(N*Fs/ps-1)/Fs;%产生长度为N,频率为fs的时间序列
s=randint(N,1,4); %产生随机四进制数据作为原始数据
%s=ones(N,1)*3;
%将绝对码变换为相对码
ds=zeros(1,N);
for i=2:N
if s(i)==0
ds(i)=ds(i-1);
elseif s(i)==1
if ds(i-1)==0
ds(i)=1;
elseif ds(i-1)==2
ds(i)=0;
elseif ds(i-1)==3
ds(i)=2;
elseif ds(i-1)==1
ds(i)=3;
end
elseif s(i)==2
if ds(i-1)==0
ds(i)=2;
elseif ds(i-1)==2
ds(i)=3;
elseif ds(i-1)==3
ds(i)=1;
elseif ds(i-1)==1
ds(i)=0;
end
elseif s(i)==3
if ds(i-1)==0
ds(i)=3;
elseif ds(i-1)==2
ds(i)=1;
elseif ds(i-1)==3
ds(i)=0;
elseif ds(i-1)==1
ds(i)=2;
end
end
end
%将四进制数据分成同相正交两路数据的双极性码
%i支路在低位,q支路在高位
ds_i=zeros(1,N);
ds_q=zeros(1,N);
for i=1:N
if ds(i)==0
ds_i(i)=1;ds_q(i)=1;
elseif ds(i)==1
ds_i(i)=-1;ds_q(i)=1;
elseif ds(i)==2
ds_i(i)=1;ds_q(i)=-1;
elseif ds(i)==3
ds_i(i)=-1;ds_q(i)=-1;
end
end
%对相对码数据以Fs频率采样
Ads_i=upsample(ds_i,Fs/ps);
Ads_q=upsample(ds_q,Fs/ps);
%加噪声
% SNR=20;
% Ads_i=awgn(Ads_i,SNR);
% Ads_q=awgn(Ads_q,SNR);
%设计平方升余弦滤波器
n_T=[-2 2];
rate=Fs/ps;
T=1;
Shape_b = rcosfir(a,n_T,rate,T);%figure(4);freqz(Shape_b)
%对采样后的数据进行升余弦滤波;
rcos_Ads_i=filter(Shape_b,1,Ads_i);
rcos_Ads_q=filter(Shape_b,1,Ads_q);
%产生同相正交两路载频信号
f0_i=sin(2*pi*fc*t);
f0_q=cos(2*pi*fc*t);
%产生DQPSK已调信号
dqpsk=rcos_Ads_i.*f0_i+rcos_Ads_q.*f0_q;
%与相干载波相乘,实现相干解调
demod_mult_i=dqpsk.*f0_i;
demod_mult_q=dqpsk.*f0_q;
%设计接收端低通滤波器
fc=[ps 3.1*10^6]; %过渡带
mag=[1 0]; %窗函数的理想滤波器幅度
dev=[0.01 0.01]; %纹波
[n,wn,beta,ftype]=kaiserord(fc,mag,dev,Fs) %获取凯塞窗参数
fpm=[0 fc(1)*2/Fs fc(2)*2/Fs 1]; %firpm函数的频段向量
magpm=[1 1 0 0]; %firpm函数的幅值向量
rec_lpf=firpm(n,fpm,magpm);
%对乘法运算后的同相正交支路滤波
demod_lpf_i=filter(rec_lpf,1,demod_mult_i);
demod_lpf_q=filter(rec_lpf,1,demod_mult_q);
%绘制DQPSK信号频谱、DQPSK信号时域波形
figure(1)
m_dqpsk=20*log10(abs(fft(dqpsk,1024)));m_dqpsk=m_dqpsk-max(m_dqpsk);
%设置幅频响应的横坐标单位为MHz
x_f=[0:(Fs/length(m_dqpsk)):Fs/2];x_f=x_f/10^6;
%只显示正频率部分的幅频响应
mdqpsk=m_dqpsk(1:length(x_f));
%设置时域波表的横坐标单位为us
Len=100;%设置时域波形显示的点数
x_t=1:Len;%产生长度为Len的时间序列
x_t=x_t/Fs*10^6;
%显示所需的频谱及时域波形
subplot(211); plot(x_f,mdqpsk);
legend('相对码信号频谱');
xlabel('频率(MHz)');ylabel('幅度(dB)');grid on;
subplot(212);plot(x_t,dqpsk(101:Len+100));
legend('DQPSK时域信号波形');
xlabel('时间(us)');ylabel('幅度(V)');grid on;
%绘制解调前后的原始基带数据
figure(2)
Len=100;%设置时域波形显示的点数
x_t=1:Len;%产生长度为Len的时间序列
x_t=x_t/ps*10^6;
%绘制DPSK解调前后时域波形
subplot(311) %原始绝对码及相对码波形
plot(x_t,s(1:Len),'-',x_t,ds(1:Len)+3.5,'-');grid on;
legend('原始四进制绝对码波形','原始四进制相对码波形');
xlabel('时间(us)');ylabel('幅度(V)');
subplot(312) %解调后的同相支路基带波形
Len=800;%设置时域波形显示的点数
x_t=1:Len;%产生长度为Len的时间序列
x_t=x_t/ps*10^6;
plot(x_t,demod_lpf_i(1:Len));grid on;
legend('解调后的同相支路基带波形');
xlabel('时间(us)');ylabel('幅度(V)');
subplot(313) %解调后的正交支路基带波形
plot(x_t,demod_lpf_q(1:Len)');grid on;
legend('解调后的正交支路基带波形');
xlabel('时间(us)');ylabel('幅度(V)');
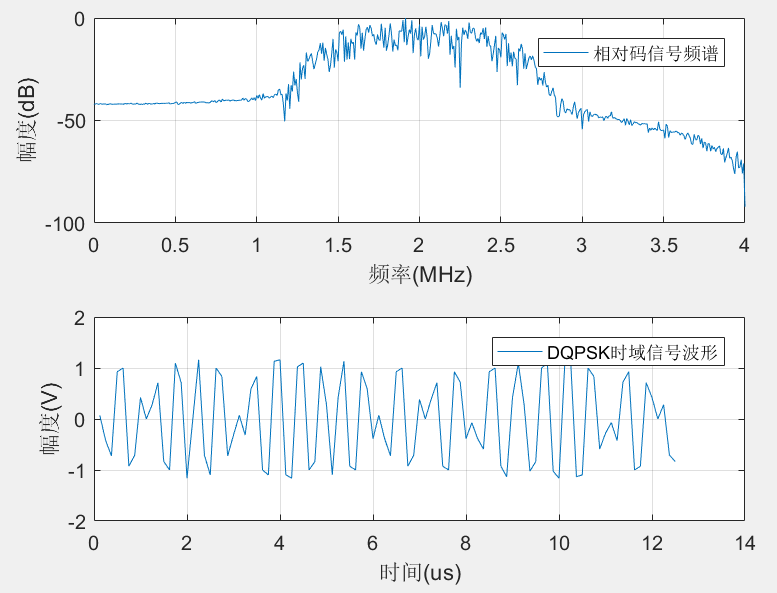
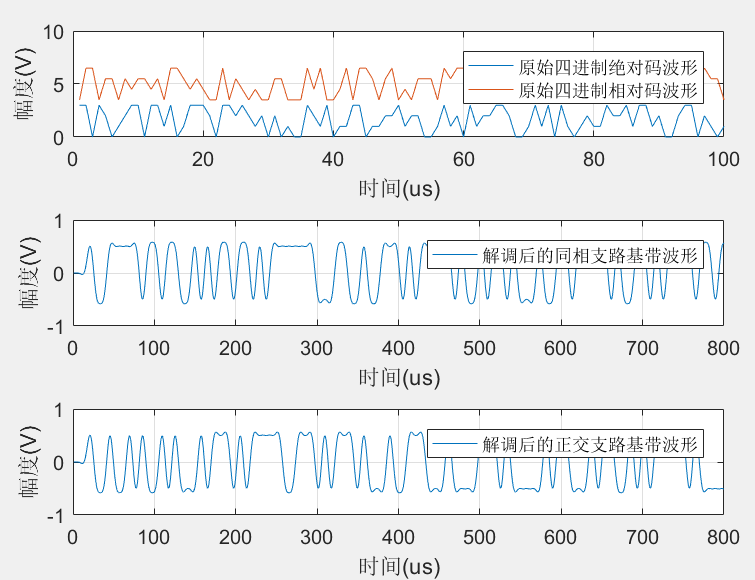
DQPSK信号的频谱及时域波形如下图所示,DQPSK调试数据及解调后的基带时序波形如下图所示
最后
以上就是和谐高山最近收集整理的关于DQPSK调制解调1. QPSK信号的调制原理2. 双比特码元差分编码原理3. DQPSK信号解调原理3. DQPSK调制解调的MATLAN仿真的全部内容,更多相关DQPSK调制解调1.内容请搜索靠谱客的其他文章。








发表评论 取消回复