前言

本节介绍了正交幅度调制QAM，它与PSK的区别在于：当M增大时，点之间的距离变大，所以误码率会上升，所以QAM的误码率要由于PSK。其中许多内容是与前面的幅度调制类似的。

一、调制和解调的过程

QAM信号使用两个正交载波cos(wt)和sin(wt)，其中每个都被一个独立的信息比特序列所调制。相应的信号波形可以表示为：

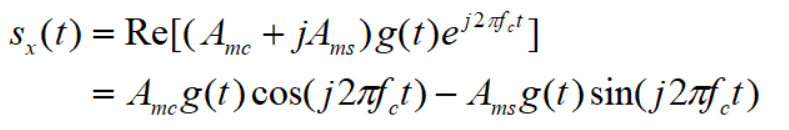
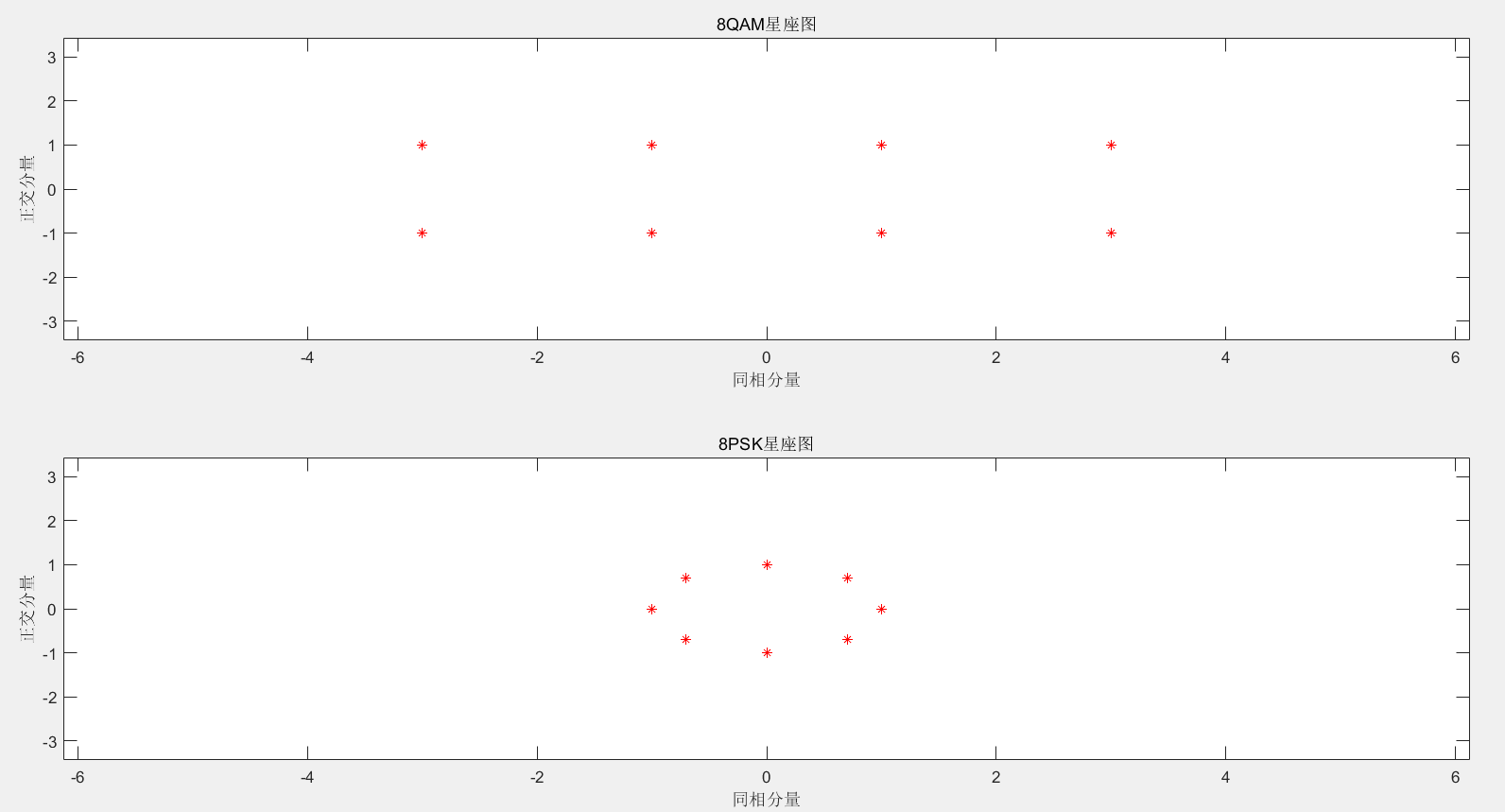
另外一个角度，从上图可以看出，与PSK不同的是：PSK只有相位的信息，而QAM既有相位信息又有幅度信息，可以通过上图（PSK图应该是个圆形）看出。

二、仿真的过程

代码如下（可以改变信噪比ESNO的值，来人为观察误码率，在测试的时候可以把信噪比提高）：

clear all;close all;clc;
n_symbol=1000;                           %%符号个数
T=1;                                     %%表达式中的参数,符号速率（一组载波运载一个符号）
fs=100;  
ts=1/fs;
t=0:ts:T-ts;
fc=1;                                 %%载波频率
c=sqrt(2/T)*exp(j*2*pi*fc*t);         %%载波信号生成两个正交载波
c1=sqrt(2/T)*cos(2*pi*fc*t); 
c2=-sqrt(2/T)*sin(2*pi*fc*t);
M=8;
ESNO=15;                              %%单位dBD   
snr=10.^(ESNO/10);                    %%转换成单位线性值
msg_QAM=randi(M,1,n_symbol);
msgmod_QAM=qammod(msg_QAM-1,M).';     %%qam调制
x=msgmod_QAM*c;
x1=reshape(x.',1,length(msgmod_QAM)*length(c));
s_pow=norm(x1).^2/(n_symbol);                  %%这里是符号的平均功率，而不是每一个采样点
sigma=sqrt(s_pow/(2*snr));                     %%根据线性值的信噪比和信号功率求出噪声功率
x_n_QAM=x1+sigma*randn(1,length(x1));              %%加性噪声后的信号
x_n1_QAM=reshape(x_n_QAM,length(c),length(msgmod_QAM));    %%将合成信号分解一下以便后面的相干计算
r1=(c1*x_n1_QAM).*T/length(c);                     %%相干计算
r2=(c2*x_n1_QAM).*T/length(c);
r=(r1+j*r2)/2;
y1_QAM=qamdemod(r,M)+1;                            %%qam解调 
%想要将原符号来做比较验证误码率，可以为了将数字信号展开做比较
for i=1:n_symbol                    
    msg_x((100*i-99):100*i)=msg_QAM(i);
    y1_x((100*i-99):100*i)=y1_QAM(i);  
end
figure;
subplot(3,2,[1 2]);
plot(msg_x);title(['原信号,信噪比为',num2str(ESNO),'dB；符号数为：',num2str(n_symbol)]);
subplot(3,2,3);
plot(msgmod_QAM,'*r');title('调制信号星座图');
xlabel('同相分量');ylabel('正交分量');
zuobiao=max(real(msgmod_QAM))*1.2;
axis([-zuobiao zuobiao -zuobiao zuobiao]);
subplot(324);
plot(r,'.y');title('经过信道的调制信号星座图');
xlabel('同相分量');ylabel('正交分量');
hold on;
plot(msgmod_QAM,'*r');
axis([-zuobiao zuobiao -zuobiao zuobiao]);
subplot(3,2,[5 6]);
[err,ser]=symerr(msg_QAM,y1_QAM);
plot(y1_x);title(['解调信号，误比特率为：',num2str(ser)]);

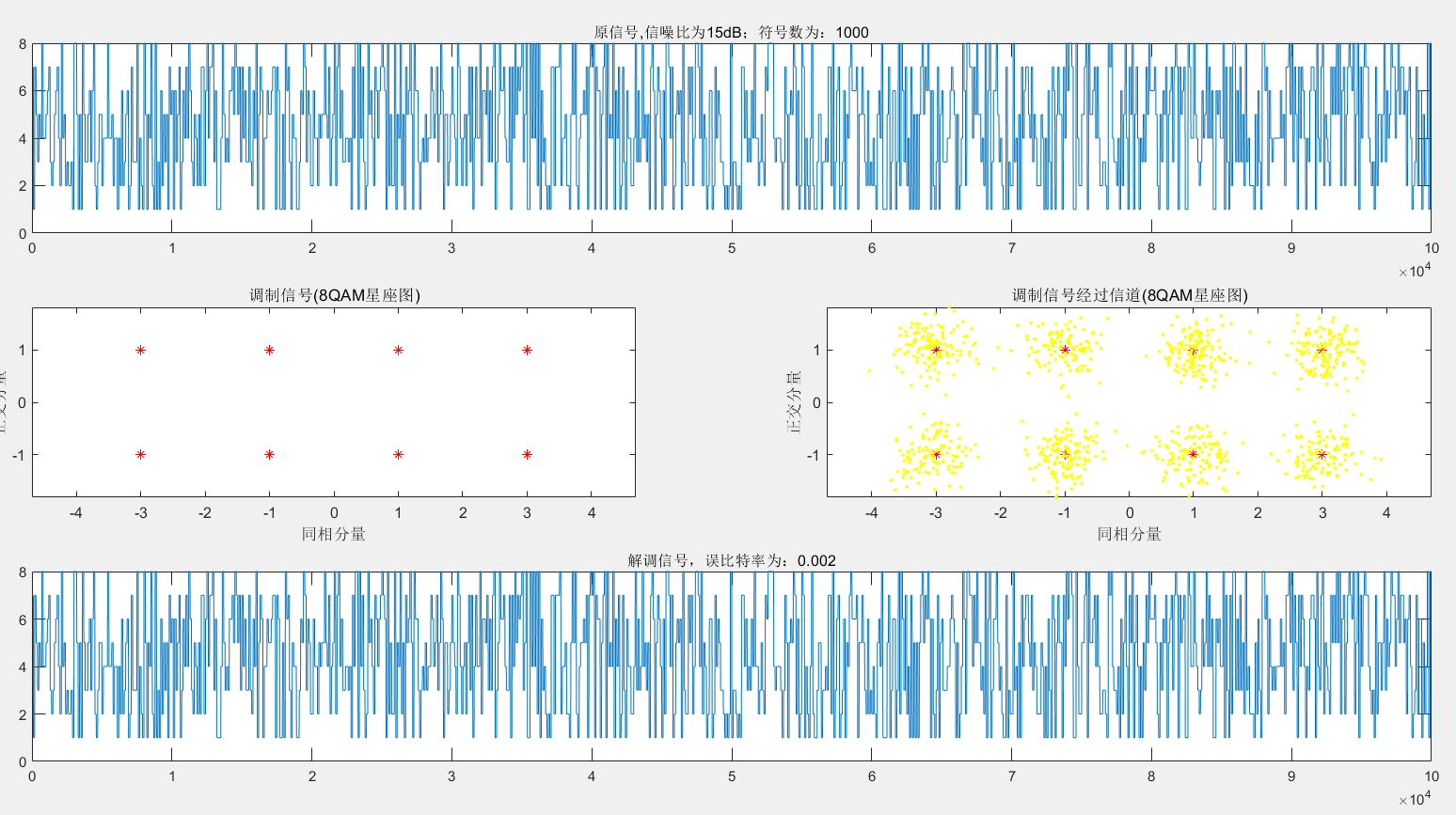
下面三张图片分别是M=4-8-16时候的情况，也可以看出M越大，误码率越大（也是因为间距变小，更容易判错）。当然，还可以比较M相同时，不同信噪比下的误码率，如之前的做法相似。公式如下：

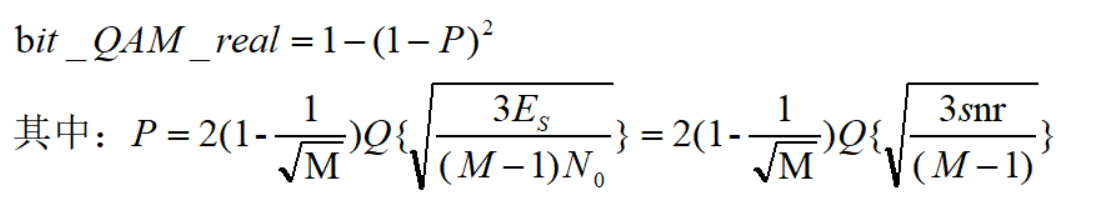
4QAM:

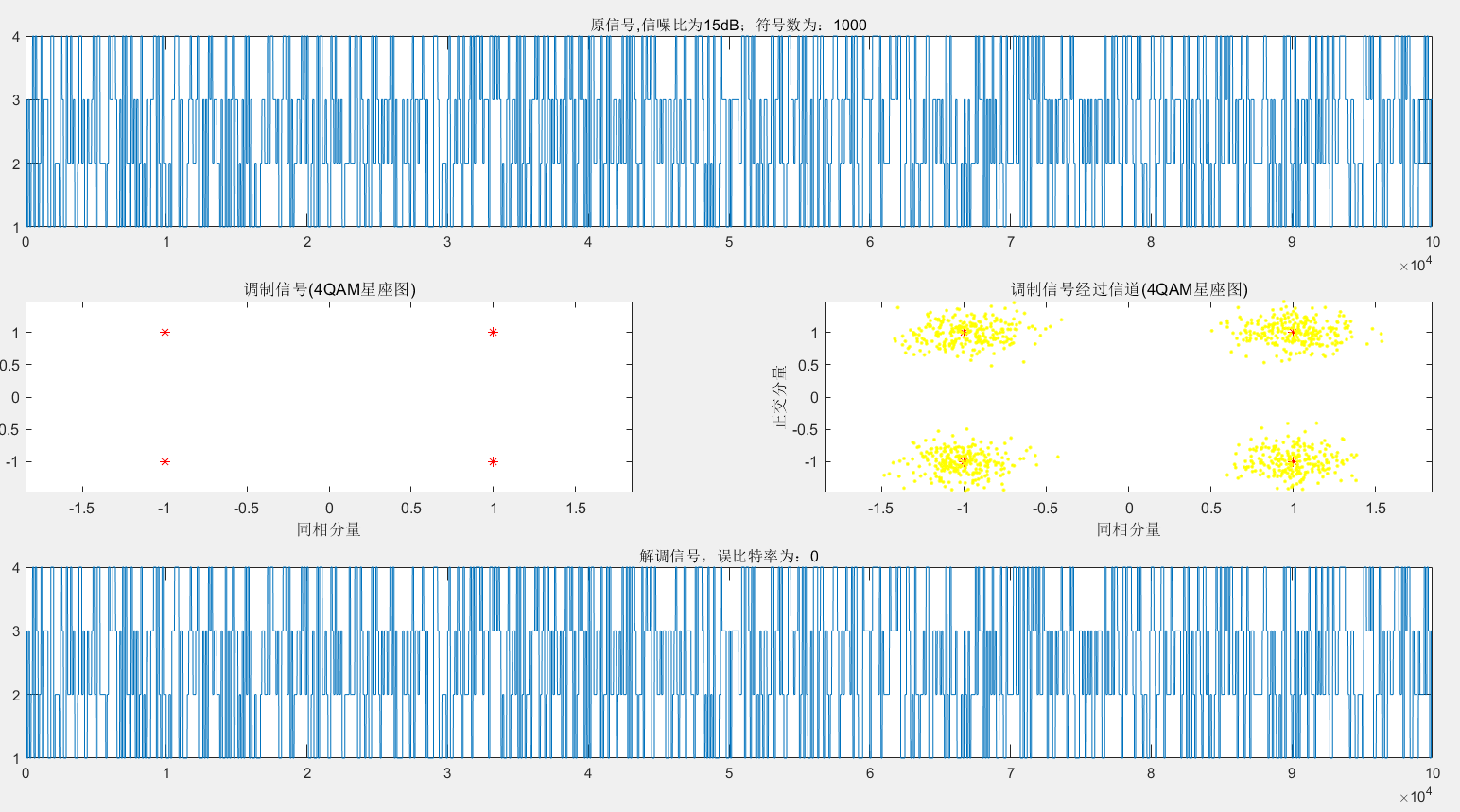
8QAM:

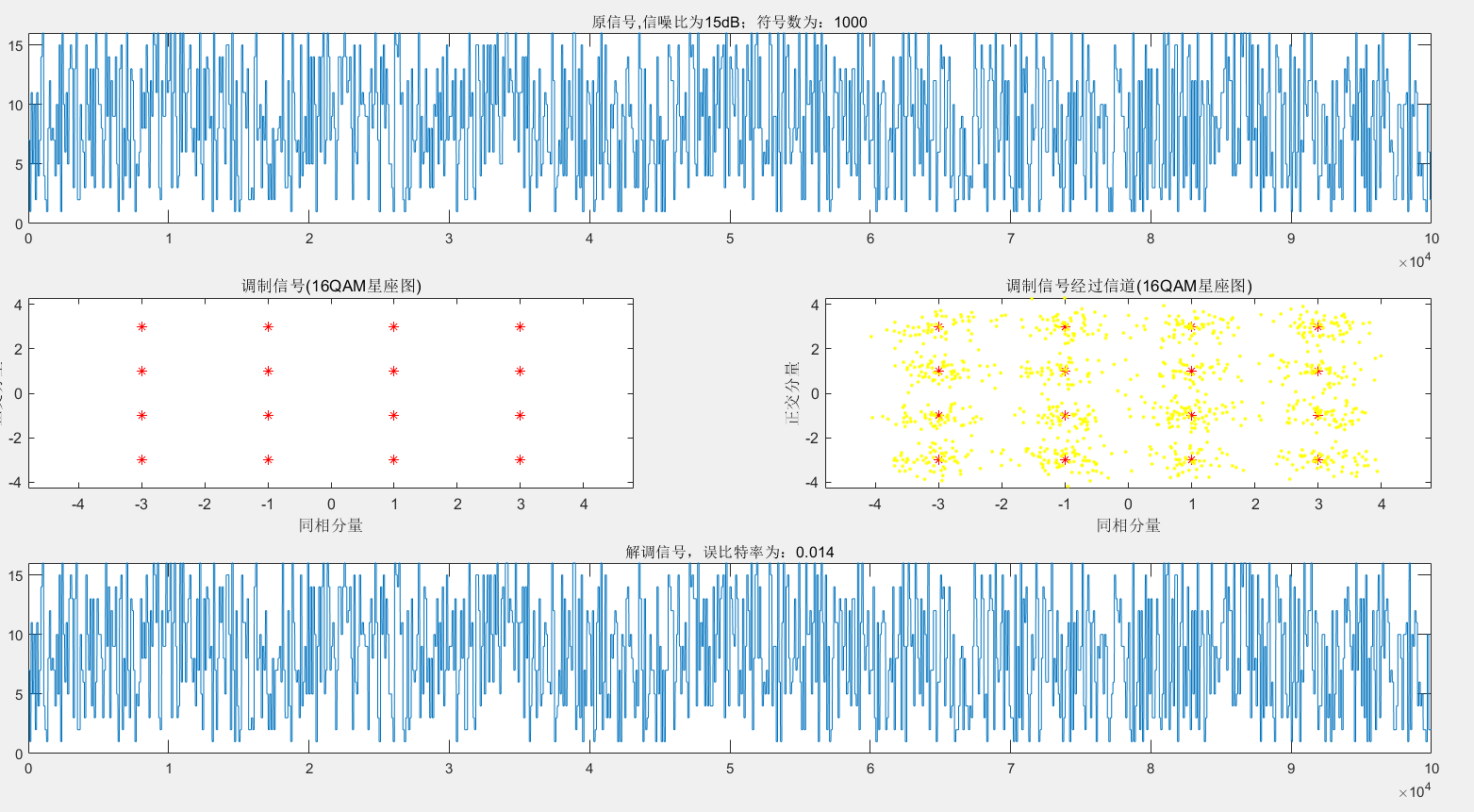
16QAM:

最后

以上就是怕孤单老鼠为你收集整理的正交幅度调制（QAM)前言一、调制和解调的过程二、仿真的过程的全部内容，希望文章能够帮你解决正交幅度调制（QAM)前言一、调制和解调的过程二、仿真的过程所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。