点击上方蓝字设为星标
 本文来源于力扣圈子,作者:小白二号
原文链接:https://leetcode-cn.com/circle/article/7FXJsv/
本文来源于力扣圈子,作者:小白二号
原文链接:https://leetcode-cn.com/circle/article/7FXJsv/

背景
搜索是优化算法题的本源。所有的优化算法题均是在一个有限的搜索空间中,寻找最优解答。注意这里是有限的搜索空间,就算是实数的返回,也会有精度的要求,就算是二分,也会有搜索的上下界。
有些朋友在学习递归,回溯,动态规划,深度优先搜索,广度优先搜索等算法问题时,时常搞不清楚状态对象和状态转移。因此我开这个话题,聊聊搜索中的状态空间,以及高级算法中的思考方式。

搜索通解
假设一个题目的状态为 A,那么这个题目的通解是:
Java 实现
void search() {// 枚举所有的状态 for (A a : all) { collect(a); }}
状态
搜索题中,题目蕴含的每个变量都有一个上下界,而每个变量组合取值形成了状态空间。树的遍历题中,跟到叶子的路径是一个状态,图论题中,源点到所有点的所有路径都是一个状态。状态在理解题意后很容易找到,我随便挑几个题来分别说说状态是什么。
力扣 542.01 矩阵
题目描述
给定一个由 0 和 1 组成的矩阵,找出每个元素到最近的 0 的距离。两个相邻元素间的距离为 1 。
示例 1:
输入:
0 0 00 1 00 0 0输出:
0 0 00 1 00 0 0示例 2:
输入:0 0 00 1 01 1 1输出:
0 0 00 1 01 2 1注意:
给定矩阵的元素个数不超过 10000。
给定矩阵中至少有一个元素是 0。
- 矩阵中的元素只在四个方向上相邻: 上、下、左、右。
解析
这个题比较好找,需要对每个位置找到最近的 0,状态是每个位置到每个 0 的路径。
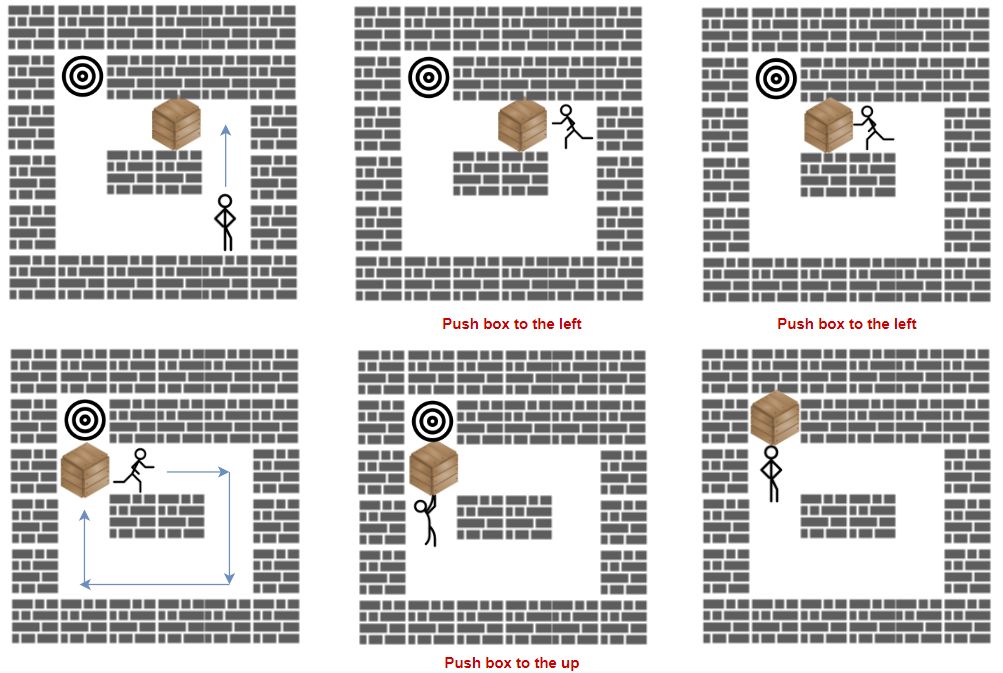
力扣 1263.推箱子
题目描述
「推箱子」是一款风靡全球的益智小游戏,玩家需要将箱子推到仓库中的目标位置。
游戏地图用大小为 n * m 的网格 grid 表示,其中每个元素可以是墙、地板或者是箱子。
现在你将作为玩家参与游戏,按规则将箱子 'B' 移动到目标位置 'T' :
玩家用字符
'S'表示,只要他在地板上,就可以在网格中向上、下、左、右四个方向移动。地板用字符
'.'表示,意味着可以自由行走。墙用字符
'#'表示,意味着障碍物,不能通行。箱子仅有一个,用字符
'B'表示。相应地,网格上有一个目标位置'T'。玩家需要站在箱子旁边,然后沿着箱子的方向进行移动,此时箱子会被移动到相邻的地板单元格。记作一次「推动」。
玩家无法越过箱子。
返回将箱子推到目标位置的最小 推动 次数,如果无法做到,请返回 -1。
示例 1:

示例 2:

示例 3:

示例 4:

提示:
1 <= grid.length <= 201 <= grid[i].length <= 20grid仅包含字符'.','#','S','T', 以及'B'。grid中'S','B'和'T'各只能出现一个。
解析
这个题有两个对象在动,一个是人,一个是箱子,因此每个搜索节点都是四维的。状态是初始人和箱子的位置到箱子落到目标点的路径。
力扣 70 爬楼梯
题目描述
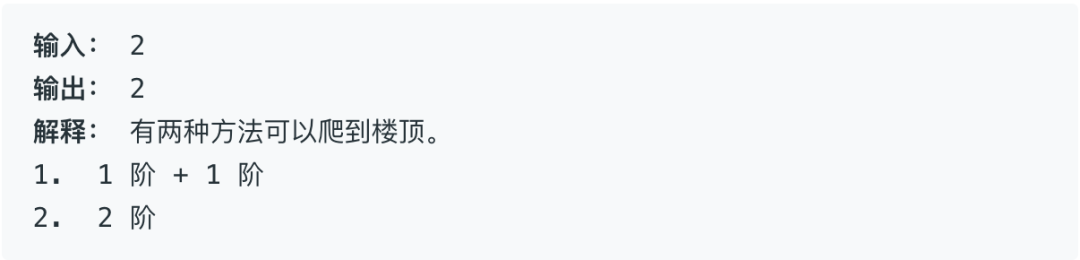
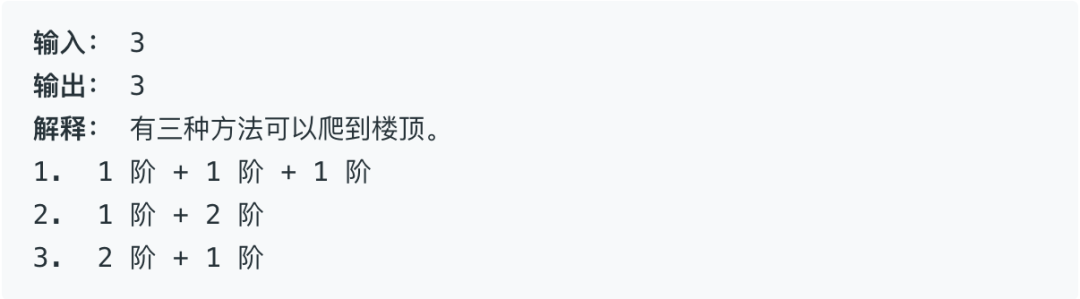
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
示例 1:
示例 2:
解析
从 1 级爬到 n 级的所有每一种情况,比如说,[1,2,1] 是 4 阶楼梯的一种方案。
力扣 322 零钱兑换
题目描述
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
示例 1:

示例 2:
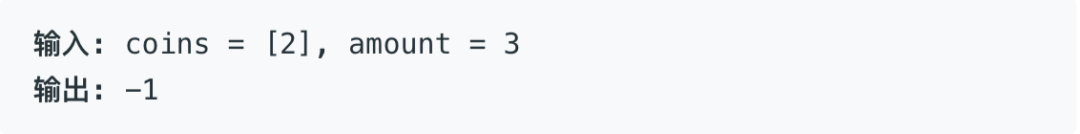
说明:
你可以认为每种硬币的数量是无限的。
解析
每个硬币的参与计算的个数要么是 0(被取),要么是 1(没被取),所以每个硬币的参与计算的个数形成了状态,状态是个 1*n 的数组。
力扣 31 下一个排列
题目描述
实现获取下一个排列的函数,算法需要将给定数字序列重新排列成字典序中下一个更大的排列。
如果不存在下一个更大的排列,则将数字重新排列成最小的排列(即升序排列)。
必须 原地 修改,只允许使用额外常数空间。
以下是一些例子,输入位于左侧列,其相应输出位于右侧列。
1,2,3 → 1,3,23,2,1 → 1,2,31,1,5 → 1,5,1
解析
每个元素有 1-n 的取值范围,所有元素的取值构成了一个状态,状态是个 1*n 的数组。这题的状态是有约束的,所有的取值不能相同。

状态枚举
问题描述
给定一个数组 a[n],枚举所有的 n 维数组 b[n],并且 1
假设 n 等于 2,两个 for 循环搞定,n 等于 3 时,可以三个 for 循环,但是 n 为无限长呢?
递归
void visit(vector<int>& data) {}void dfs(vector<int>& a, vector<int>& b, int index) { if (index == a.size()) { visit(b); return; } for (int i = 1;i <= a[index];i++) { b[index] = i; dfs(a, b, index + 1); }}进制
void visit(vector<int>& data) {}bool next(vector<int>& a, vector<int>& b) { b[i]++; for (int i = 0;i + 1 < a.size();i++) { if (b[i] == a[i]) { b[i] = 0; b[i + 1]++; } else { break; } } if (b[a.size() - 1] == a[a.size() - 1]) { return false; } else { return true; }}void iter(vector<int>& a) { vector<int> b(a.size(), 1); while (next(a, b)) { visit(b); }}
状态前缀树(搜索树)
从上面的枚举过程,dfs 解法中可以看出,我们固定的是前 index 个点,然后继续枚举第 index+1 个点,搜索的过程相当于把状态的相同前缀合并了,枚举每一个前缀,然后从这个前缀出发,继续枚举下一个点。
大部分题,我们枚举到某一个前缀,就可以根据题目的某些特殊的要求,判断这个状态前缀是否成立,达到剪枝的目的。
比如说,枚举排列,就在上面的 dfs 代码中加入了判断状态前缀是否出现了相同数字。
void visit(vector<int>& data) {}void dfs(vector<int>& b, set<int>& picked, int index) { if (index == a.size()) { visit(b); return; } for (int i = 1;i <= b.size();i++) { //只要是已经出现在b中的数,这个状态前缀就没必要接着往下搜 if (picked.find(i) != picked.end()) { continue; } b[index] = i; picked.insert(i); dfs(a, b, index + 1); //回溯,由于把i插入到picked是这个循环块的操作,那么由这个循环负责回收 picked.erase(i); }}
本文作者:小白二号
编辑&版式:霍霍
声明:本文归作者版权所有,如需转载请联系。

点个在看,少个 bug?
最后
以上就是怕孤独信封最近收集整理的关于判断字段是否与枚举相同_算法和数据结构 | 状态枚举(一)的全部内容,更多相关判断字段是否与枚举相同_算法和数据结构内容请搜索靠谱客的其他文章。








发表评论 取消回复