首先，这篇文章是看了各位大神的博客，然后自己把自己的思路总结记录下来，其中有很多图片以及公式，是拷贝自这些大神的博客，在此表示感谢！！！

麦克纳姆轮介绍

首先，上个图，麦克纳姆轮和普通的轮子是不同的，可以看出，麦轮是由轮毂轴和辊子组成的，一般使用的麦轮，轮毂轴和辊子的轴成45°角，不过其实是制作成各种角度的，这里就只介绍常用的麦轮。

安装方式

麦轮一般都是四个一组使用，两个左旋轮，两个右旋轮，具体区别如下图所示

麦轮安装方式，分为X型或者O型，


X型安装方式，会导致旋转力矩很小或者无法旋转(四个轮子安装位置为正方形)的情况发生，因此，本文只针对O型安装方式麦轮来进行分析。

不同行驶状况下的受力情况

以下的图中，小车三角形一侧为车头，另一边为车尾。
所有的实线都是轮子的所受的摩擦力，虚线为摩擦力沿着XY轴的分解力。
图中红色线表示车轮向前旋转，蓝色表示车轮向后旋转。

前后行驶

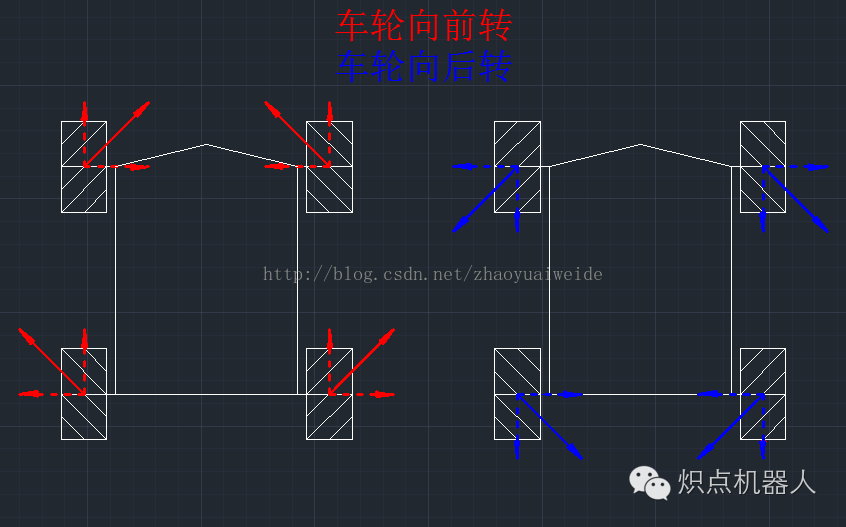
左侧----向前移动
右侧----向后移动

左右平移

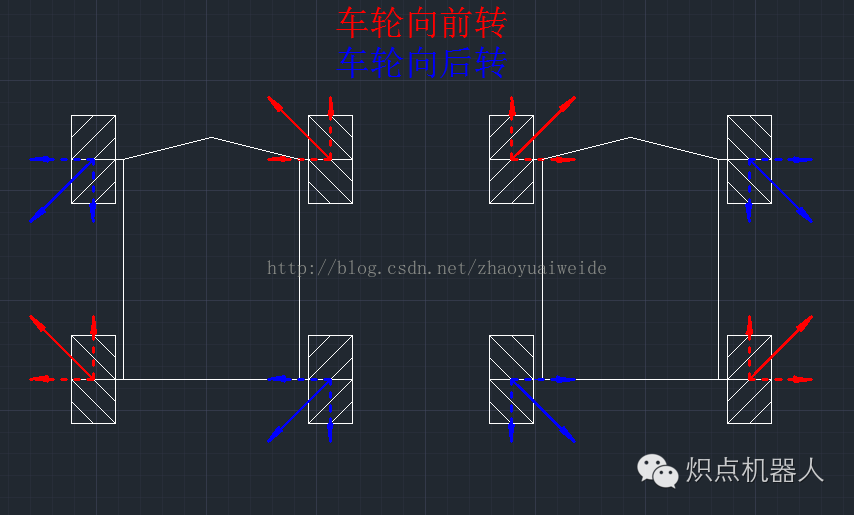
左侧----向左平移
右侧----向右平移

原地旋转

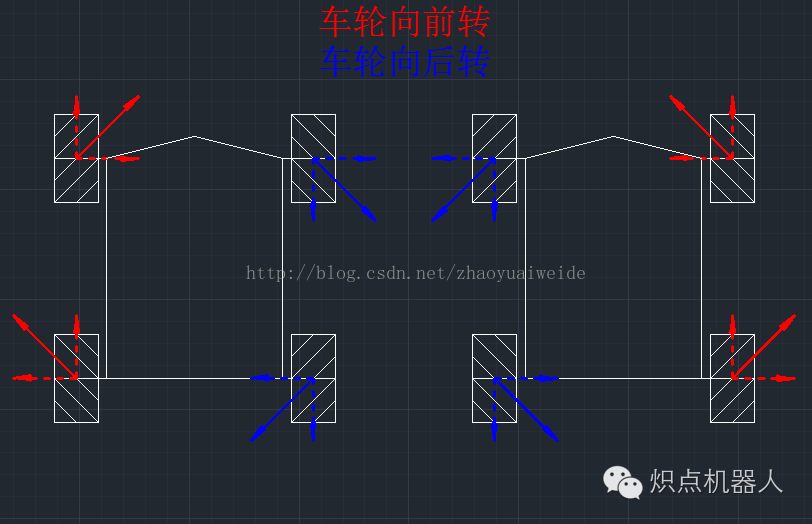
左侧----顺时针旋转
右侧----逆时针旋转

斜方向移动

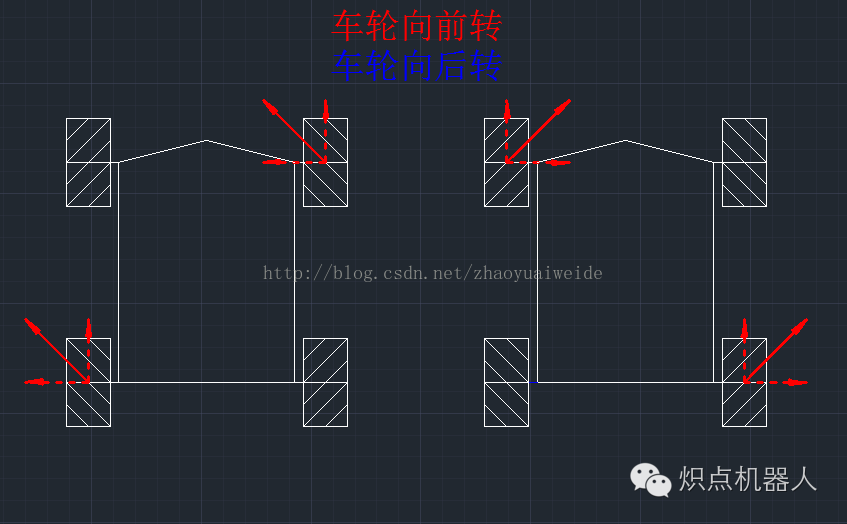
左侧----前方左45°移动
右侧----前方右45°移动

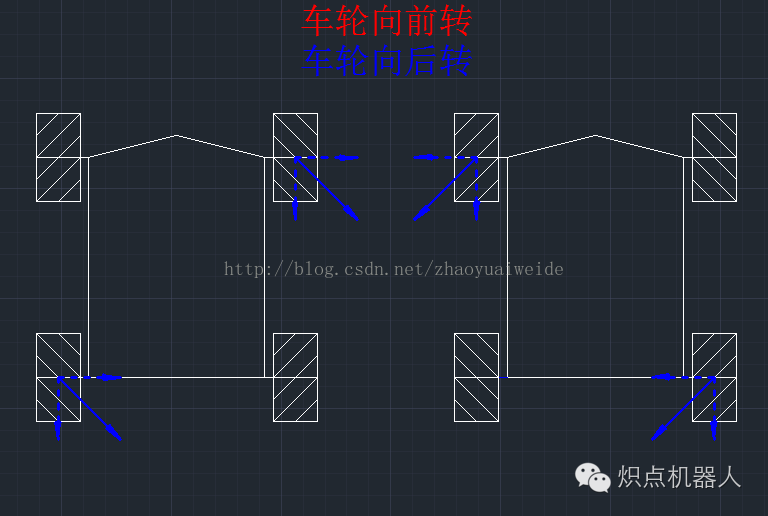
左侧----后方左45°移动
右侧----后方右45°移动
麦轮小车斜着移动的时候，只需要旋转对角线上的两个轮子即可。

麦克纳姆轮正逆运动学模型

以O型的安装方式为例，四个轮子的着地点形成一个矩形，或者正方形，由于加工精度等限制，很难做到四个麦轮安装位置成正方形，并且正方形的安装方式对于车身的控制并没有太大的优势，所以矩形安装方式即可。
AGV小车的运动状态，可以通过三个量来进行描述$v_x,v_y,{\omega }_v$，即是 X 轴方向上的平动，Y 轴方向的平动，以及围绕 Z 轴旋转(逆时针方向为正)。麦轮的四个轮子需要用四个电机独立进行控制，并且四个轮子的速度存在约束，逆运动学方程存在唯一解，正运动方程如果不满足这个约束，则会无解。
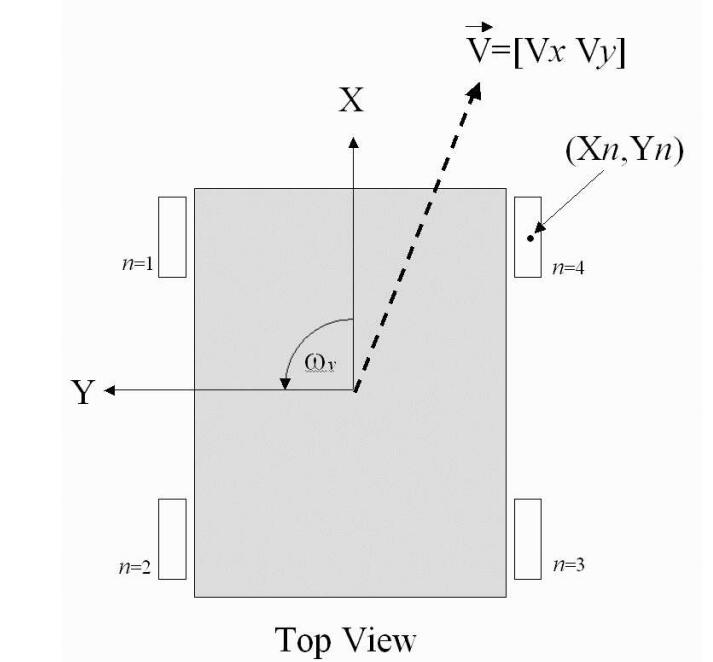
直接上图吧，俯视图如下，四个麦轮平行于X轴的方向安装，从AGV左上角开始逆时针开始，分别为四个麦轮编号为1,2,3,4，r 为轮毂半径，${\theta }_n$ 为麦轮n辊子轴线与X轴线之间的夹角（就是辊子的偏置安装角，大小为45°），$X_n,Y_n$ 为麦轮n的中心点位置

运动学方程

逆运动学(Inverse Kinematic Model)方程，根据期望AGV小车的运动状态求解出四个麦轮的转速以及转向。
正运动学(Forward Kinematic Model)方程，根据四个麦轮的运动状态来预估小车整体的运动状态。
这里介绍一种最简单的计算方式，即将三个正交的底盘运动方向$v_x,v_y,{\omega }_v$进行线性叠加的方式。

因为，底盘安装方式是O型安装

X轴方向运动

AGV向前运动时，只需要四个电机以轮毂轴心为圆心，向X轴正方向旋转麦轮，
向后运动时，只需要四个电机以轮毂轴心为圆心，向X轴负方向旋转麦轮，
此时，底盘期望速度只有X轴方向的速度，$\overrightarrow{V}$是小车的状态向量
$$\overrightarrow{V}=\left[\begin{array}{c}{v}_x,0,0\end{array}\right]$$
可以得到此时的四个麦轮的期望转速，$k_x$为系数，需根据实际情况整定
$$\{\begin{array}{l}{v}_1=v_x\ast k_x\\ v_2=v_x\ast k_x\\ v_3=v_x\ast k_x\\ v_4=v_x\ast k_x\end{array}$$

Y轴方向运动

AGV小车需要沿着Y轴正方向运动时，1、 3号轮沿着轮毂轴向着X轴负方向旋转，2 、4号轮沿着轮毂轴向着X轴正方向旋转；小车需要沿着Y轴负方向运动时，1、 3号轮和2 、4号轮的旋转方向相反。

此时，底盘期望速度只有Y轴方向的速度，小车的状态向量为
$$\overrightarrow{V}=\left[\begin{array}{c}0,v_y,0\end{array}\right]$$
可以得到此时的四个麦轮的期望转速，$k_x$为系数，需根据实际情况整定
$$\{\begin{array}{l}{v}_1=-v_y\ast k_y\\ v_2=v_y\ast k_y\\ v_3=-v_y\ast k_y\\ v_4=v_y\ast k_y\end{array}$$

Z轴旋转

首先，Z轴是XY交点指向小车顶部为正方向，需要小车逆时针旋转的话，1、 2轮向X轴正方向旋转，3、 4轮向X轴负方向旋转；顺时针旋转的话，1、 2轮和3、 4轮的旋转方向相反。
小车此时的状态向量为
$$\overrightarrow{V}=\left[\begin{array}{c}0,0,{\omega }_v\end{array}\right]$$
四个麦轮的转速为
$$\{\begin{array}{l}{v}_1=-{\omega }_v\ast (a+b)\\ v_2=-{\omega }_v\ast (a+b)\\ v_3={\omega }_v\ast (a+b)\\ v_4={\omega }_v\ast (a+b)\end{array}$$
式中，a为任意一个麦轮到X轴的距离，b为任意一个麦轮到Y轴的距离。

合成速度

综合上述，可以有AGV小车的状态向量为
$$\overrightarrow{V}=\left[\begin{array}{c}{v}_x,v_y,{\omega }_v\end{array}\right]$$
对应的麦轮转速为

$$\{\begin{array}{l}{v}_1=v_x\ast k_x-v_y\ast k_y-{\omega }_v\ast (a+b)\\ v_2=v_x\ast k_x+v_y\ast k_y-{\omega }_v\ast (a+b)\\ v_3=v_x\ast k_x-v_y\ast k_y+{\omega }_v\ast (a+b)\\ v_4=v_x\ast k_x+v_y\ast k_y+{\omega }_v\ast (a+b)\end{array}$$

最后，单单做好运动模型的分解是不够的，实际控制过程中，需要电机快速的响应到期望的转速，这样就必须要求对每个电机加上一层PID控制，当然其他的控制也可以，保证电机响应迅速就可以。

最后

以上就是儒雅耳机为你收集整理的AGV-麦克纳姆轮小车控制总结麦克纳姆轮介绍安装方式不同行驶状况下的受力情况麦克纳姆轮正逆运动学模型的全部内容，希望文章能够帮你解决AGV-麦克纳姆轮小车控制总结麦克纳姆轮介绍安装方式不同行驶状况下的受力情况麦克纳姆轮正逆运动学模型所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。