目录
- 1. 分布的形式化
- 参考资料
度娘百科:
耿贝尔分布是根据极值定理导出,由费雪(R·A·Fisher ) 和蒂培特(L·H·C·Tippe -t t) 于1928 年发现各个样本的最大值分布将趋于三种极限形式种的一种,具体由型式参数K确定,当K=0的时候也就是耿贝尔分布,水文方面主要用第I 型渐近极值分布,是耿贝尔在1941年将此分布应用于洪水频率分析工作,所以也称Fisher一Tippe 优工型分布。
耿贝尔分布主要是适用于对海洋、水文、气象,来计算不同重现期的极端高(低)潮位。 [1] 海洋的年最高水位可以认为是由天文潮和许多随机因子的影响形成的。因此,它可以用耿贝尔极值I型分布函数进行拟合。
Wikipedia:
在概率论和统计学中,Gumbel 分布(广义极值分布类型-I)用于模拟各种分布的多个样本的最大值(或最小值)的分布。如果存在过去十年的最大值列表,则该分布可用于表示特定年份中河流的最大水平的分布。
它可用于预测极端地震,洪水或其他自然灾害发生的可能性。Gumbel 分布代表最大值分布的潜在适用性与极值理论有关,表示如果基础样本数据的分布是正常或指数类型,它可能是有用的。本文的其余部分引用 Gumbel 分布来模拟最大值的分布。要对最小值建模,请使用原始值的负值。
Gumbel 分布是广义极值分布(也称为 Fisher-Tippett 分布)的特例。它也被称为 log- Weibull 分布和双指数分布(或者有时用于表示拉普拉斯分布的术语)。它与 Gompertz 分布有关:当其密度首先反映原点然后限制为正半线时,获得 Gompertz 函数。
在多项 logit 模型的潜在变量公式中- 在离散选择理论中常见- 潜在变量的误差遵循 Gumbel 分布。这很有用,因为两个 Gumbel 分布的随机变量的差异具有逻辑分布。
Gumbel分布以Emil Julius Gumbel(1891-1966)命名,基于他描述分布的原始论文。[1] [2]
1. 分布的形式化
物理意义
Gumbel 分布(耿贝尔分布)是一种极值型分布。
举例而言,假设每次测量心率值为一个随机变量(服从某种指数族分布,如正态分布),每天测量10次心率并取最大的一个心率值作为当天的心率测量值。
显然,每天纪录的心率值也是一个随机变量,并且它的概率分布即为 Gumbel 分布。
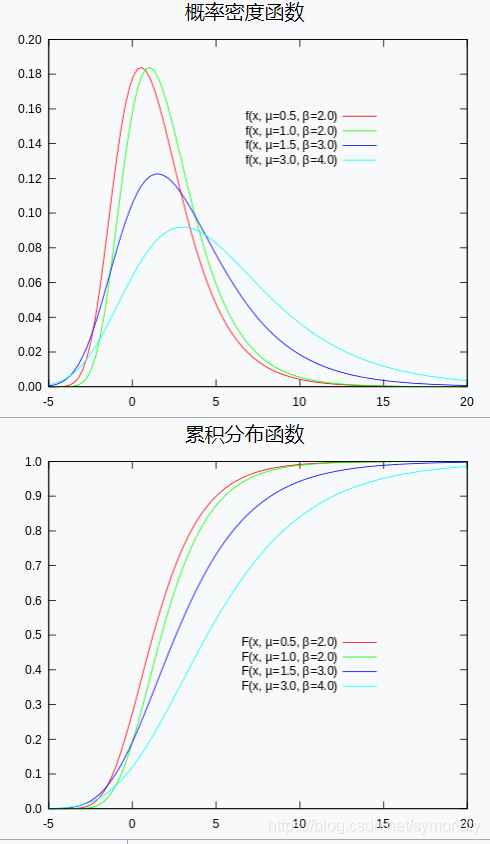
概率密度函数(PDF)
Gumbel 分布的 PDF 如下:
f
(
x
;
μ
,
β
)
=
e
−
z
−
e
−
z
,
z
=
x
−
μ
β
f(x;mu,beta)=e^{-z-e^{-z}},z=frac{x-mu}{beta}
f(x;μ,β)=e−z−e−z,z=βx−μ
公式中,
μ
mu
μ是位置系数(Gumbel 分布的众数是
μ
mu
μ),
β
beta
β是尺度系数(Gumbel分布的方差是
π
2
6
β
frac{pi^2}{6}beta
6π2β
def gumbel_pdf(x, mu=0, beta=1):
z = (x - mu) / beta
return np.exp(-z - np.exp(-z)) / beta
print(gumbel_pdf(0.5, 0.5, 2))
累计密度函数(CDF)
相应的,gumbel 分布的 CDF 的公式如下:
f
(
x
;
μ
,
β
)
=
e
−
e
−
x
−
μ
β
f(x;mu,beta)=e^{-e^{-frac{x-mu}{beta}}}
f(x;μ,β)=e−e−βx−μ
def gumbel_cdf(x, mu=0, beta=1):
z = (x - mu) / beta
return np.exp(-np.exp(-z))
print(gumbel_cdf(5, 0.5, 2))
参考资料
[1] Laboratory for Intelligent Probabilistic Systems;
[2] 10.耿贝尔分布(Gumbel distribution) 2018.7.16;
最后
以上就是正直小蝴蝶最近收集整理的关于Gumbel 分布介绍(耿贝尔分布)1. 分布的形式化参考资料的全部内容,更多相关Gumbel内容请搜索靠谱客的其他文章。








发表评论 取消回复