广义帕累托分布

也许你没有听说过广义帕累托分布，但是你一定听说过二八定律，即世界上20%的人掌握着80%的财富，它就来源于广义帕累托分布。广义帕累托是极值分析中一种极其重要的分布，用于估计较大值出现的规律。

目前接触到的项目需要对较大的值出现概率进行估计，并进行极值外推，预测未来极值出现的规律。

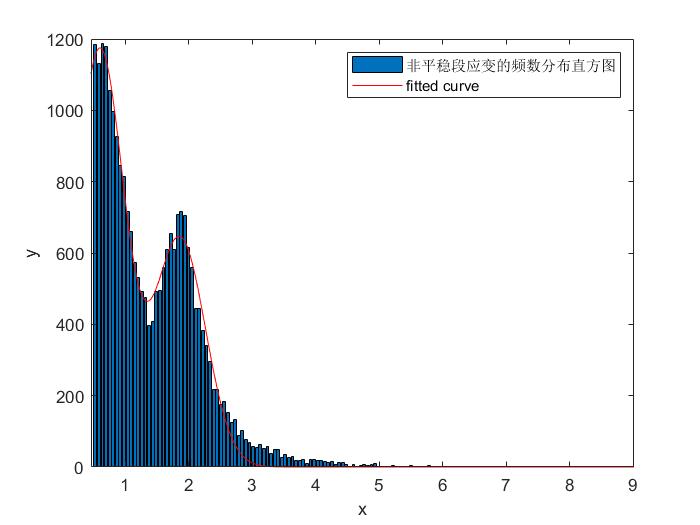
可以看到双峰分布对尾部数据拟合并不好

由于我们主要关心的是尾部数据，结果偏偏尾部数据估计的结果还不好，所以我们考虑尝试使用广义帕累托分布

使用matlab进行广义帕累托分布参数估计

究竟哪一部分的值才作为尾部数据，来进行帕累托分布呢？

这时候就要定一个阈值u，超出这个阈值的数据点才作为拟合的对象，并且将其减去阈值，然后得到的值才是我们要去拟合的数据点。

%% 读取数据
load('yb.mat');
yb1 = yb;
czyb=yb1(yb1>u)-u;  %准备拟合的数据点
ybs=length(czyb);   %超出阈值的数据点个数
%% 参数估计(最大似然估计）
paramEsts = gpfit(czyb);
kHat = paramEsts(1);       %形状系数
sigmaHat = paramEsts(2);   %尺度系数

这里的拟合非常简单，其实我之前不知道matlab中有这个的内置包，我就自己写了最小二乘法，结果是一样的，但是运行速度较慢。参数估计很简单就完成了。

图像检查拟合效果

figure(1)
bins = 0:0.1:6;
h = bar(bins,histc(czyb,bins)/(ybs*0.1),'histc');
h.FaceColor = [.9 .9 .9];
ygrid = linspace(0,1.1*max(czyb),1000);
line(ygrid,gppdf(ygrid,kHat,sigmaHat),'linewidth',2); %积分只有0.1，没有1
xlabel('超出量');
ylabel('概率分布');
legend('频率分布直方图','GPD拟合');

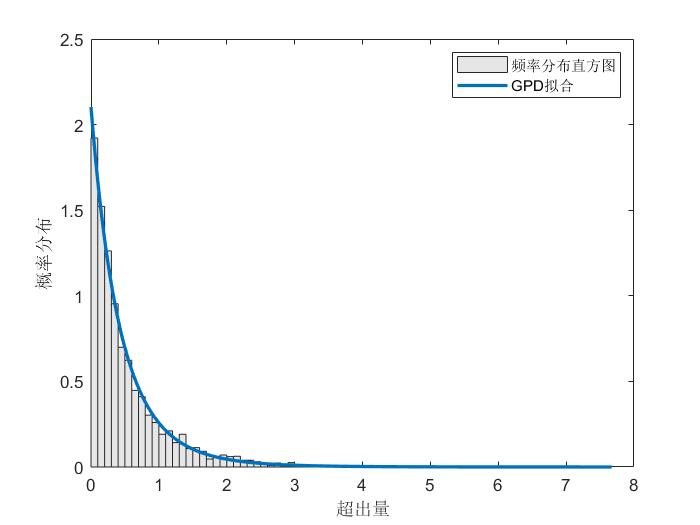
这样可以看出CDF、PDF的拟合都是非常好的

有一点要注意：就是

histc(czyb,bins)/(ybs*0.1)

代码中算频率分布直方图的时候为啥分母乘了0.1，这是因为这个内置的包，或者说我们用最小二乘法计算的参数，得到的帕累托分布，定义域积分出来是1的。如果分母不乘0.1，频率分布直方图的“积分值”合计为0.1，此时拟合效果看起来就非常差，所以要让频率分布直方图的“积分”也是1。

极值外推

其核心就是下面2.27这个公式，由此可以计算任意时长的极值分布。

不同时长的极值分布如图所示：

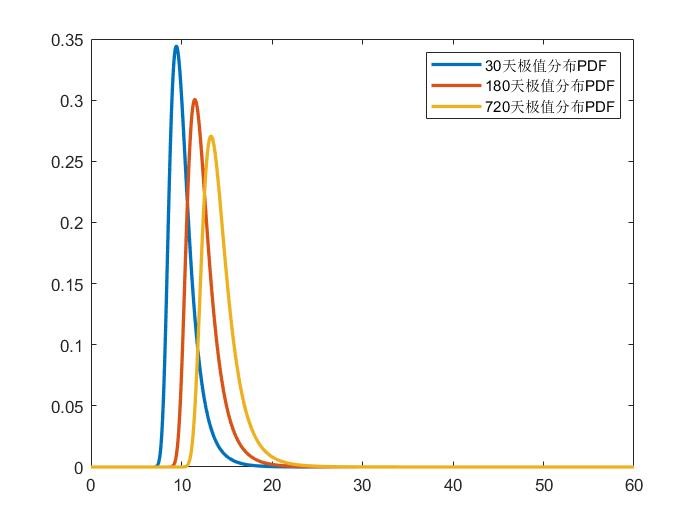
此处可以参考：

还有一些问题

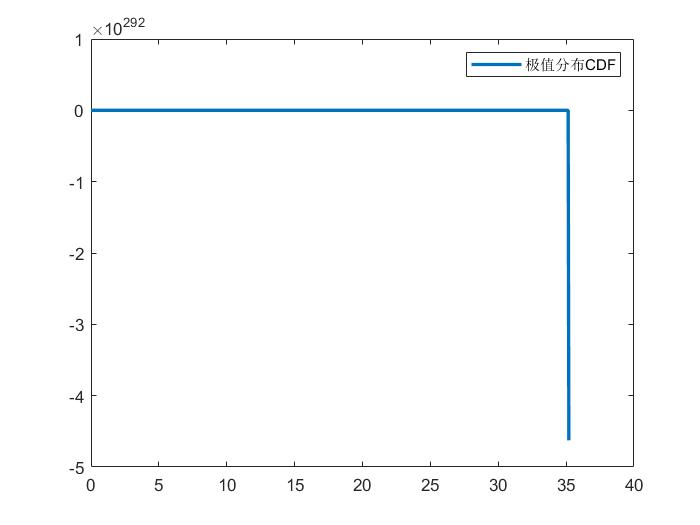
极值外推有时候会有问题

极值分布的PDF、CDF有时不正常

阈值选取的艺术

阈值选小了，和之前的拟合没啥区别，效果不好
阈值选大了，剩余的样本点太少了，效果不好

怎么找到最合适的进行广义帕累托分布的阈值呢？

欢迎大家一起交流。

最后

以上就是干净太阳为你收集整理的MATLAB数据处理（2）——广义帕累托分布和极值外推广义帕累托分布的全部内容，希望文章能够帮你解决MATLAB数据处理（2）——广义帕累托分布和极值外推广义帕累托分布所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。