常见分布总结-高斯分布、伯努利分布、泊松分布、几何分布、beta分布

概率分布
概率分布是指用于表述随机变量取值的概率规律，包括连续分布和离散分布。
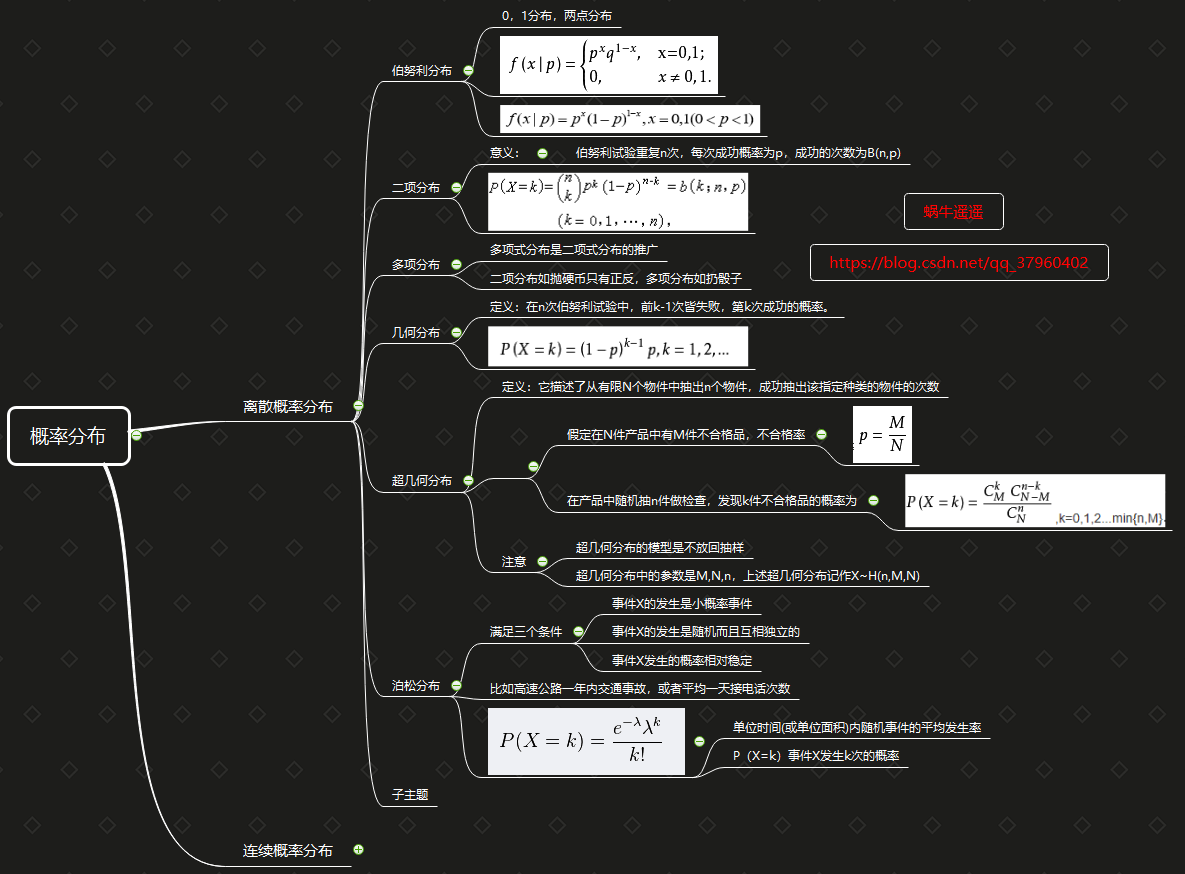
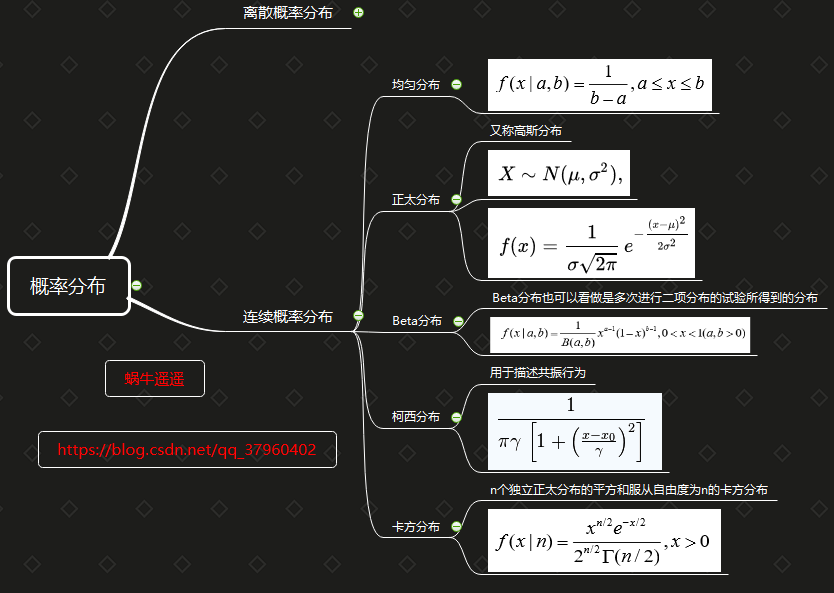
下面作了这些概率分布的一个思维导图。

概率分布

1、离散概率分布

1.1、两点分布

意义：指的是一次实验中有两个事件，成功或者失败，出现的概率记为p，1-p。
分布律：

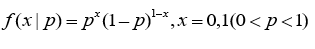
数字特征：

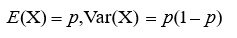
举例：比如一个口袋中有十个球，其中红球3个，白球7个，问从中取到红球的概率？
f=0.3¹ ×0.7⁰=0.3

2.2、 二项分布

意义：两点分布独立重复n次，则实验成功的次数服从一个参数为(n,p)的二项分布
分布律：

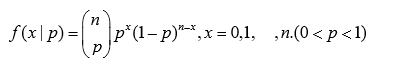
或者

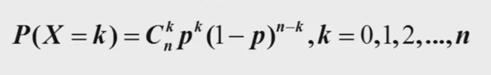
数字特征：

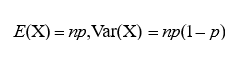
举例：比如一个口袋中有100个球，其中红球30个，白球70个，重复有放回地取30次，其中有10次取到红球的概率？
f=C₃₀¹⁰ (0.3)¹⁰*(0.7)²⁰

1.3、几何分布

其中一种定义为：在n次伯努利试验中，试验k次才得到第一次成功的机率。详细的说是：前k-1次皆失败，第k次成功的概率。
分布律：

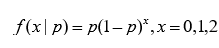
数字特征：

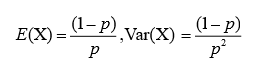
举例：比如一个口袋中有100个球，其中红球30个，白球70个，第10次取到红球的概率？
f=0.3×0.7⁹

1.4、超几何分布

定义：它描述了从有限N个物件中抽出n个物件，成功抽出该指定种类的物件的次数
在产品质量的不放回抽检中，若N件产品中有M件次品，抽检n件时所得次品数X=k，则

数字特征：

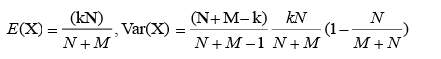
1.5、泊松分布

泊松分布是经济生活中一种非常重要的分布形式，在生活中有很多应用，如：物料订单的规划，道路交通信号灯的设计，生产计划的安排，海港发货船期的调度。
分布律：

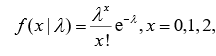
数字特征

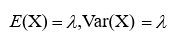
例子：
1、通过某路口的每辆汽车发生事故的概率为p=0.0001，假设在某路段时间内有1000辆汽车通过此路口，则求此时间段内发生交通事故次数X的概率分布。

通过路口的1000辆车是否发生交通事故，可以看成n=1000次伯努利试验，所以X服从二项分布，由于n=1000很大，p=0.0001很小，且np=0.1，所以X服从泊松分布，

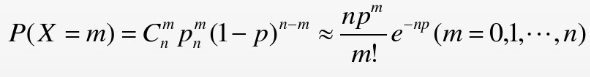
此段时间内发生两次交通事故为：

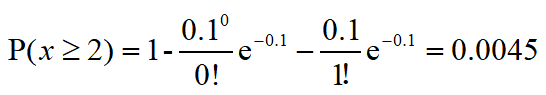
2、连续概率分布

2.1、均匀分布

在概率论和统计学中，均匀分布也叫矩形分布，它是对称概率分布，在相同长度间隔的分布概率是等可能的。 均匀分布由两个参数a和b定义，它们是数轴上的最小值和最大值，通常缩写为U（a，b）
密度函数：

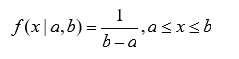
数字特征：

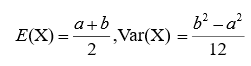
例：设电阻值R是一个随机变量，均匀分布在900ΩΩ~ 1100ΩΩ.求R概率密度及R落在950ΩΩ~1050ΩΩ的概率。
解：R的概率密度为

因此：

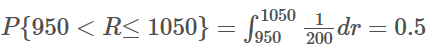
2.2、正太分布

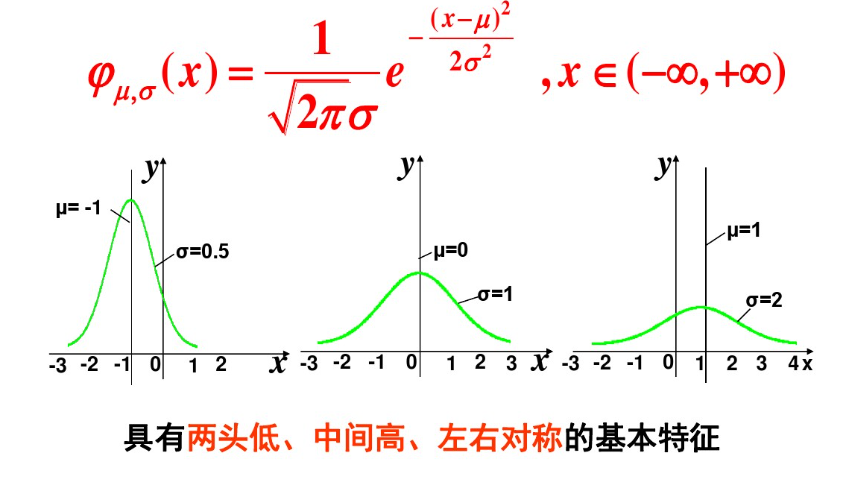
正态分布（Normal distribution），也称“常态分布”，又名高斯分布。
若随机变量X服从一个数学期望为μ、方差为σ²的正态分布，记为N(μ， σ²)。
其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。
当μ = 0,σ = 1时的正态分布是标准正态分布。
密度函数：

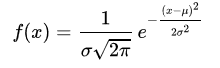
数字特征

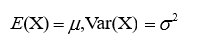
正太曲线的性质：

2.3、beta分布

贝塔分布（Beta Distribution) 是一个作为伯努利分布和二项式分布的共轭先验分布的密度函数。
在概率论中，贝塔分布，也称Β分布，是指一组定义在(0,1) 区间的连续概率分布。

我们先来举个例子，一个袋子里面有很多球，我们不知道球的个数只知道球的颜色（红，白），我们现在从中取出一个球（二次实验），根据先验经验我们猜测红白概率为（0.5，0.5），服从两点分布。那么我们开始有放回地从中抽取100次（多次二项试验），得到红球为70次，黄球为30次，这时候我们又重新猜测红白概率（0.7，0.3）。那么如果我们再将上面试验做150次，即重复150次的多次二次实验，最后得到红白概率为{0.7,0.3}这样概率为多少？这就是beta分布。

函数密度：

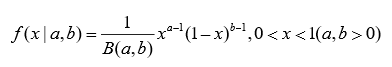
数字特征：

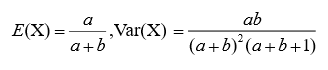
2.4、柯西分布

柯西分布主要应用于物理中，它是描述受迫共振的微分方程的解。在光谱学中，它用来描述被共振或者其他机制加宽的谱线形状。
密度函数：

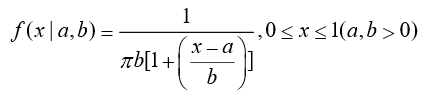
数字特征：均值和方差不存在

2.5、卡方分布

若n个相互独立的随机变量ξ₁，ξ₂，…,ξn ，均服从标准正态分布（也称独立同分布于标准正态分布），则这n个服从标准正态分布的随机变量的平方和构成一新的随机变量，其分布规律称为卡方分布

密度函数：

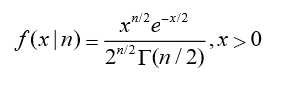
数字特征：

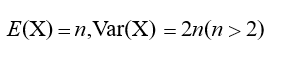
3、参考资料

https://wenku.baidu.com/view/142ccef848d7c1c708a145e3.html
https://wenku.baidu.com/view/8133c0056edb6f1aff001f1c.html
https://www.cnblogs.com/171207xiaohutu/p/9341681.html
https://wenku.baidu.com/view/2b4c13730242a8956bece4e9.html

最后

以上就是过时滑板为你收集整理的常见分布总结-高斯分布、伯努利分布、泊松分布、几何分布、beta分布的全部内容，希望文章能够帮你解决常见分布总结-高斯分布、伯努利分布、泊松分布、几何分布、beta分布所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。