t-SNE原理简述及matlab实现

目录

简介

SNE

SNE优化及困难所在

t-SNE

实验结果

代码链接

使用说明

简介

t-SNE是高维数据可视化的工具，是SNE(Hinton and Roweis在2002年提出)的变体，比SNE更容易优化，通过减弱数据点向中心拥挤的趋势来获取更好的可视化效果。

首先介绍SNE

SNE

SNE将数据点之间的欧拉距离转化为条件概率，这一点很值得借鉴，看问题的角度很重要。将数据点xi作为参考点，求xj到xi的距离，将xi认为是高斯分布的中心，deltai是标准差。则其余数据点到中心的距离被看做是分布概率，两者离得越近，概率越大，离得越远，概率越小。这就把距离近的点的重要性给提上来了。至于标准差怎么求，稍后再说。

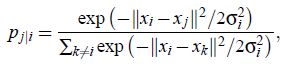
数据可视化一般将数据降维到低维空间，比如2D 3D空间。假设降维后数据点的高斯分布的方差为1/sqrt(2)，则数据点yj与yi的相似度，也就是条件概率为：

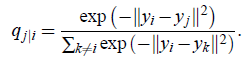
理想状态是，和完全相同。然而这一般是很难做到的，那么我们设置一个损失函数，衡量两个分布的相似性，最先想到的就是KL散度(Kullback-Leibler divergences)：

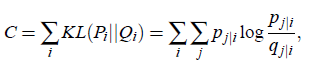
这里用到的就是信息熵的概念，我们假设和相同，那么Cji=0,因为log1=0。如果和差异很大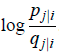，要么是大的正数要么是小的负数，总之与0的偏差很大。这样，利用优化算法来最小化C的值。因为KL不是对称的，也就是说，使用距离很远的点（降维后的空间，即很小）来表示距离很近的点（原数据空间，很大）将造成很大的损失（例如，0.8*log(0.8/0.02)=1.28)，然而使用距离很近的点（降维后的空间，即很大）来表示距离很远的点（原数据空间，很小）造成的损失却很小（例如，0.02*log(0.02/0.8)=-0.03)，这个小的损失就源于降维后的空间的概率密度（也就是0.02）。KL损失函数这样的特性，就使得SNE具有保留原数据空间局部结构的特性（什么意思呢？意思就是，如果你用两个很近的点来表示原来距离很远的点，这样的损失很大，那么降维后的分布就倾向于用距离很的点来表示原来就很近的点，用很远的点来表示原来就很远的点，当然，用很近的点表示原来很远的点的损失也不大，但是多少也会有。哪儿的损失大，最优化时就更关注哪儿，因此，SNE就更关注于原数据的局部结构。其实这里的逻辑是有问题的，它带来的后果是，不同类之间的距离也会越来越近，因为只要用很近的点来表示无论远近的点，损失都很小！这也是t-SNE要解决的问题之一。）

问题是，怎么确定？也就是，我们将欧拉距离转化为高斯条件概率的标准差？具体我也没看懂，好像是用了二进搜索法：

是bit表示的Pi的香农熵，Pi就是以xi为数据中心点时的概率密度函数。

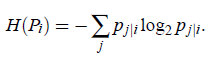
这个困惑度可以认为是有效近邻点的个数，典型值是5-50。

SNE优化及困难所在

损失函数C的优化使用梯度下降，梯度可以表示为：

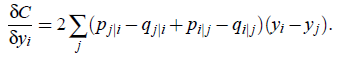
其中，是两个空间中对应概率密度的差，很简单直接，然后乘以降维后空间的两个点的残差，也就是梯度方向。

最优解就是降维后的数据点yi，优化开始时这些点初始化为各向同性的高斯随机数，方差很小，均值为0。为了加快优化并防止陷入局部最优解，使用带动量的梯度下降，也就是说，当前梯度加上之前所有梯度的指数衰减，可以想象指数曲线或者是卷积和之类的，为什么是所有梯度的指数衰减？因为这一项，是递归的，因此包含了最初的梯度，但是由于3-sigma，一般经过几次迭代后，梯度的影响就减少到了可以忽略的程度，可以简单看做是有限支撑的。

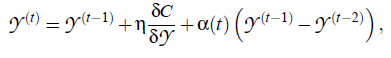
最后的就是我们需要的解，也就是降维后的数据分布。是学习率，是动量。刚开始优化的时候，需要加一些白噪声去防止陷入局部最优，然后逐渐减少白噪声的方差。

如果方差在表示空间全局结构形成的关键点上变化很慢时，SNE趋向于找到一个全局组织更好的解。然而这个最后的解对高斯白噪声的方差的初始值和衰减率很敏感，并且优化时学习率和动量的选择对解也有影响，因此，在一个数据集上多次运行优化以找到合适的参数值是很常见的。

SNE比允许凸优化的方法要差，寻找一种不需要额外计算时间和模拟退火引入的参数选择就能获得良好结果的优化方法是很有用的。

这也是t-SNE的必要性。

t-SNE

t-SNE的主要贡献在损失函数，（1）使用对称版的损失函数，具有更简单的梯度，Cook 等人2007年引入（2）使用Student-t分布代替高斯分布简化计算降维空间里两个点之间的相似度。t-SNE使用重拖尾分布来环节低维空间拥挤和SNE优化困难的问题。

t-SNE首先定义了对称的概率分布，并不是简单的把所有高斯方差变成同一个数，而是把SNE中的概率对儿的和加权：

这样做，每一个xi都能为损失函数做较大贡献。

而低纬度使用一自由度的t分布（其实就是柯西分布）：

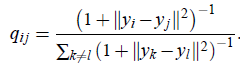
高斯曲线和柯西曲线最大区别就是拖尾，高斯衰减的快，柯西衰减慢，称为重拖尾。

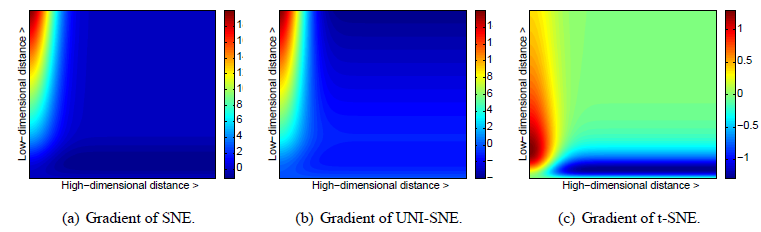
这个图展示的是，高维数据点对儿和低维数据点对儿之间的距离大小与对应梯度的关系，从a和b中可以看出，t-SNE不倾向于用两个近的点表示两个不相似的点，然而这种不倾向并没有太强烈。总之，（1）t-SNE通过大的数据对儿距离的均值来建模不相似的两个点，（2）通过小的距离建模小的数据对儿。另外，使用t分布也使得梯度计算更简单：

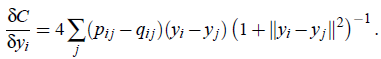
汇总起来：

动量，学习率初始为100，然后自适应的更新。

实验结果

将手写字的图像数据（32*32维）降维成2维。

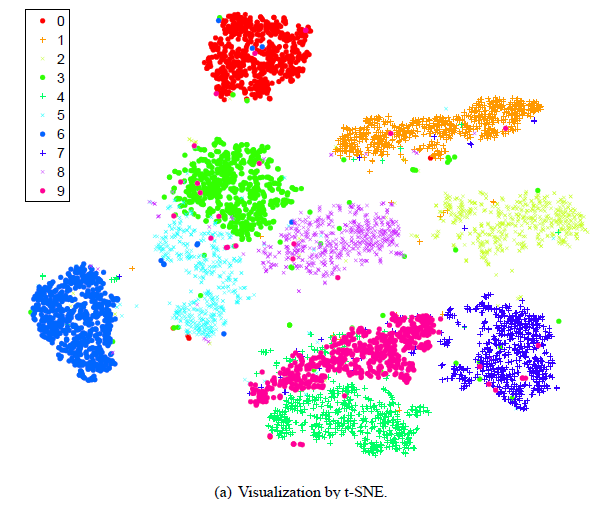
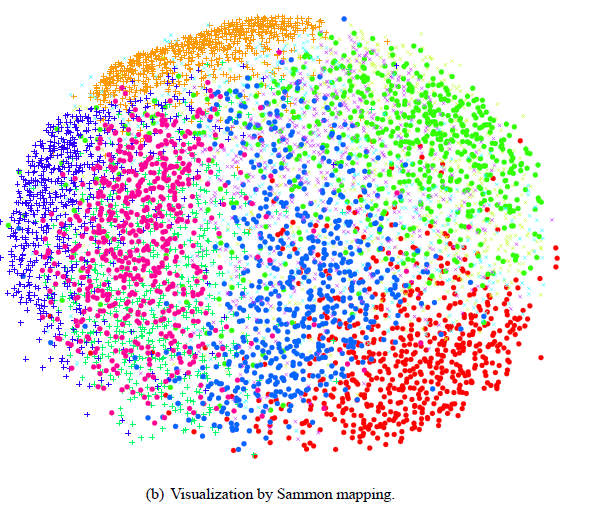
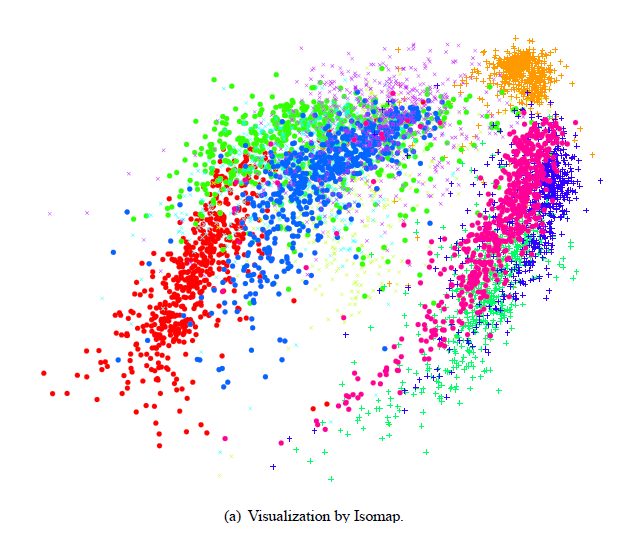
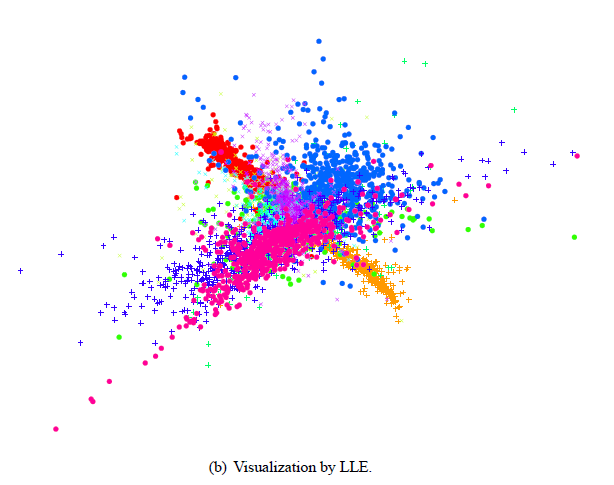
代码链接

先贴上源代码和PDF链接：

https://lvdmaaten.github.io/tsne/

使用说明

t-SNE函数使用示例：

mappedX = tsne(X, labels, no_dims, init_dims, perplexity);

参数说明

X：是数据集，尺寸为N*D，N行D列，每一行是一个样本点，每一个样本点是D维的；

labels：每一个样本对应一个label，因此labels这个变量也是N行；

no_dims：降维后的维度，默认为2维，即平面显示；

init_dims：样本的初始维度，如果不提供，就取D和50两者较小者。如果维度较高，程序默认使用PCA降维至30。

perplexity：默认30。

最后

以上就是飘逸大叔为你收集整理的t-SNE原理简述及matlab实现的全部内容，希望文章能够帮你解决t-SNE原理简述及matlab实现所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。