概述
数电——数制和码制
- 1. 概述
- 1.1 数字电路的发展历程
- 1.2 模拟信号和数字信号
- 1.2.1 对比
- 1.2.2 模拟信号
- 1.2.3 *数字信号
- 2. 几种常见的数制
- 2.1 数制的概念
- 2.2 *常见数制
- 2.2.1 十六进制
- 2.2.2 其他进制省略
- 3. *不同数制之间的转换
- 3.1 其他进制转换十进制的方式
- 3.2 十进制转换其他进制的方式
- 3.2.1 十进制转换成二进制
- 常规方法
- 快速方法
- 3.2.2 十进制转换成八进制，十六进制
- 3.2.3 二进制转换成八进制，十六进制
- 4. *二进制算术运算
- 4.1 二进制运算特点
- 4.2 反码，补码，补码运算
- 4.2.1 原码，反码，补码
- 5. 几种常见的编码
- 5.1 三个术语
- 5.2 分类
- 5.2.1 *二-十进制编码
- 5.2.2 *二进制编码
- 5.2.3 二进制代码
- 作业
- 备注：
1. 概述
1.1 数字电路的发展历程
数字技术是一门应用学科，他的发展可以分为5个阶段：
| 阶段 | 时间 | 主要内容 |
|---|---|---|
| 产生 | 20c30s | 20c30c计算机引入二进制存储方式；1847年乔治·布尔创立的布尔代数得到应用 |
| 初级阶段 | 20c40s | 电子管（真空管）得到应用，电话，数字通讯 |
| 第二阶段 | 20c60s | 晶体管得到应用，计算机，测量 |
| 第三阶段 | 20c70s中期 | 集成电路出现，各个领域得到应用 |
| 第四阶段 | 20c70s中-80s中 | 微电子技术，大规模超大规模集成电路 |
| 第五阶段 | 20c80s中以后 | 产生专用，通用集成芯片，使得数字电路的设计模块化可编程化，提高性能，适用性，降低成本 |
1.2 模拟信号和数字信号
1.2.1 对比
| 模拟信号 | 数字信号 |
|---|---|
| 时间或是数值上连续1 | 时间,数值都离散 |
1.2.2 模拟信号
1.2.3 *数字信号
产生，传输，处理 数字信号的电路称之为数字电路
数字信号包括 电平型 和 脉冲型2
| 脉冲信号 | 电平信号 |
|---|---|
| 周期信号，有时间周期 | 与时间无关 |
| 有脉冲为“1”，无脉冲为“0” | 高电平为“1”，低电平为“0” |
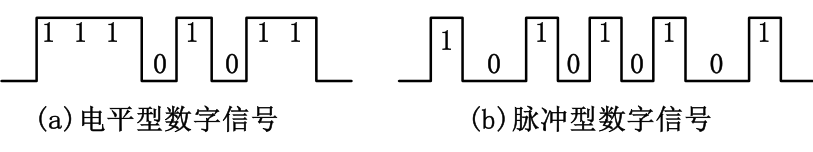
2. 几种常见的数制
2.1 数制的概念
计数方法，把多位数码每一位的构成方法和低位到高位的进位规则称为数制
通过一个笑话来展现进制的好处:
世界上有10种人，一种是懂二进制的人，另外一种人则不懂
2.2 *常见数制
常见的数制有十进制（D-Decimal）,二进制（B-Binary），八进制（O-Octal），十六进制（H-Hexadecimal）
2.2.1 十六进制
用
A
,
B
,
C
,
D
,
E
,
F
A,B,C,D,E,F
A,B,C,D,E,F分别表示
10
,
11
,
12
,
13
,
14
,
15
10,11,12,13,14,15
10,11,12,13,14,15
目前计算机通常是采用8位，16位，32位二进制表示和计算，他们分别可以用2位，4位，8位十六进制表示，所以比较方便
2.2.2 其他进制省略
3. *不同数制之间的转换
3.1 其他进制转换十进制的方式
(
D
)
N
=
k
n
−
1
k
n
−
2
.
.
.
k
0
k
−
1
.
.
.
k
−
m
=
k
n
−
1
∗
N
n
−
1
+
k
n
−
2
∗
N
n
−
2
+
.
.
.
k
0
∗
N
0
+
k
−
1
∗
N
−
1
+
.
.
.
k
−
m
∗
N
−
m
=
∑
i
=
−
m
n
−
1
k
i
∗
N
i
(D)_{N} = k_{n-1}k_{n-2}...k_{0}k_{-1}...k_{-m}\=k_{n-1}*N^{n-1}+k_{n-2}*N^{n-2}+...k_{0}*N^{0}+k_{-1}*N^{-1}+...k_{-m}*N^{-m}\=sum_{i=-m}^{n-1}k_{i}*N^{i}
(D)N=kn−1kn−2...k0k−1...k−m=kn−1∗Nn−1+kn−2∗Nn−2+...k0∗N0+k−1∗N−1+...k−m∗N−m=i=−m∑n−1ki∗Ni
N称为基数，
k
i
k_{i}
ki表示系数，
N
i
N^{i}
Ni表示第
i
i
i位的权值
3.2 十进制转换其他进制的方式
十进制转成二进制，再通过二进制转换成八进制和十六进制
3.2.1 十进制转换成二进制
常规方法
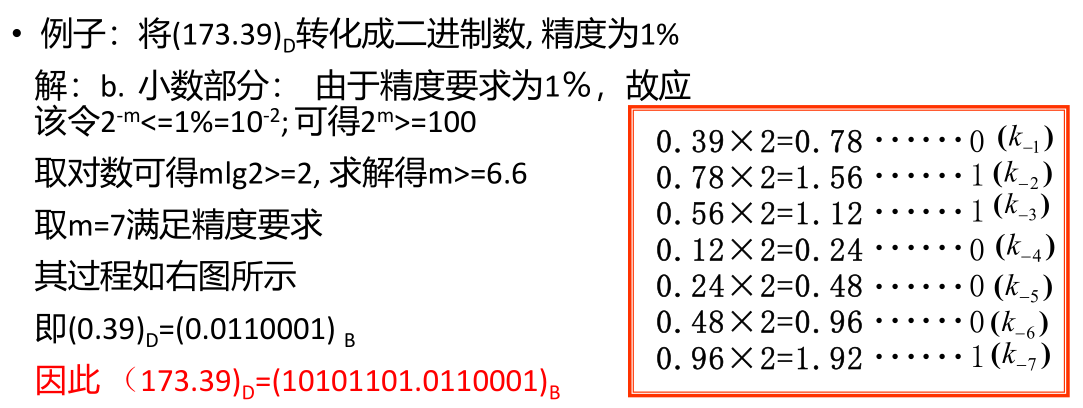
小数部分
2
−
m
<
=
1
0
−
2
,
2
m
>
=
100
,
2
6
<
2
m
<
2
7
,
2^{-m}<=10^{-2},2^{m}>=100,2^{6}<2^{m}<2^{7},
2−m<=10−2,2m>=100,26<2m<27,所以m应该取7，应该有7位小数位
快速方法
- 如果对二进制数熟悉的话，可以将十进制拆分成二进制数的和
例如：14=8+4+2，0.75=0.5+0.25
这样子可以直接写出对应的二进制数 - 对于精度的要求则直接找到比精度小的
3.2.2 十进制转换成八进制，十六进制
与十进制转换成二进制类似，把基数换成别的就ok。
不过更常用的方式是用 10->2->其他
3.2.3 二进制转换成八进制，十六进制
每三位二进制转换成一位八进制，每四位二进制转换成一位十六进制
每一位八进制转换成三位二进制，一位十六进制转换成四位二进制
4. *二进制算术运算
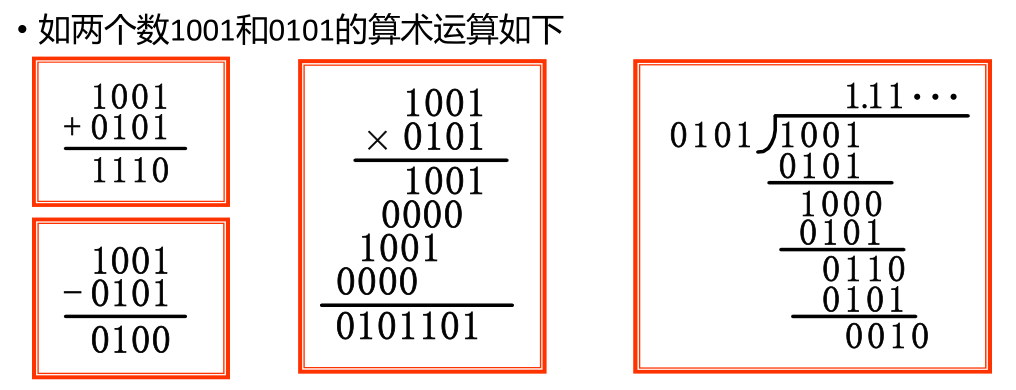
4.1 二进制运算特点
4.2 反码，补码，补码运算
4.2.1 原码，反码，补码
8位二进制数包含了符号位
| 原码 | 反码 | 补码 |
|---|---|---|
| 带符号位二进制数 | 正数原码是原码，负数除了符号位，全部取反 | 正数补码为原码，负数是反码加1 |
| 0 111 | 0 111 | 0 111 |
| 1 111 | 1 000 | 1 001 |
之所以引入补码，是为了简化运算，计算机进行加减时不需要再进行符号判断，减法运算也可以通过加法实现
反码与补码的“0”：+0的反码是0000，-0的反码是1111,0的补码只有一个0000
已经知道补码求原码：
正数一样；
负数：减一取反==取反加一（所有变换都是针对数值位，符号位不变）
补码的乘除法忘了差不多了，对不起lzh老师
5. 几种常见的编码
5.1 三个术语
| 数码 | 代表一个确切的数字，如二进制数 |
| 代码 | 特定的二进制数码组，代表不同的信号，不一定是数字 |
| 编码 | 是指给用数字代表特定信息的过程，也可以看成一套规则 |
5.2 分类
二进制编码，二-十进制编码
有权码，无权码
5.2.1 *二-十进制编码
用4位二进制数表示十进制数的编码方式叫做二-十进制编码
余3码、余3循环为无权的二-十进制编码
8421码、2421码、5211码为有权二-十进制编码，即每一位的1都代表固定的值
| 编码 | 定义 | 是否有权 | 优点 |
|---|---|---|---|
| 8421码 | 又称Binary-Coded Decimal code，每一位对应的权值分别是8421 | 有权码 | 与二进制对应，简单方便 |
| 2421码 | 其每位的权为2、4、2、1；1111就是9 | 有权码 | 与余3码相同，0和9、1和8、2和7…是互为反码 |
| 2421码 | 其每位的权为5、2、1、1；1111就是9 | 有权码 | 主要用在分频器上 |
| 余三码 | 按二进制转成十进制得到的数比对应的十进制大3，比如0011对应的是0 | 无权码 | 余三码相加自动进位，0和9、1和8、2和7…是互为反码，求补方便 |
| 余三循环码 | 无权码 | 从格雷码截取，比如0，就是十进制3对应的格雷码，相邻的两个代码之间只有一位状态不同 | 这在译码时不会出错（竞争－冒险） |
5.2.2 *二进制编码
自然码和循环码
- 自然码，有权码，结构形式与二进制相同
- 循环码，也叫格雷码，无权码，特点是任何相邻的两个码组中，仅有一位代码不同，抗干扰能力强，主要用在计数器中
格雷码的变化规律，0000，低位开始，每次只变一位，0001,0011,0010,低位变完高位变，0110
5.2.3 二进制代码
ASCII码(American Standard Code for Information Interchange，美国信息交换标准代码）是基于拉丁字母的一套电脑编码系统。
作业
出现的问题：容易因为粗心犯错，还有就是补码原码那一块的符号位小心一点
备注：
这个和王老师课件上不太一样，我看了参考书《数字电子技术基础.(阎石.第5版)》的概述，里面对模拟信号的描述是说“另外一类物理量在时间或是数值上是连续的，我们把这一类物理量成为模拟量”。 ↩︎
对于脉冲和电平还是不太理解 ↩︎
最后
以上就是阳光春天为你收集整理的数电1——数制和码制1. 概述2. 几种常见的数制3. *不同数制之间的转换4. *二进制算术运算5. 几种常见的编码作业的全部内容，希望文章能够帮你解决数电1——数制和码制1. 概述2. 几种常见的数制3. *不同数制之间的转换4. *二进制算术运算5. 几种常见的编码作业所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复