文章目录
- 1 进制转换
- 2 定点数表示及其运算
- 2.1 定点数表示
- 2.1.1 真值→补码
- 2.1.2 补码→真值
- 2.1.3 [XT]补 →[-XT]补
- 2.1.4 真值、原码、反码、补码转换关系图形总结
- 2.2.4 移码
- 2.2 定点数运算
- 2.2.1 移位运算
- 2.2.2 定点数加减运算
- 2.2.3 溢出判断
- 判溢出方法一
- 判溢出方法二
- 判溢出方法三
- 3 浮点数及其运算
- 3.1 浮点数表示
- 3.2 浮点数规格化
- 3.3 规格化浮点数的特点
- 3.4 IEEE754 标准
- 3.5 浮点数加减
- 3.5.1 浮点数的加减运算实例
- 3.5.2 舍入
- 3.6 浮点数强制类型转换
1 进制转换
任意进制→十进制
已知K、r、n
按权展开相加法
十进制→任意进制
除基取余法:
乘基取整法:
进制之间的转换
分组转换:
2n进制之间的转换:二进制、四进制、八进制、十六进制二进制一>四进制、八进制、十六进制
n位一组,每组转换成对应进制的符号,位数不够补左边最高位0和右边最低位0
四进制、八进制、十六进制一>二进制
每位写成对应的二进制形式
BCD码
用途:可以实现二进制,十进制的快速转换(一一对应)
8421码,4位一组的二进制表示十进制对应的符号
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 |

遇到8421码某组上的计算产生超过1001时,需进行加6(0110)进行结果修正
2 定点数表示及其运算
小数点位置约定在固定位置的数称为定点数
小数点位置约定为可浮动的数称为浮点数
2.1 定点数表示
定点数可分为无符号数和有符号数
- 无符号数:整个机器字长的全部二进制位均为数值位,没有符号位,相当于数的绝对值。
- 无符号数表示范围:n位的无符号数表示范围为:0~2n-1
有符号数对应真值和机器数
真值和机器数

2.1.1 真值→补码
- 正数:[X]原=[X]反=[X]补 正数原反补一样
- 负数:
求补码:原符号位不变,数值部分按位取反,末尾+1
求反码:符号位不变,数值位按位取反
2.1.2 补码→真值
按位取反+1
[XT]补 =1 0110100
[XT]= -(1001011+1)= -1001100
2.1.3 [XT]补 →[-XT]补
连同符号位各位取反,末尾+1
[XT]补=1 0110100
[-XT]补= 0 1001100
2.1.4 真值、原码、反码、补码转换关系图形总结
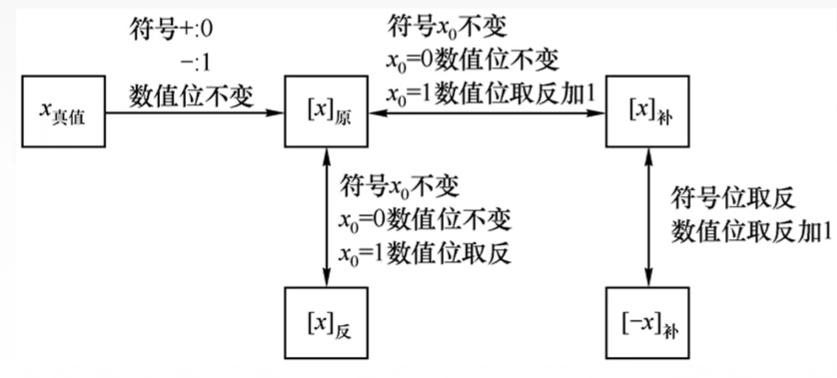
2.2.4 移码
浮点数阶码用移码表示,移码只用来表示定点整数
设E为阶码,阶码的移码表示位n位,[E]移=2n-1+E(2n-1为偏置常数)
2.2 定点数运算
2.2.1 移位运算
r进制右移n位:÷ rn
左移n位: × rn
-
机器数采用无符号数:逻辑移位
逻辑左移时,高位移丢,低位添0;逻辑右移时,低位移丢,高位添0 -
机器码采用有符号数:算术移位
算术移位:左移相当于乘以基数,右移相当于除以基数
符号位不参与移位
1,0110101 真值-53
左移1位(丢0):1,110101 0 真值-106
右移1位(丢1):1,0 011010 真值-26 假设不丢1:1,0011010.1 真值-26.5
再左移1位(丢1):1,1010100 真值-84 假设不丢1:1,111010100 真值-212
再右移1位(丢0):1,0001101 真值-13
结论:原码算术移位:左移丢1,运算出错;右移丢1,影响精度。
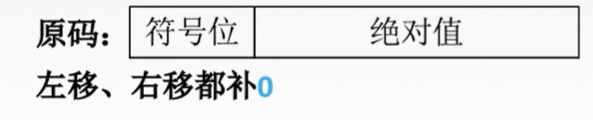
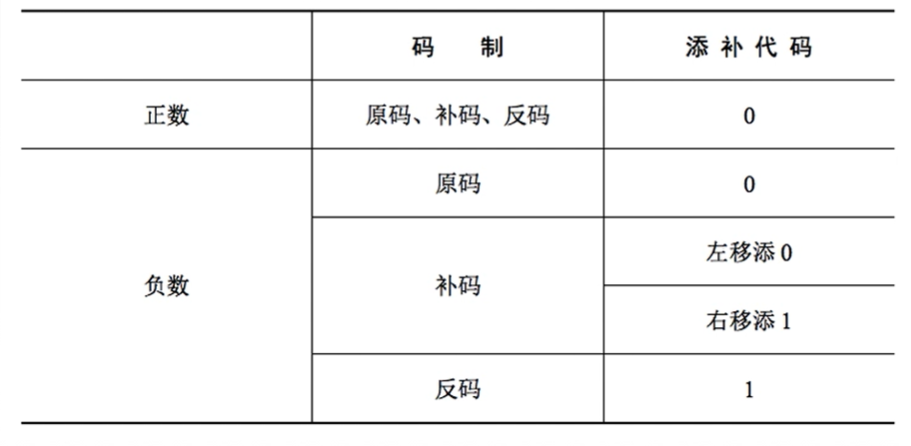
正数:原码、补码、反码一样→左移、右移都补0
负数:反码1<——>原码0
2.2.2 定点数加减运算
补码的主要作用:两个有符号数可以直接相加
加减运算基本思路:
- 转换成x+y的形式
- 计算[x]补+[y]补
例题:设机器字长为8位(含1位符号位),A=15,B=-24,求[A+B]补和[A-B]补
走捷径:十进制运输完毕将结果转换为补码

也可以先转化为补码,再将补码进行符号扩展

[A+B]补=[A]补+[B]补=0,0001111+1,1101000=1,1110111
补码1,1110111,对应原码:1,0001001 真值就是-9,15+(-24)=-9
[A-B]补=[4]补+[-B]补=0,0001111+0,0011000=0,0100111
补码0,0100111对应真值+39,15-(-24)=+39
[-B]补:[B]补连同符号位一起取反加1
2.2.3 溢出判断
正溢出:两个正数做加法得负数
负溢出:两个负数做加法得正数
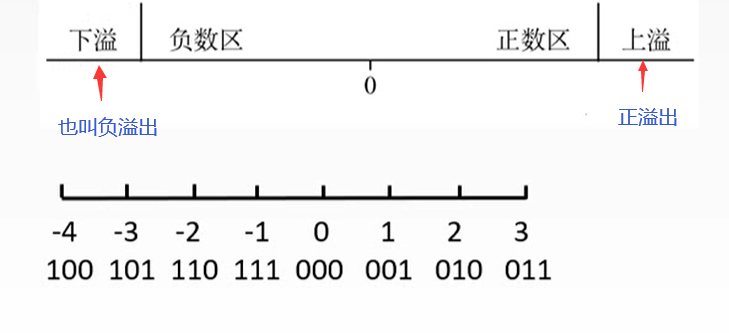
例:A=15,B=-34,C=124,求[A+C]补和[B-C]补
[A+C]补=0 0001111+0 1111100=1 10001011 真值-11→正溢出
[B-C]补=1 101000+0 000100=10 1101100 真值+108→负溢出
判溢出方法一
采用一位符号位设A的符号为As,B的符号为Bs,运算结果的符号为Ss,则溢出逻辑表达式为
V表示含义:[As为1且Bs为1且Ss为0] 或 [As为0且Bs为0且Ss为1]若V=0,表示无溢出;
若V=1,表示有溢出。
补充逻辑表达式:
- 与:如ABC,表示A与B与C仅当A、B、C均为1时,ABC为1
A、B、C中有一个或多个为0,则ABC为0- 或:如A+B+C,表示A或B或C仅当A、B、C均为0时,A+B+C为0
A、B、C中有一个或多个为1,则A+B+C为1
判溢出方法二
采用一位符号位,根据数据位进位情况判断溢出
| 符号位的进位Cs | 最高数位的进位C1 | |
|---|---|---|
| 正溢出 | 0 | 1 |
| 负溢出 | 1 | 0 |
即:Cs与C1不同时有溢出
处理“不同”的逻辑符号:异或
溢出逻辑判断表达式为:
若V=0,表示无溢出;
V=1,表示有溢出。
补充异或:
判溢出方法三
采用双符号位,配合补码
正数符号为00,负数符号为11
[A+C]补=00,0001111+00,1111100=01,0001011→正溢出
[B-C]补=11,1101000+11,0000100=10,1101100→负溢出
记两个符号位为Ss1Ss2,则
若V=0,表示无溢出;
若V=1,表示有溢出。
利用双符号位计算[A+B]补和[A-B]补
[A+B]补=00,0001111+11,1101000=11,1110111
[A-B]补=00,0001111+00,0011000=00,0100111
采用双符号位的移位运算:低位符号位参与移位,高位符号位代表真正的符号
11,1110111 右移1位: 11,1111011 //低位符号位参与右移,对于负数补码,符号位空出的部分补1
00,0100111 左移1位: 00,1001110 //左移一位,数值位最高位0移到符号位低位,数值位低位空出的部分则补0
00,0100111 左移2位: 01,0011100 正溢出
3 浮点数及其运算
3.1 浮点数表示
任意一个二进制数X可以表示为: X=(-1)S× M × RE
S取值为0或1,用来决定X的符号
M是一个二进制定点小数,称为数X的尾数
E是一个二进制定点整数,称为X的阶码或指数
R是基数,可以取值为 2、4、16
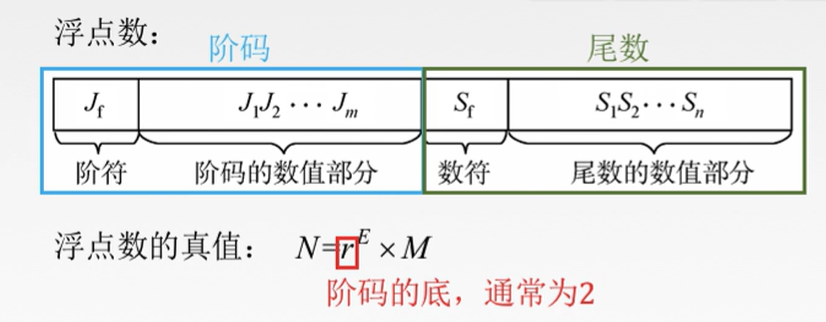
阶码:常用补码或移码表示
尾数:常用原码或补码表示
阶码E反映浮点数的表示范围及小数点的实际位置;尾数M的数值部分的位数n反映浮点数的精度。
例:阶码、尾数均用补码表示,求b的真值

如果尾数部分只存储1001,怎么处理?----→规格化

3.2 浮点数规格化
规格化:规定尾数的最高数位必须是一个有效值。对于二进制来说最高位数1有效,对于其他进制,不是0则有效
左规:当浮点数运算的结果为 非规格化时 要进行规格化处理,将尾数左移一位,阶码减1(基数为2时)。
右规:当浮点数运算的结果尾数出现 溢出(双符号位为01或10) 时,将尾数右移一位,阶码加1(基数为2时)。
例:a=010;00.1001,b=010;00.1000,求a+b
a=22 × 00.1001; b=22 × 00.1000
a+b=22 × 00.1001+22 × 00.1000
=22 ×(00.1001+00.1000)
=22 × 01.0100 →尾数溢出,右规
=23 × 00.1010
3.3 规格化浮点数的特点
规格化浮点数的尾数M的绝对值应满足:1/r<|M|<1
如果r=2,则有1/2<M<1
- 原码规格化后:
- 正数为0.1××…×的形式,其最大值表示为0.11…1;最小值表示为0.10…0。
尾数的表示范围为 1/2≤M≤(1-2-n)。- 负数为1.1××.…×的形式,其最大值表示为1.10…0;最小值表示为1.11…1。
尾数的表示范围为 -(1-2-n)≤M≤ -1/2。
- 补码规格化后:
- 正数为0.1××…×的形式,其最大值表示为0.11…1;最小值表示为0.10…0。
尾数的表示范围为 1/2≤M≤(1-2-n)。- 负数为1.0××.…×的形式,其最大值表示为1.01…1;最小值表示为1.00…0。
尾数的表示范围为 -1≤M≤ -(1/2+2-n)。
3.4 IEEE754 标准

尾数规格化,最高位肯定为1,若尾数原码
xx...x,则尾数是1.xx...x
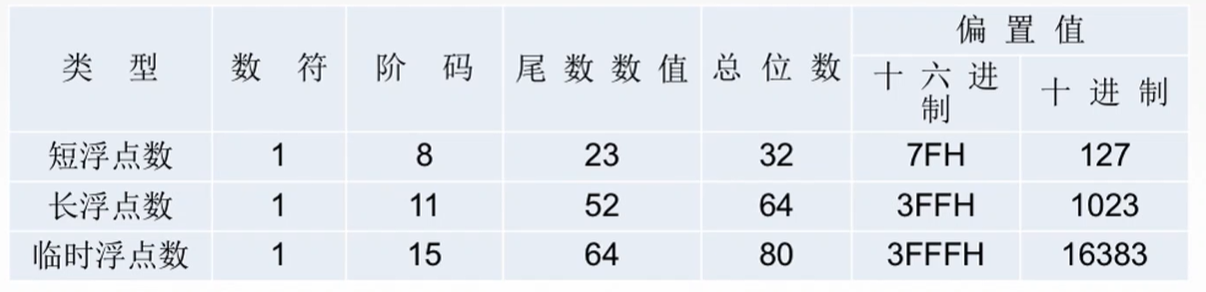
阶码部分用移码表示的,由移码得真值要减去偏置值
短浮点数:
长浮点数:
IEEE754 标准下短浮点数和长浮点数的真值:

IEEE 754 标准一些规定(短浮点数为例):
- E=0且M=0,则真值为0
- E=0且M≠0,为非规格化数,真值 =(-1)s×0.M×2-126
- 1≤E≤254时,真值 =(-1)s×1.M×2E-127
- E=255且M≠0时(阶码全1,尾数不为0),真值为
NaN(非数值)- E=255且M=0时,真值为正无穷或负无穷(看符号位)

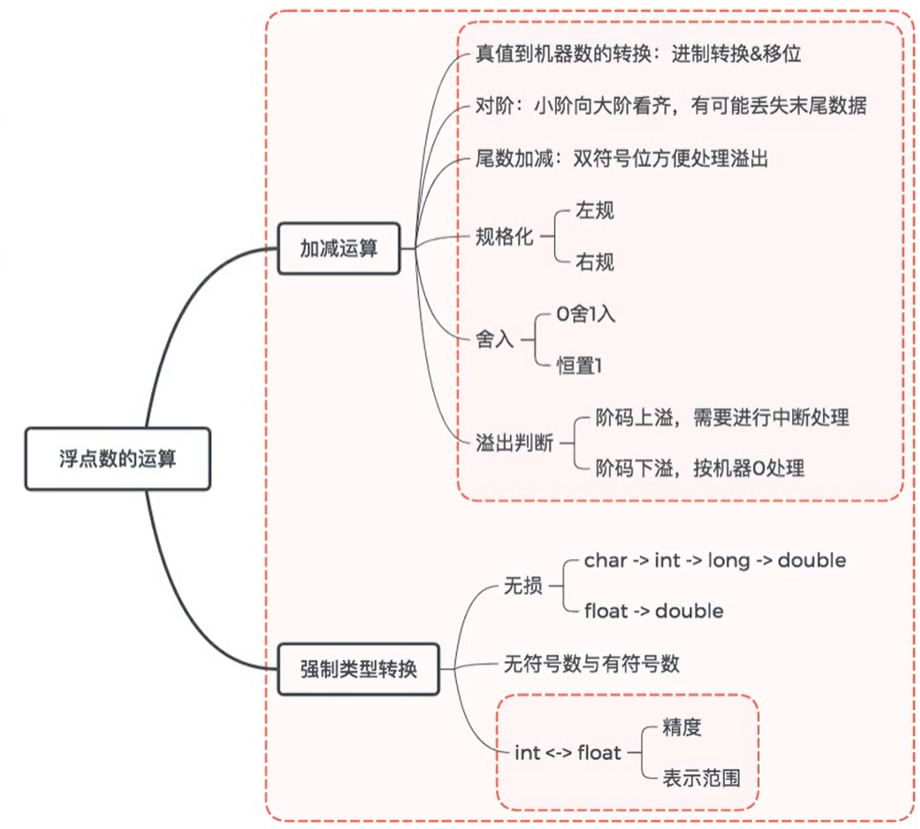
3.5 浮点数加减
浮点数加减运算步骤:
- 对阶
一般在对阶之前就有必须要把真值转化为机器数的步骤(即用补码表示阶码和尾数)
- 尾数加减
- 规格化
- 舍入
- 判溢出
3.5.1 浮点数的加减运算实例
例:已知十进制数X=-5/256、Y=+59/1024,按机器补码浮点运算规则计算X-Y,结果用二进制表示,浮点数格式如下:阶符取2位,阶码取3位,数符取2位,尾数取9位
- 先进行格式转换:用补码表示阶码和尾数
- 将X的阶码转化为机器数:-101 补码:1 011,再变为双符号位(阶符取两位): 11 011(11 代表负,00代表正),数值部分(阶码)3位不需要扩展
- 将X的尾数转化为机器数:-0.101 补码:1.011 ,再变为双符号位(数符取两位):11.011,尾数取9位则扩展到9位:11.011000000(小数低位添0,整数高位添0)
转化完毕X,Y机器数表示:X:11 011,11.011000000 ;Y:11 100,00.111011000
转化完接下来就是对阶
- 对阶
对阶目的:使两个数的阶码相等,小阶向大阶看齐,尾数每右移一位,阶码加1①求阶差:[△E]补=[X阶]补+[-Y阶]补=11011+00100=11111,知△E=-1(被减的数转化为相反数的补码形式,即[Y]补→[-Y]补→连同符号位按位取反,末尾+1)
②对阶X 向Y看齐:X:11011,11.011000000→11100,11.101100000(X尾数右移1位,阶码+1)
尾数左移/右移:双符号位也要参与移位
接下来进行尾数加减,原理就是提取公因式
- 尾数加减
求 X-Y,先求-Y补码:阶码部分不变,尾数调整为相反数补码,即连同符号位按位取反,末尾+1
[-Y]补:11100,11.000101000
X-Y=11100,10.110001000
机器数操作不理解,可以把真值操作写在旁边对比:
算出的结果符号位10,溢出了,需要右规
- 规格化
X-Y:11100,10.110001000→11101,11.011000100
对应真值运算:
- 规格化之后,观察阶码阶符是否还保持正常情况(00或11),则此次运算不溢出,若规格化后,双符号位表现出溢出模式(10或 01),此次运算一定溢出!
- 在加减处溢出不一定是溢出,只有在规格化以后还是溢出,才是真正溢出!
- 舍入
这里无舍入,因为尾数右移时候,末尾丢的是一个0,不影响整个数值运算
- 判溢出
此处正常阶码11,无溢出
所以结果真值为2-3×(-0.1001111)2
3.5.2 舍入
- “0”舍“1”入法:类似于十进制数运算中的“四舍五入”法,即在尾数右移时,被移去的最高数值位为0,则舍去;被移去的最高数值位为1,则在尾数的末位加1。这样做可能会使尾数又溢出,此时需再做一次右规。
- 恒置“1”法:尾数右移时,不论丢掉的最高数值位是“1”还是“0”,都使右移后的尾数末位恒置“1”。这种方法同样有使尾数变大和变小的两种可能。
例:两浮点数加减后结果为11100,10.110001011。此时肯定需要右规
采用0舍1入:11100,10.110001011→11101,11.011000101 1(末尾1丢弃,需要+1)
→11101,11.011000110 (末尾+1后进位)
恒置1:11100,10.110001011→11101,11.011000101 1
→11101,11.011000101 1
3.6 浮点数强制类型转换
| 类型 | 16位机器 | 32位机器 | 64位机器 |
|---|---|---|---|
| char | 8 | 8 | 8 |
| short | 16 | 16 | 16 |
| int | 16 | 32 | 32 |
| long | 32 | 32 | 64 |
| long long | 64 | 64 | 64 |
| float | 16 | 32 | 32 |
| double | 64 | 64 | 64 |
char →int→long →double
float →double
范围、精度从小到大,转换过程没有损失
32位
int:表示整数,范围-231-231-1,有效数字32位
float:表示整数及小数,范围 士[2-126 ~~ 2+127×(2-2-23)],有效数字23+1=24位
int→float:可能损失精度
float →int:可能溢出及损失精度
最后
以上就是娇气身影最近收集整理的关于2 计算机组成原理第二章 数据的表示和运算 定点数运算 浮点数运算的全部内容,更多相关2内容请搜索靠谱客的其他文章。




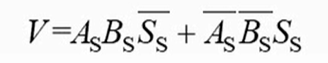


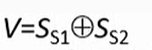







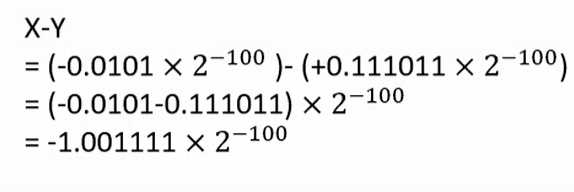









发表评论 取消回复