1.乘基取整法

如小数部分=0.3D

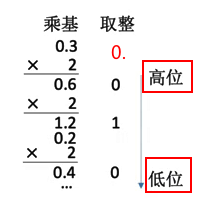
0.3D=0.010B

2.BCD码

用二进制编码的十进制，可能有冗余

2.18421码

映射关系：

手算方法：

机算方法：

2.2余3码

映射关系：8421码+(0011)₂

2.32421码

映射关系：改变权值定义，0-4二进制首位为0,5-9二进制首位为1

3.字符与字符串

3.1汉字的表示和编码

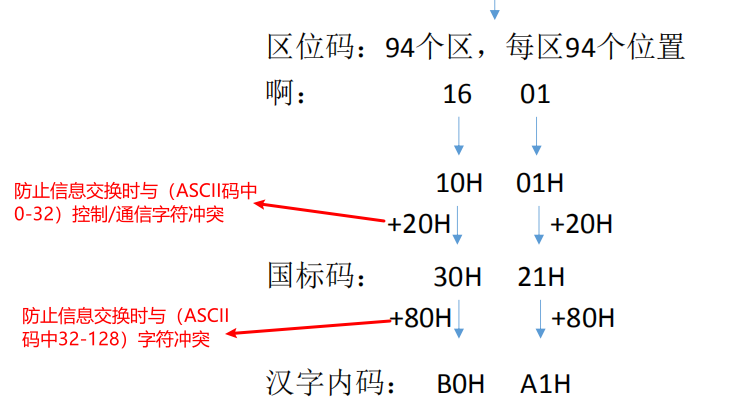
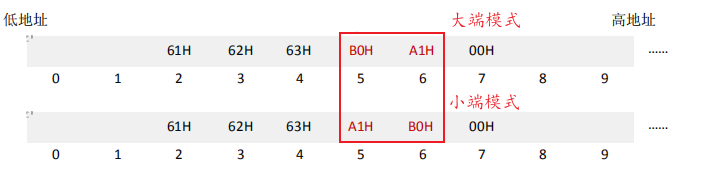
3.2大端模式和小端模式

大端模式：将数据的最高有效字节存放在低地址单元中
小端模式：将数据的最高有效字节存放在高地址单元中
以下以B0 A1H为例，我们平常按顺序写的就是大端模式

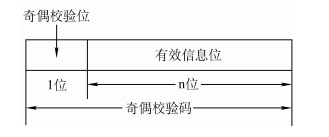
4.奇偶检验码（仅能检测出奇数位错误，无纠错能力）

4.1码的基本概念

码字:由若干位代码组成的一个字叫码字。

将两个码字逐位进行对比，具有不同的位的个数称为两个码字间的距离。一种编码方案可能有若干个合法码字，各合法码字间的最小距离称为码距。

★当d=1时，无检错能力；当d=2时，有检错能力；当d≥3时，若设计合理，可能具有检错、纠错能力。（系统一般只会跳变一位，但是码距为2，这串代码就变成了一个非法状态，编码不存在，所以有检错能力，码距为3是就可以设计方案实现纠错功能。）

4.2奇偶检验码

奇校验码：整个校验码（有效信息位和校验位）中“1”的个数为奇数。
偶校验码：整个校验码（有效信息位和校验位）中“1”的个数为偶数。

4.2.1例题

4.2.2硬件实现

偶校验的硬件实现:
①各信息进行异或（模2加）运算，得到的结果即为偶校验位。
②所有位进行异或，若结果为1说明出错

5.海明校验码（纠错1位，检错2位）

设信息位：1010

5.1确定校验位个数(k个校验位，n个信息位)

2^k ≥ n + k + 1
n = 4 —> k = 3
设信息位D4D3D2D1（1010），共4位，校验位P3P2P1， 共3位，对应的海明码为H7H6H5H4H3H2H1。

5.2 确定校验位的分布

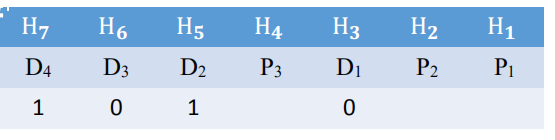
校验位Pi放在海明位号为2ⁱ −1的位置上,信息位按顺序放到其余位置

5.3求校验位的值

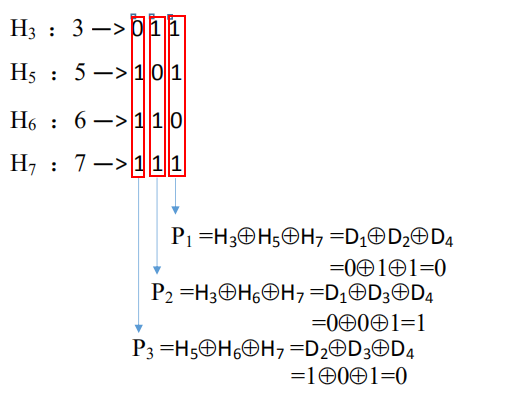
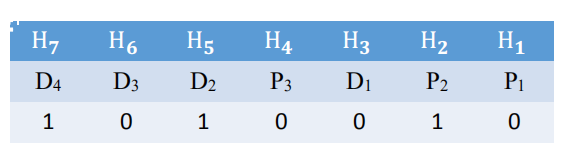
5.4纠错

s3 s2 s1 = 000说明无错误
s3 s2 s1 ≠ 000，则其值反映出错位置

5.5补充

奇数个1异或为1，偶数个1异或为0
海明码无法区分到底是1位错还是2位错，需加上“全校验位”，对整体进行偶校验

6.循环冗余校验码

设生成多项式为G(x)=x³+x²+1，信息码为101001，求对应的CRC码。

6.1确定K（信号位）、R（校验位）以及生成多项式对应的二进制码

K = 信息码的长度 = 6，R = 生成多项式最高次幂 = 3→校验码位数N = K + R = 9

生成多项式G(x) = x³+x²+1，对应二进制码1101

6.2移位补0

信息码左移R位，低位补0

6.3相除

对移位后的信息码，用生成多项式进行模2除法，产生余数

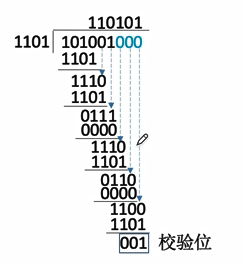
对应的CRC码：101001 001

6.4检错和纠错

发送：101001001
接收：101001001 用1101进行模2除 余数为000，代表没有出错
接收：101001011 用1101进行模2除 余数为010，代表出错

6.5补充

1）可检测出所有奇数个错误；
2）可检测出所有双比特的错误；
3）可检测出所有小于等于校验位长度的连续错误；
4）若选择合适的生成多项式，2^R ≥ K+R+1（这个式子就是海明码那个）,则可纠正单比特错

最后

以上就是长情书本为你收集整理的2.1码的知识理解1.乘基取整法2.BCD码3.字符与字符串4.奇偶检验码（仅能检测出奇数位错误，无纠错能力）5.海明校验码（纠错1位，检错2位）6.循环冗余校验码的全部内容，希望文章能够帮你解决2.1码的知识理解1.乘基取整法2.BCD码3.字符与字符串4.奇偶检验码（仅能检测出奇数位错误，无纠错能力）5.海明校验码（纠错1位，检错2位）6.循环冗余校验码所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。