同步时序电路
同步时序电路中所有存储元件都在时钟脉冲CP的统一控制下,用触发器作为存储元件。几乎现在所有的时序逻辑都是“同步逻辑”:有一个“时钟”讯号,所有的内部记忆体(‘内部状态’)只会在时钟的边沿时候改变。在时序逻辑中最基本的储存元件是正反器。
同步逻辑最主要的优点是它很简单。每一个电路里的运算必须要在时钟的两个脉冲之间固定的间隔内完成,称为一个 ‘时钟周期’。只有在这个条件满足下(不考虑其他的某些细节),电路才能保证是可靠的。
同步逻辑也有两个主要的缺点:
- 时钟讯号必须要分布到电路上的每一个正反器。而时钟通常都是高频率的讯号,这会导致功率的消耗,也就是产生热量。即使每个正反器没有做任何的事情,也会消耗少量的能量,因此会导致废热产生。
- 最大的可能时钟频率是由电路中最慢的逻辑路径决定,也就是关键路径。意思就是说每个逻辑的运算,从最简单的到最复杂的,都要在每一个时脉的周期中完成。一种用来消除这种限制的方法,是将复杂的运算分开成为数个简单的运算,这种技术称为“流水线”。这种技术在微处理器中非常的显著,用来帮处提升现今处理器的时钟频率。1
按照输出特征的分类的同步时序电路
Moore型
即电路的总输出
Y
n
Y_n
Yn,只取决于各触发器的输出
Q
n
Q_n
Qn,而与外输入
X
n
X_n
Xn无关。即
Y
n
=
f
(
Q
i
)
Y_n=f(Q_i)
Yn=f(Qi)。
典型的电路图如下:
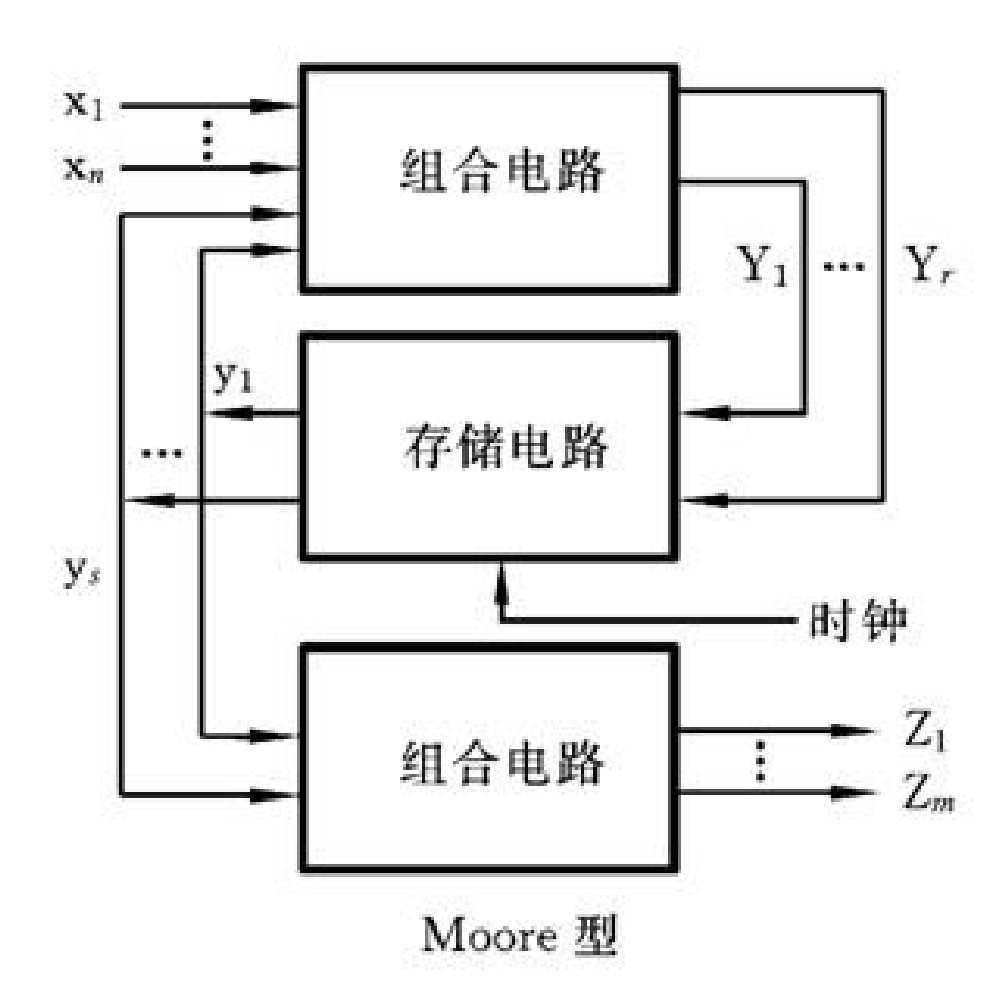
所有输出
Z
i
Z_i
Zi均基于存储电路(触发器组)的输出
Y
i
Y_i
Yi.
Mealy型
电路的输出
Y
n
Y_n
Yn不仅和存储电路的输出
Q
i
Q_i
Qi有关,还和当前时刻的输入
X
i
X_i
Xi有关.
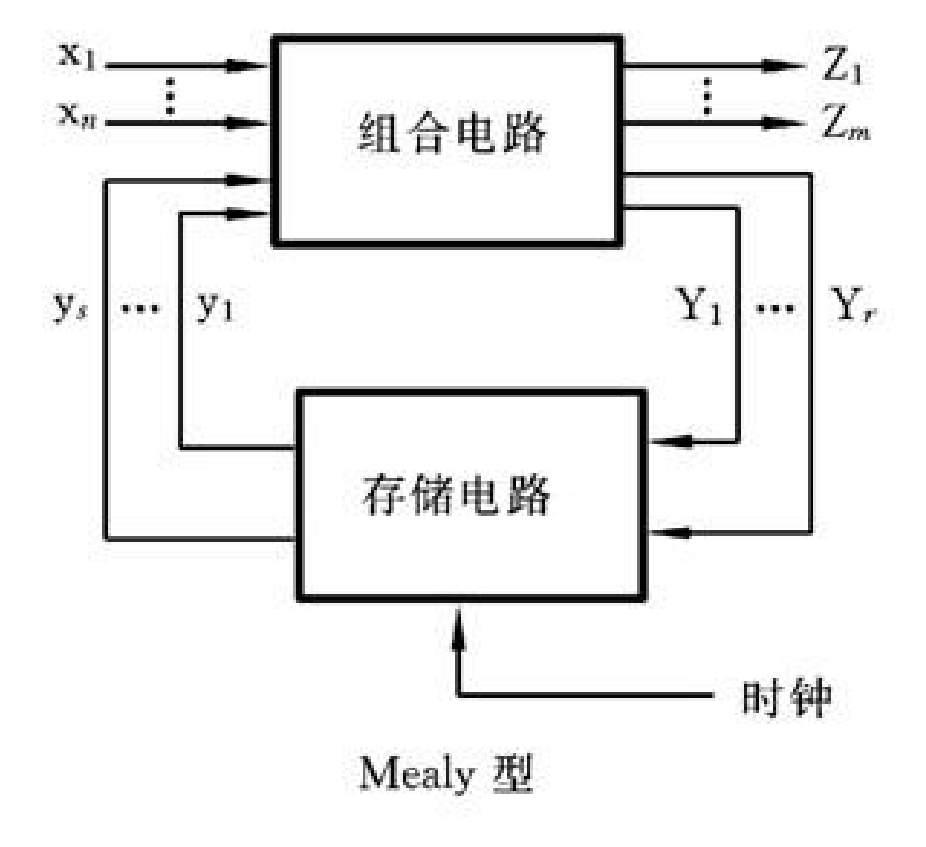
下面是一个典型的Mealy型电路:
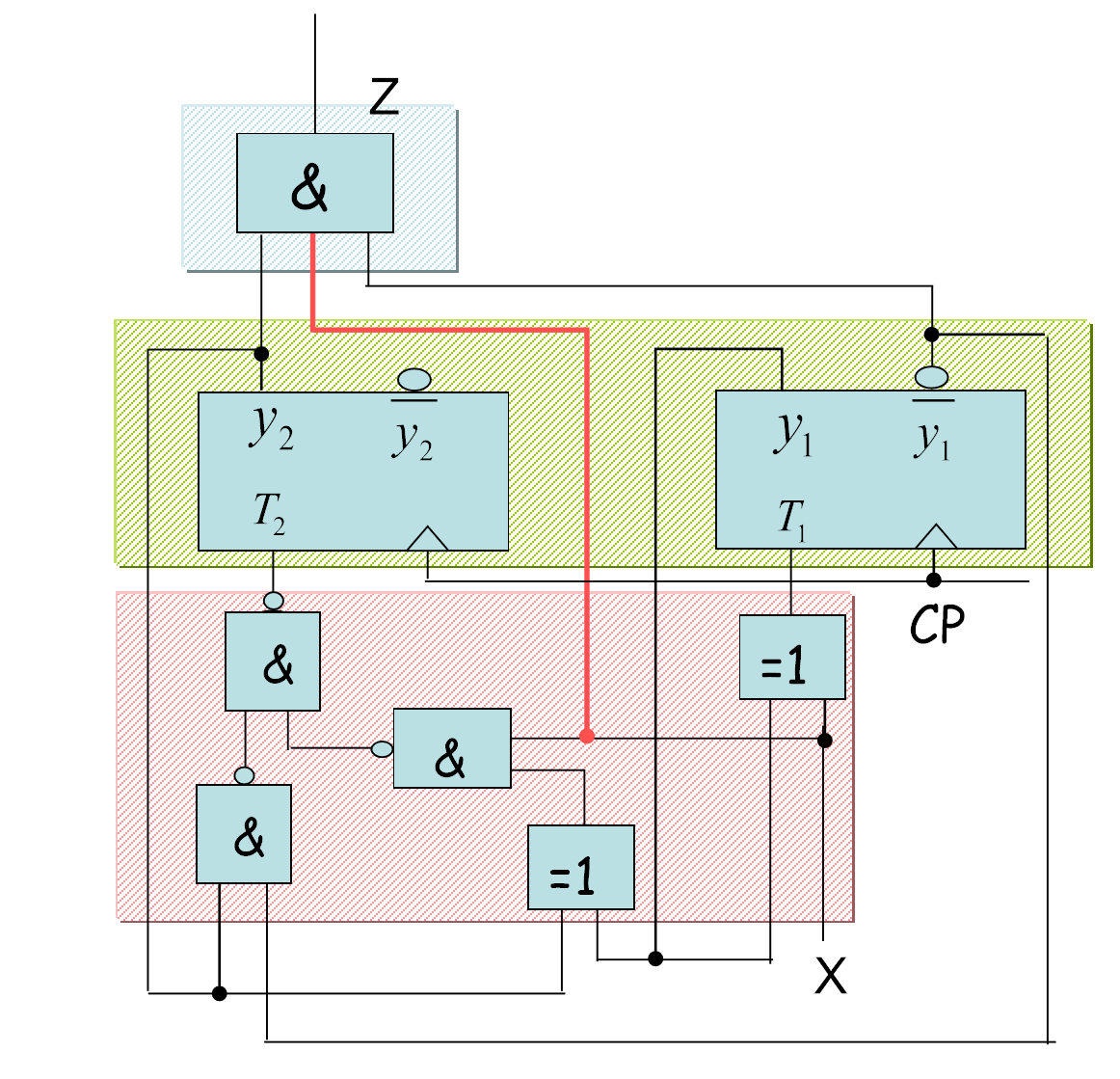
中间那个红线就是当前输出对于最终输出的影响.
时序电路的描述工具
表达式
| Moore | Mealy | Statements | |
|---|---|---|---|
| 输出函数表达式 | Z = f ( y i ) Z=f(y_i) Z=f(yi) | Z = f ( y i , x i ) Z=f(y_i,x_i) Z=f(yi,xi) | |
| 次态函数表达式 | y n + 1 = K ( y i , Y i ) y_{n+1}=K(y_i,Y_i) yn+1=K(yi,Yi) | y n + 1 = K ( y i , Y i ) y_{n+1}=K(y_i,Y_i) yn+1=K(yi,Yi) | 仅针对触发器的次态,根据类型不同参数也不同 |
| 激励函数表达式 | D = g ( y i , x ) D=g(y_i,x) D=g(yi,x) | D = g ( y i , x ) D=g(y_i,x) D=g(yi,x) | 也就是如何得到触发器输入的函数式 |
- 激励函数表达式表现如何从输入和触发器之前的记录得到新的触发器输入
- 次态函数表达式表现如何从输入得到新的触发器记录
- 输出函数表达式表现触发器输出的处理过程得到最后结果
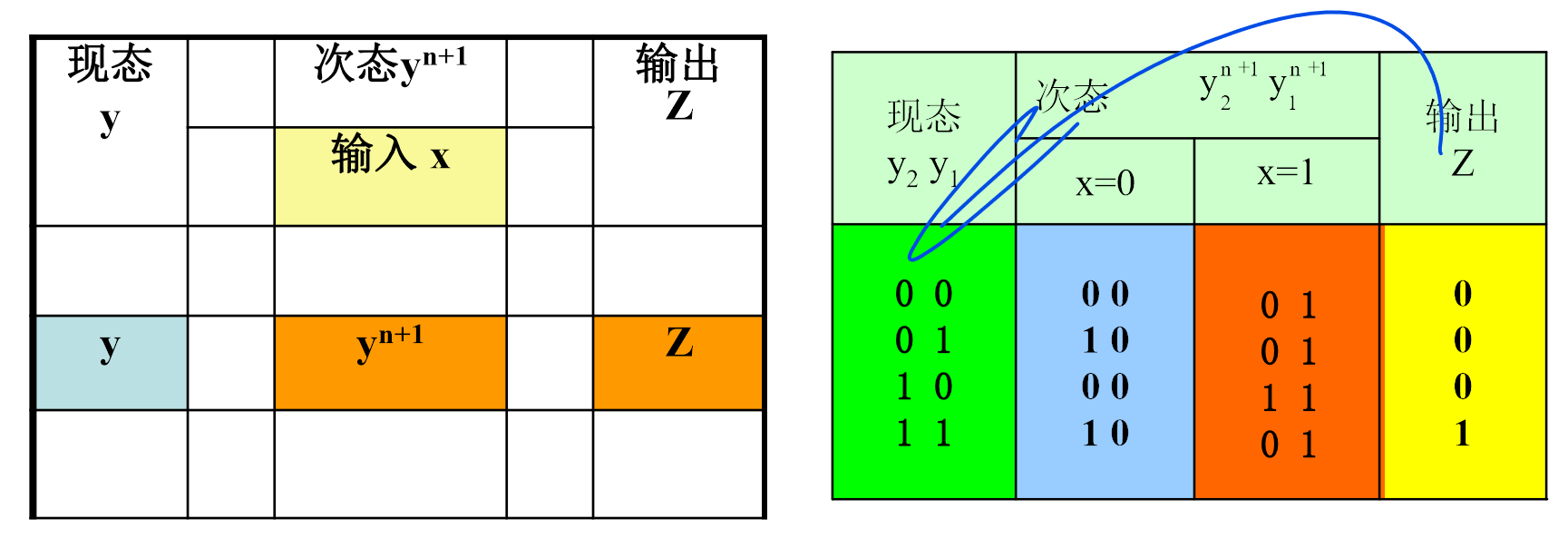
状态表
反映同步时序电路输出Z、次态yn+1与电路输入x、现态y 之间关系的表格.
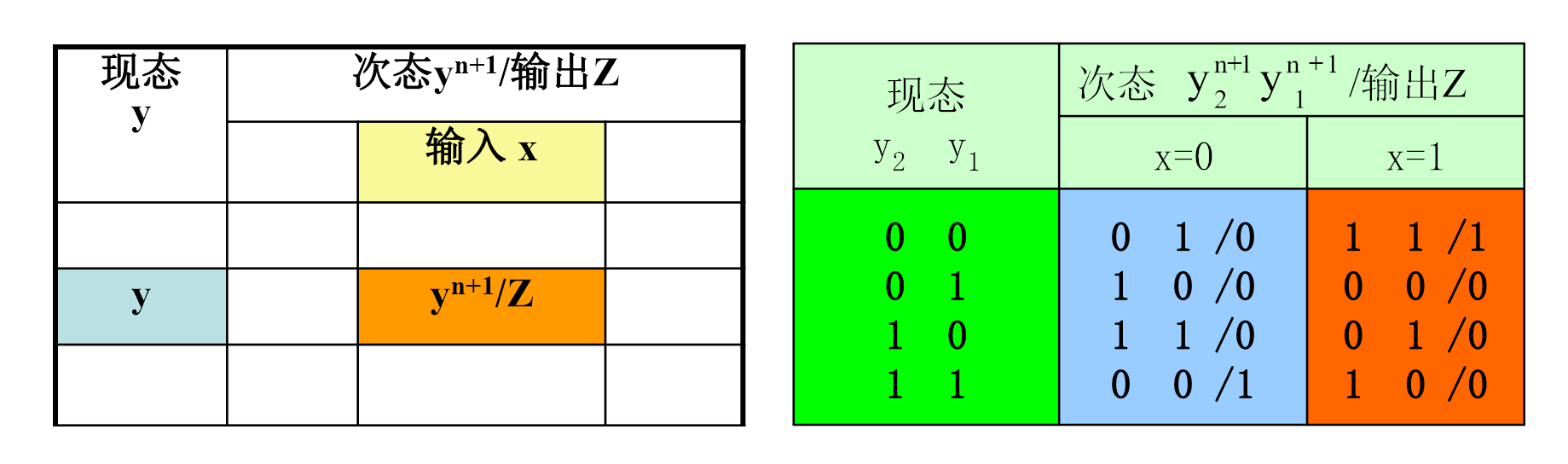
注意,Mealy型Z是和x写在一起的,因为Mealy型的输出依赖于x而Moore型没有.所以Moore型Z是单列的如下图所示.
状态图
电路状态转换规律及相应输入、输出取值关系的有向图。
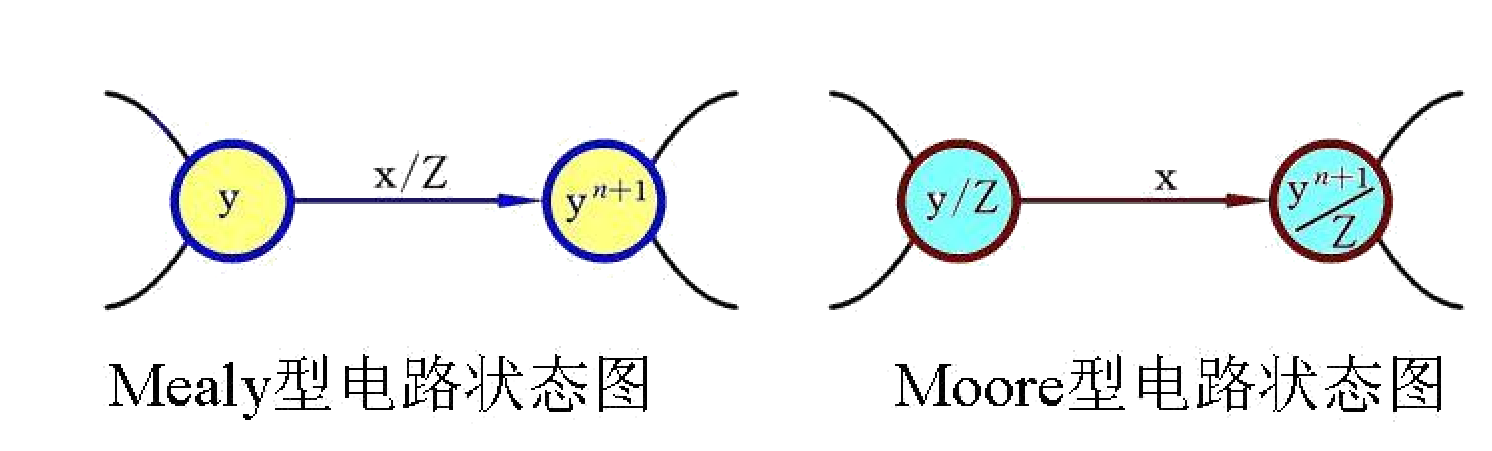
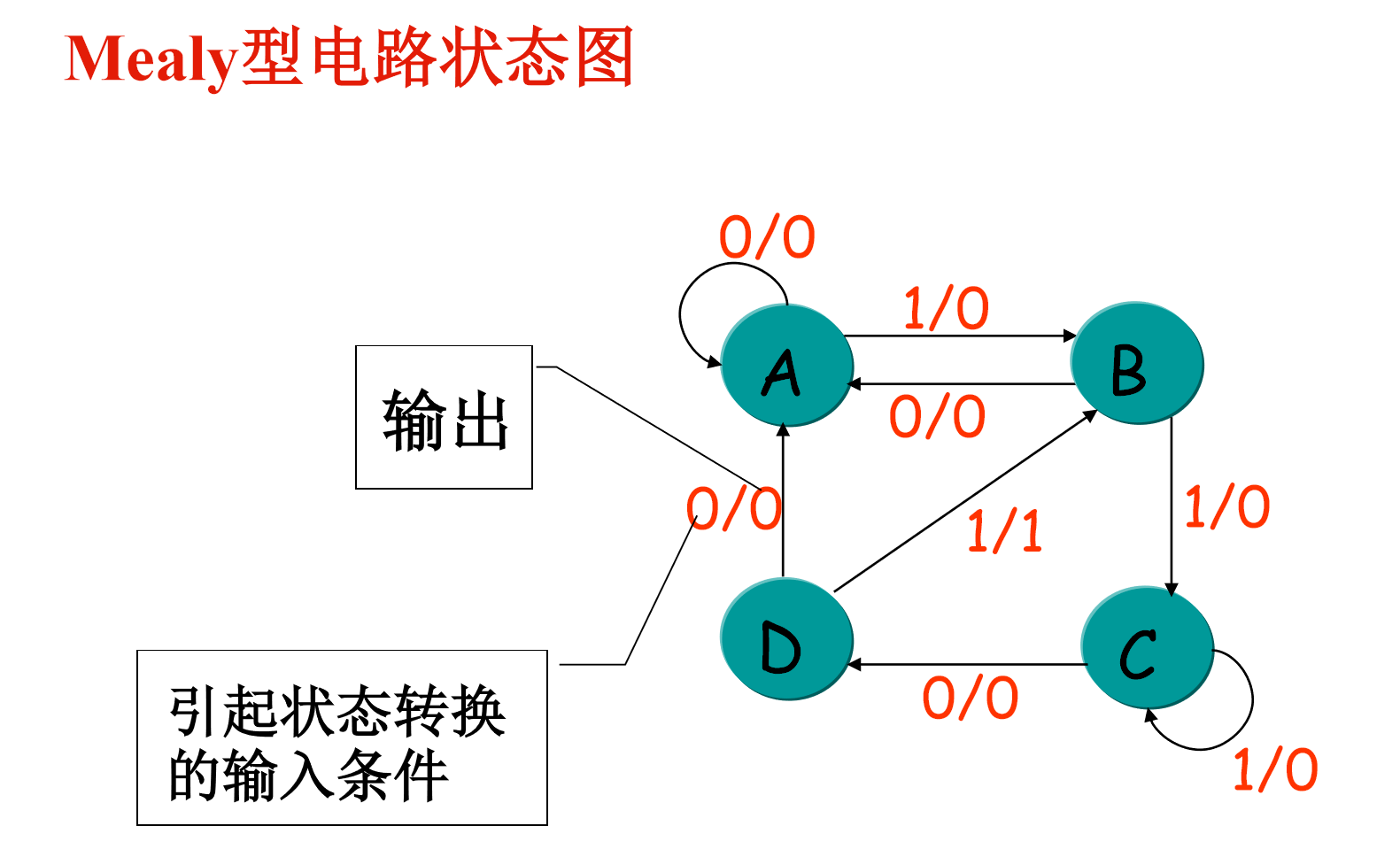
节点是触发器的工作状态,连线是总输入/总输出
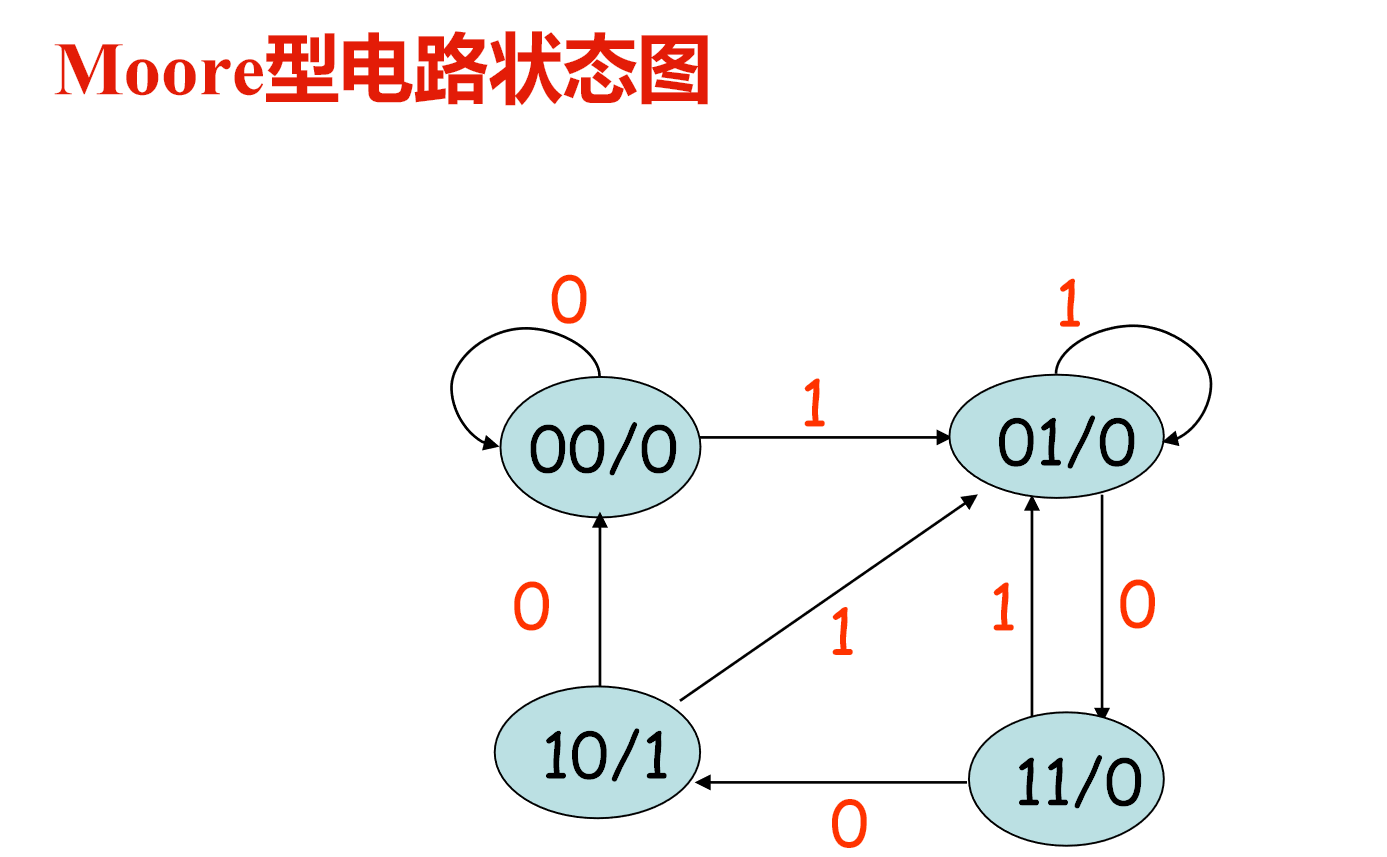
节点是触发器状态y/输出z,路径是输入x.
波形图
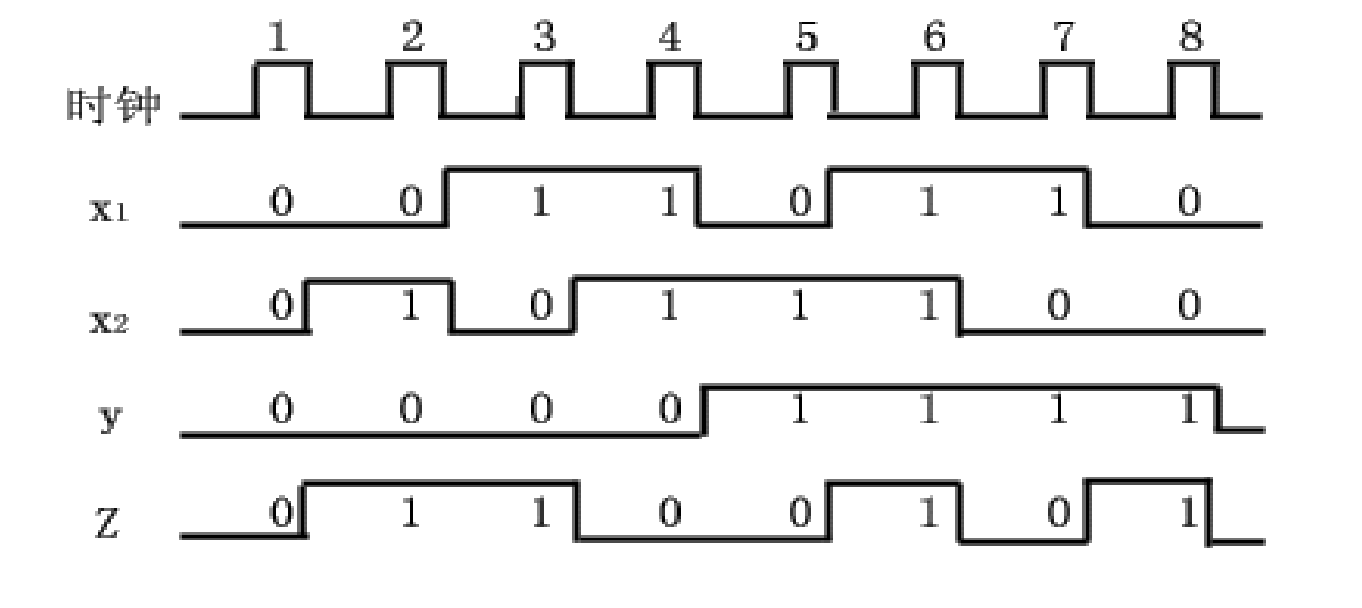
同步时序逻辑电路的分析
关键:找出电路状态和输出随输入变化而变化的规律
常用的方法:表格法、代数法
表格法
- 写出输出函数(Z=f(x,y))和激励函数(D=g(x,y))
- 借助触发器功能表列出电路次态真值表(触发器的输入-输出关系)
- 作出状态表和状态图(画出时间图)
- 归纳出电路的逻辑功能
(最好先确定电路类型)
Example
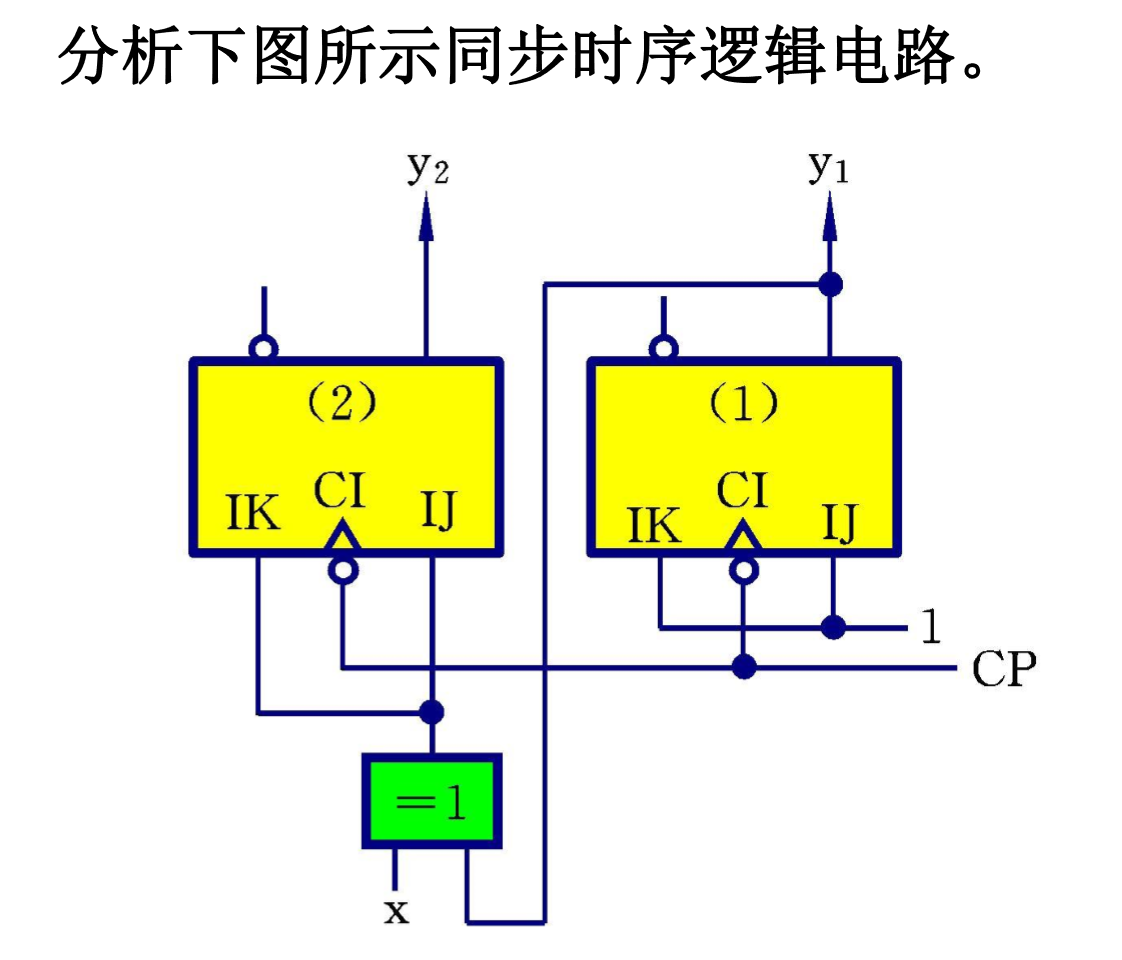
- 输出函数Z1=y1,Z2=y2,是Moore型电路
- 激励函数IK1=IJ1=1;IK2=IJ2=y1 plus x
- 次态真值表
| 输入 | y1y2 | J2K2 | J1K1 | Statements | 次态y1’y2’ |
|---|---|---|---|---|---|
| 0 | 00 | 00 | 11 | Reverse1,Keep2 | 10 |
| 0 | 01 | 00 | 11 | Reverse1,Keep2 | 11 |
| 0 | 11 | 11 | 11 | Reverse1,Reverse2 | 00 |
| 0 | 10 | 11 | 11 | Reverse1,Reverse2 | 01 |
| 1 | 00 | 11 | 11 | Reverse1,Reverse2 | 11 |
| 1 | 01 | 11 | 11 | Reverse1,Reverse2 | 10 |
| 1 | 11 | 00 | 11 | Reverse1,Keep2 | 01 |
| 1 | 10 | 00 | 11 | Reverse1,Keep2 | 00 |
- 状态图
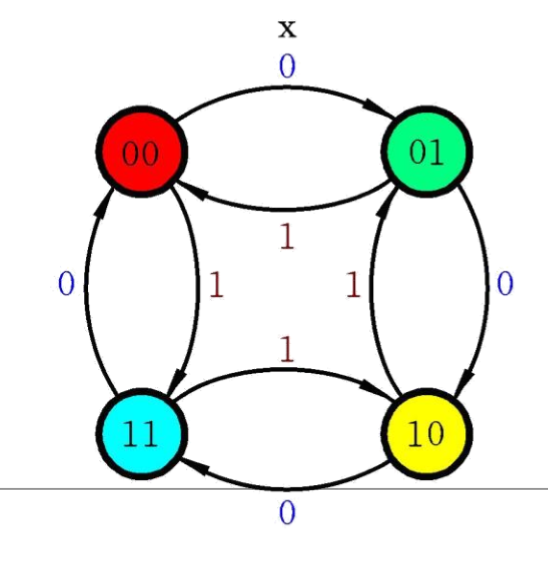
- 功能确认:该电路是一个2位二进制数可逆计数器.
- 输入为0时正向计数,为1时反向计数.
作时序图的一般步骤
- 假设电路初始状态,并拟定一典型输入序列
- 作出状态和输出响应序列
- 根据响应序列画出波形图。
代数法
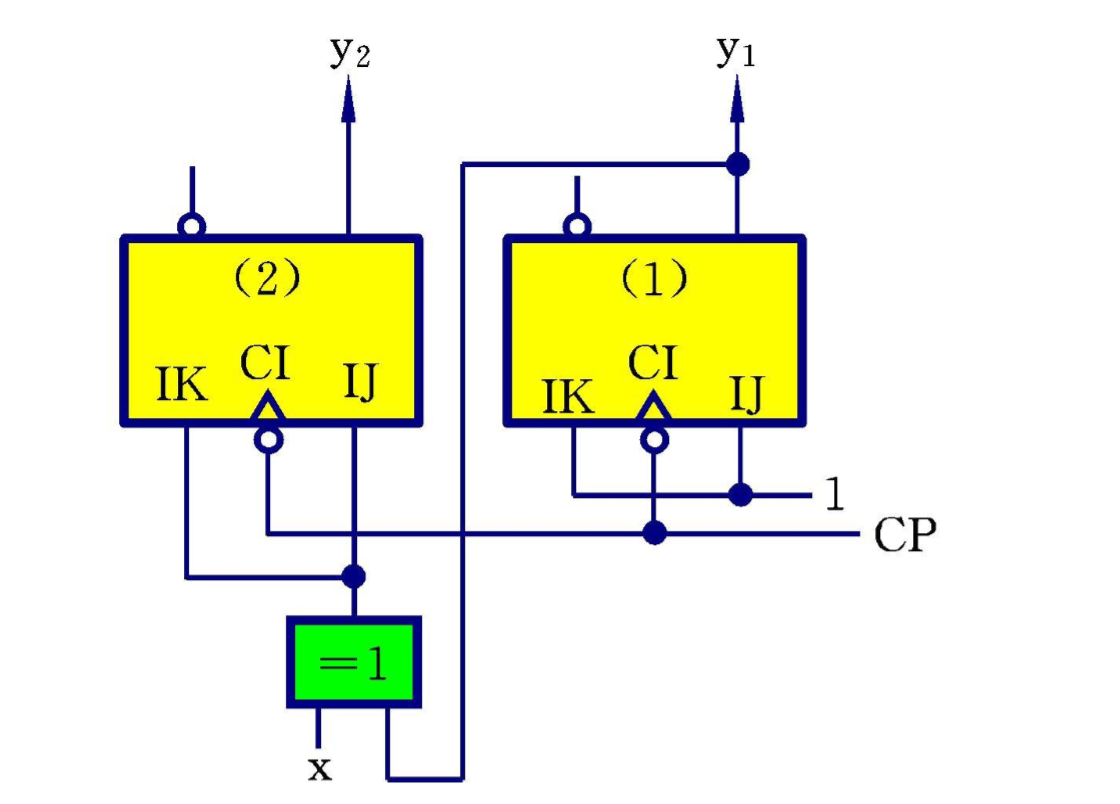
- 输出函数Z=f(y)和激励表达式K1=J1=1,K2=J2=x plus y1
- 把激励函数代入触发器次态方程,导出电路的次态方程组: y 1 ′ = g ( x , y 1 ) , y 2 ′ = h ( x , y 1 ) y'_1=g(x,y_1),y'_2=h(x,y_1) y1′=g(x,y1),y2′=h(x,y1)
- 状态表和状态图
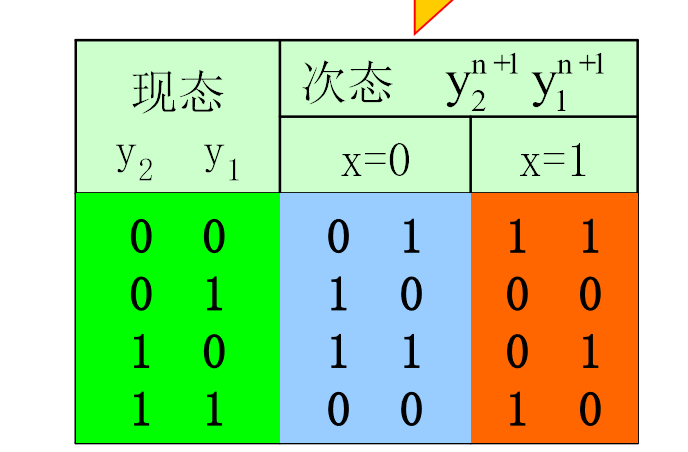
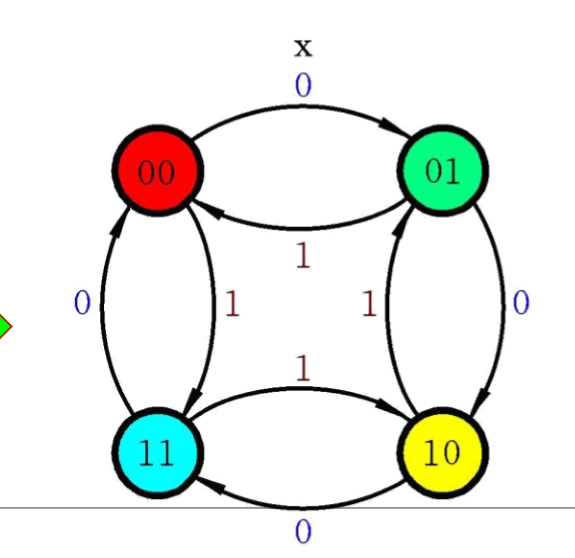
- 分析电路功能同上.
两种方法的区别在于是否通过电路分析和枚举得出次态表.相对而言,表格法的次态表更加复杂.
Conclusion
同步时序电路是组合逻辑电路和存储电路的组合,输入/输出关系复杂,在分析过程中最好分步进行.用代数法化简次态式时要运用之前的几种化简定理.
化简的简略流程如下:
| 表格法 | 确定输出函数(存储->输出)和激励函数(输入->激励) | 次态真值表(输入->输出) | 状态图(状态转移) | 归纳逻辑功能 |
| 代数法 | 确定输出函数(存储->输出)和激励函数(输入->激励) | 导出次态方程组 y ′ = f ( I n p u t , y ) y'=f(Input,y) y′=f(Input,y) | 归纳逻辑功能 |
https://www.wikiwand.com/zh-hans/%E6%97%B6%E5%BA%8F%E9%80%BB%E8%BE%91%E7%94%B5%E8%B7%AF#/%E5%90%8C%E6%AD%A5%E6%97%B6%E5%BA%8F%E9%80%BB%E8%BE%91%E7%94%B5%E8%B7%AF ↩︎
最后
以上就是善良小丸子最近收集整理的关于同步时序电路分析的全部内容,更多相关同步时序电路分析内容请搜索靠谱客的其他文章。








发表评论 取消回复