在
Forward Star:学习笔记:二极管与逻辑电路zhuanlan.zhihu.com一文中,我们讲到了与非、或非等几种逻辑门。但是它们的运作都需要输入端持续输入信号,一旦中止,信息就会丢失。
时序电路(Sequential Circuits)就旨在解决这一问题,它能够储存信息;同样地,它也有几种基本的结构。
SR Latch
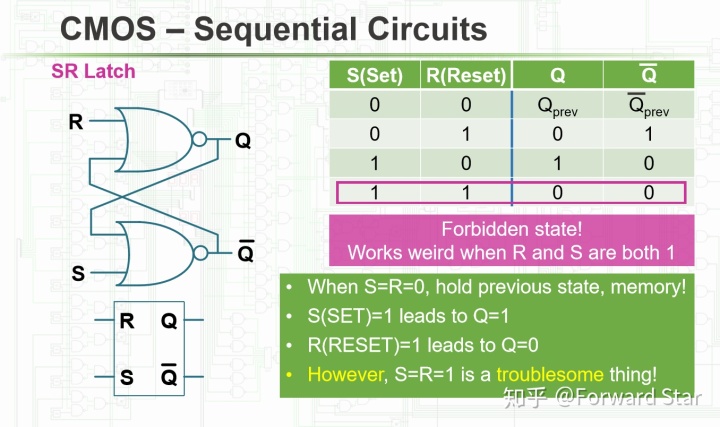
光看这个图是很令人困惑的,因为尽管两个或非门中,R、S的输入给定,但是另外一个输入端却是需要从结果推过来。如果把右边那个表直接代进去,可以发现这确实成立;然而,究竟为什么会这样呢?我们可以对电路动态地分析。如果一次只能转变
假设初始时
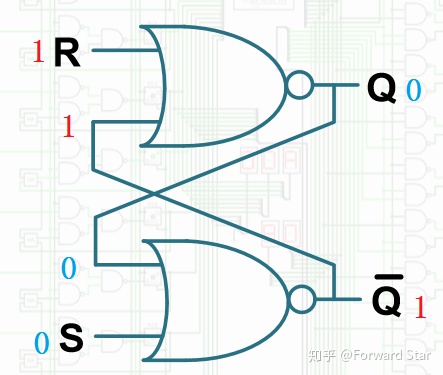
当我们把
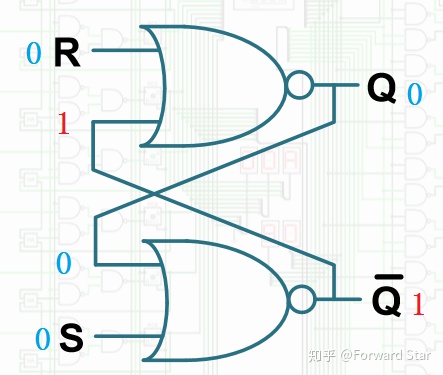
而
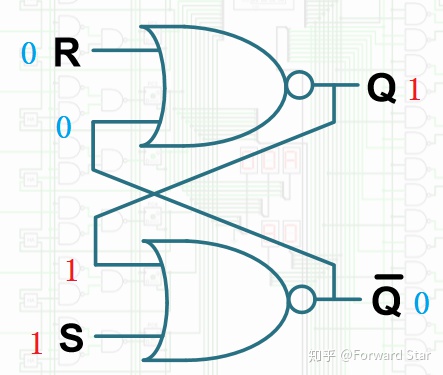
因此便有了右边那个对应的表,当
SR Latch在电路中的符号如下图:
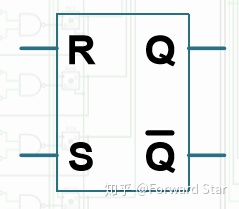
D Latch
D Latch在SR Latch的基础上改造而成。首先用一个非门把D转换为S、R:
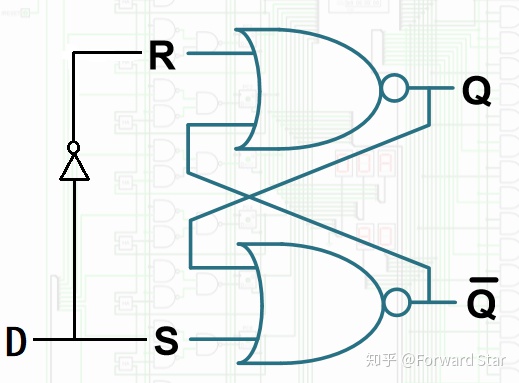
然后再接上一个CLK接口和两个与门:
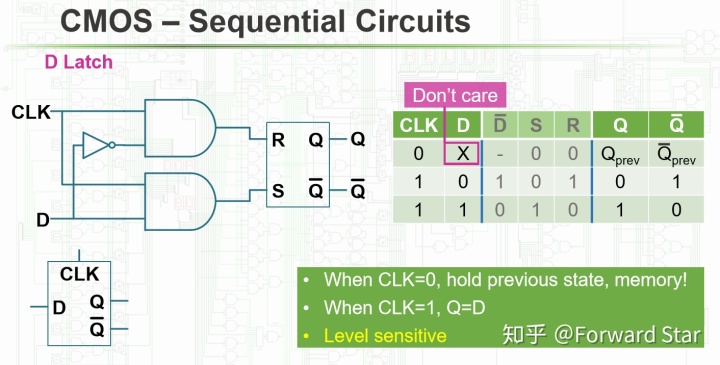
这样CLK就决定了其是否工作,如果CLK为0,两个与门的结果为0,那么R、S为0,根据SR Latch,
D Flip-Flop
尽管Latch实现了存储信息的功能,但是信号的传输有延时,这是因为非门转化器无法与D的另一端同步:
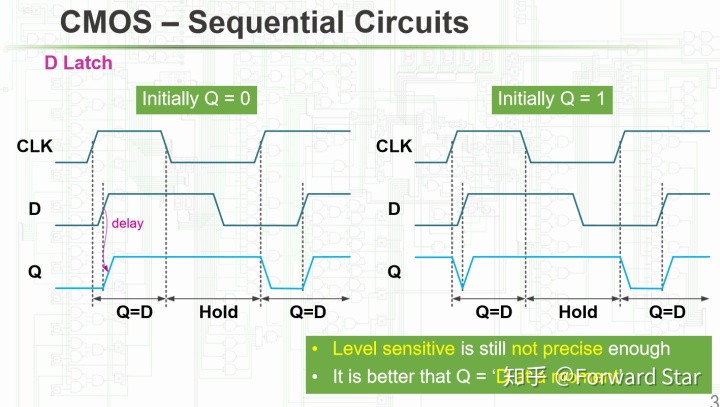
D Flip-Flop的想法是用两个D Latch,其中一个用于同步D的值,另一个决定这个值是否传给Q:
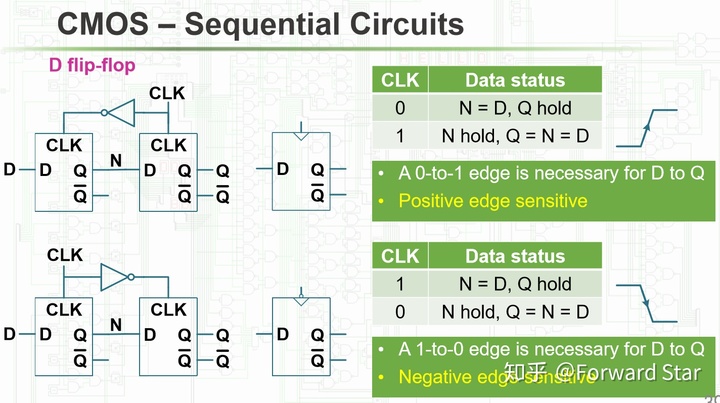
这样CLK就并非与之前一样,0是储存,1是同步;而是当CLK从0变为1或从1变为0时进行刷新。以上图第一个结构为例,当CLK从0变为1时,右边D Latch的CLK输入端瞬时改变,使Q与N同步;而左边D Latch因非门影响,短暂地维持了1的状态,即D与N仍然同步。因此,此时Q、N、D保持一致,实现刷新:
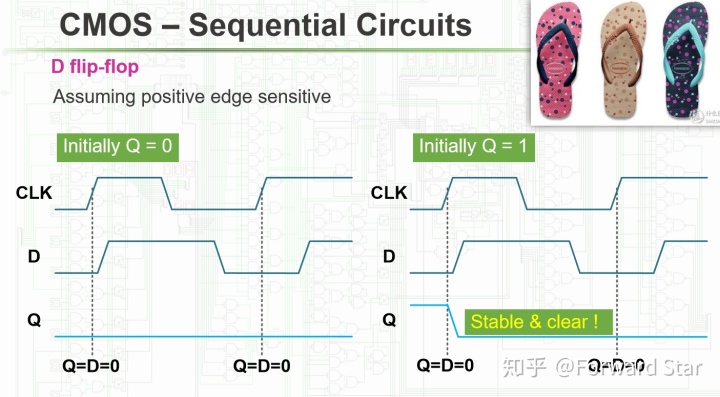
Register
Register将多个D Flip-Flop连在同一个CLK上,由于每个D Flip-Flop可传递一个二进制位,因此Register可以表示二进制数:
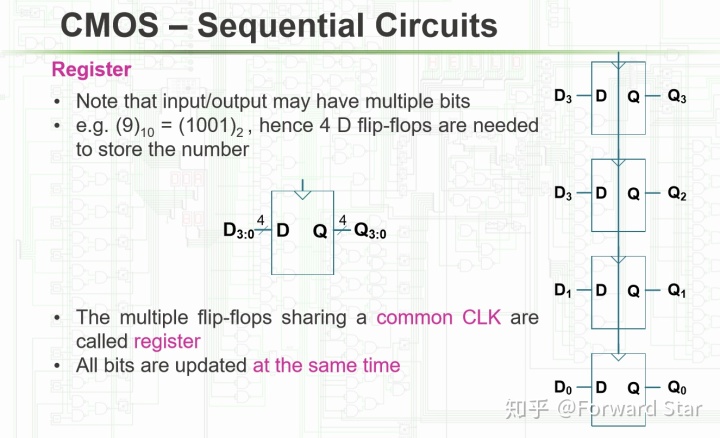
将组合电路与Register结合,可以同时实现逻辑运算和数据储存,其中组合电路用于逻辑运算,Register用于存储。
同步时序电路
给所有Register接上相同的CLK信号:
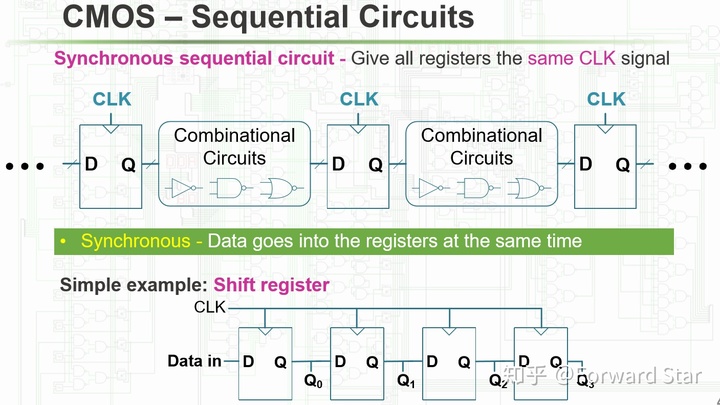
由于Register之间的逻辑运算需要时间,我们给CLK接上周期性的信号,就可以让信息传递和逻辑运算交替进行。
如果我们把一个任务拆成多个逻辑运算的部分,使得它们能并行计算,就可以提高计算的效率:
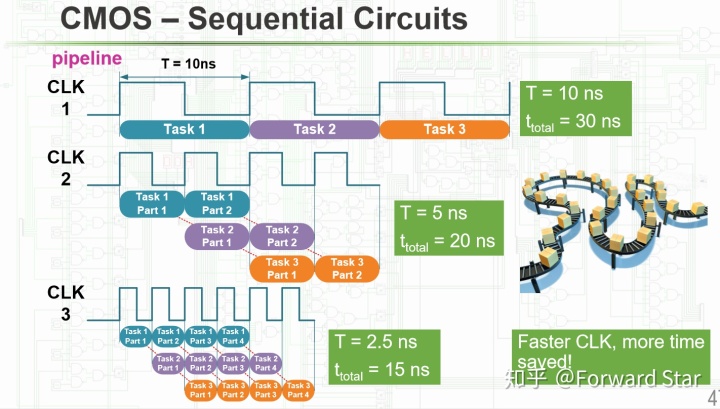
不过这也要求CLK的频率更高,因此任务不可能无限拆分。
例题
现在有一个二进制序列,每次操作你可以选择一个子序列,将子序列所有数右移一位,即
注意一个序列
分析:我们先分析题目,显然可以发现每次子序列必须是01交替出现,即01010或10101;如果中间有连续的0或1,那么右移的时候连续的一段其实和不移的效果是一样的。那么问题就转化为最少可以把原序列分成多少个01序列。这样我们只需要看最长的一段1与最长一段0中长度的最大值即可。
我们构造:
即最大/最小连续子序列和.
考虑动态规划,inputs是序列中当前的数
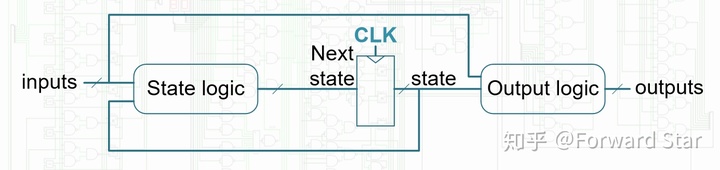
最后
以上就是踏实大碗最近收集整理的关于以下不属于时序逻辑电路的有_学习笔记:时序电路基础的全部内容,更多相关以下不属于时序逻辑电路内容请搜索靠谱客的其他文章。








发表评论 取消回复