文章目录
- 1.题目一
- 2.题目二
- 3.题目三
- 4.题目四
- 5.题目五
- 6.题目六
1.题目一
已知一个IIR系统的传递函数为
将其从直接型转换为级联型、并联型和格型结构,并画出各种结构的信号流图。
级联型:

由sos和g的数据可列出级联型的表达式:
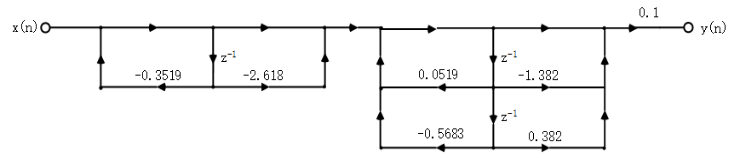
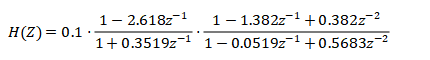 对应的级联型结构的信号流图如下:
对应的级联型结构的信号流图如下:
并联型:

由A、B、C的数据,可以列出并联型的表达式为:
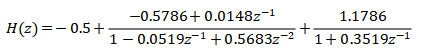
对应的并联型结构的信号流图如下:
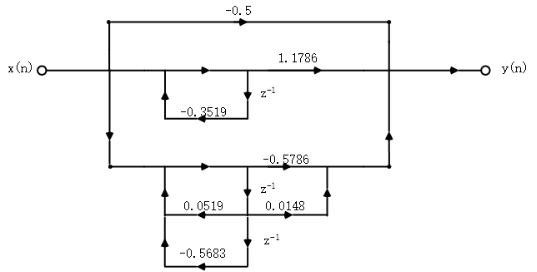
格型:

由K、C1的数据,可画出对应的格型结构的信号流图如下:

function [C,B,A] = dir2par(num,den)
%进行直接型到并联型的转换
% 此处显示详细说明
M=length(num);N=length(den);
[r,p,C]=residuez(num,den);%先求系统的单根p1,对应的留数r1及直接项C
%变换为二阶子系统
K=floor(N/2);B=zeros(K,2);A=zeros(K,3);%二阶子系统变量的初始化
if K*2==N %N为偶数,A(z)的次数为奇,有一个因式是一阶的
for i=1:2:N-2
Brow=r(i:1:i+1,:);%取出一对留数
Arow=p(i:1:i+1,:);%取出一对对应的极点
%二个留数极点转为二阶子系统分子分母系数
[Brow,Arow]=residuez(Brow,Arow,[]);
B(fix((i+1)/2),:)=real(Brow);
A(fix((i+1)/2),:)=real(Arow);
end
[Brow,Arow]=residuez(r(N-1),p(N-1),[]);
B(K,:)=[real(Brow),0];A(K,:)=[real(Arow),0];
else
for i=1:2:N-2
Brow=r(i:1:i+1,:);%取出一对留数
Arow=p(i:1:i+1,:);%取出一对对应的极点
%二个留数极点转为二阶子系统分子分母系数
[Brow,Arow]=residuez(Brow,Arow,[]);
B(fix((i+1)/2),:)=real(Brow);
A(fix((i+1)/2),:)=real(Arow);
end
end
end
%question 1
clear;
b=[0.1,-0.4,0.4,-0.1];%输入系统函数b参数
a=[1,0.3,0.55,0.2];%输入系统函数a参数
[sos,g]=tf2sos(b,a) %由直接型转换到级联型
[C,B,A]=dir2par(b,a) %由直接型转换为并联型
[K,C1]=tf2latc(b,a) %由直接型转换为格型
2.题目二
2.已知一个FIR系统的传递函数为
将其从横截型转换为级联型和格型结构,并画出各种结构的信号流图。
级联型:

由sos和g的数据可以列出级联型的表达式为:
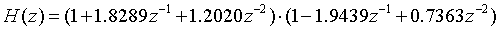
对应的级联型结构的信号流图为:
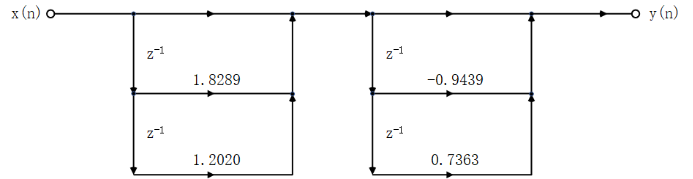
格型:

由K的数据可以画出对应的格型结构的信号流图为:
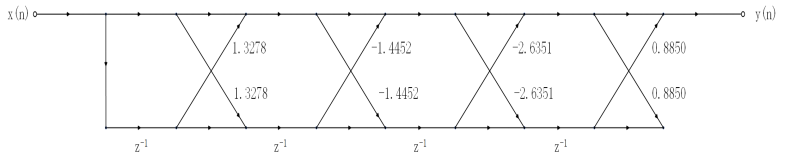
该结构图为全零点FIR系统的格型结构图。
%question 2
clear;
b=[1,0.885,0.212,0.212,0.885];%输入系统函数b参数
a=1;%输入系统函数a参数
[sos,g]=tf2sos(b,a) %由直接型转换为级联型
K=tf2latc(b,1) %由直接型转换为格型
3.题目三
3.三个IIR滤波器的方程和系统函数分别为:
编制MATLAB程序,求出各滤波器的级联型网格的系数,并画出级联结构;
编制MATLAB程序,求出各滤波器的并联型网格的系数,并画出并联结构。
对第一个IIR滤波器:
级联型:
由sos1和g1的数据可列出级联型的表达式为:
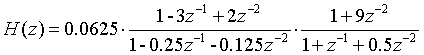
对应的级联型结构的信号流图为:

并联型:

由C1、B1、A1的数据可列出并联型的表达式为:
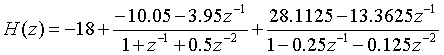
对应的并联型结构的信号流图为:
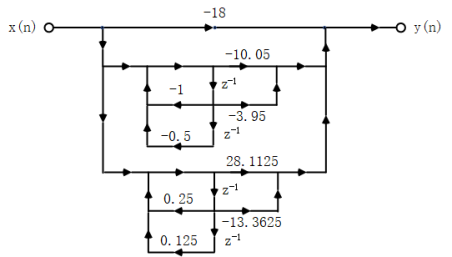
对第二个IIR滤波器:
级联型:

由sos2和g2可列出级联型的表达式为:
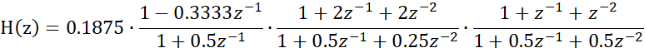
对应的级联型结构的信号流图为:

并联型:

由C2、B2、A2的数据可列出并联型的表达式为:
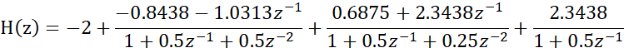
对应的并联型结构的信号流图如下:
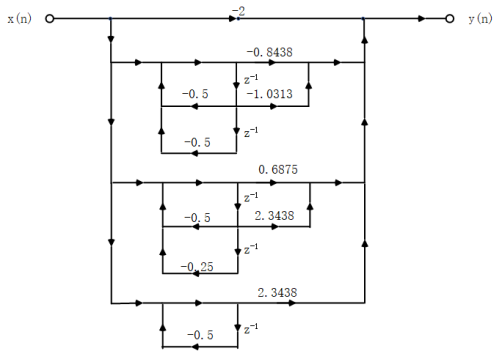
对第三个IIR滤波器:
级联型:

由sos3和g3可列出级联型的表达式为:
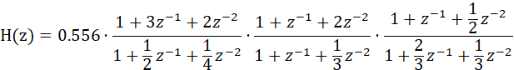
对应的级联型结构的信号流图为:

并联型:

由C3、B3、A3的数据可列出并联型的表达式为:
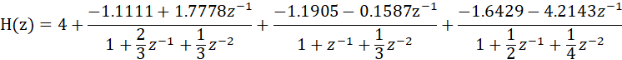
对应的并联型结构的信号流图如下:
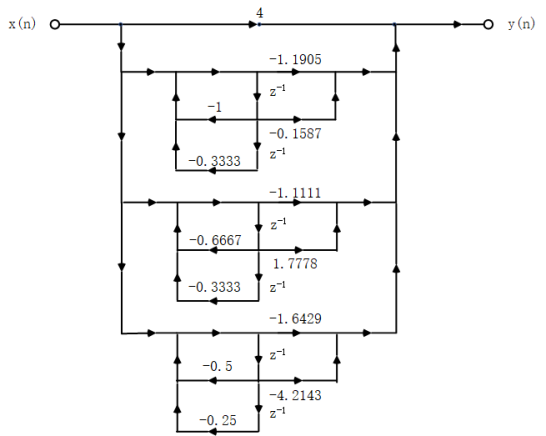
%question 3
clear;
b1=[1,-3,11,-27,18];
a1=[16,12,2,-4,-1];
[sos1,g1]=tf2sos(b1,a1) %由直接型转换到级联型
[C1,B1,A1]=dir2par(b1,a1) %由直接型转换为并联型
b2=[3,8,12,7,2,-2];
a2=[16,24,24,14,5,1];
[sos2,g2]=tf2sos(b2,a2) %由直接型转换到级联型
[C2,B2,A2]=dir2par(b2,a2) %由直接型转换为并联型
b3=[2,10,23,34,31,16,4];
a3=[36,78,87,59,26,7,1];
[sos3,g3]=tf2sos(b3,a3) %由直接型转换到级联型
[C3,B3,A3]=dir2par(b3,a3) %由直接型转换为并联型
4.题目四
设计一个模拟原型低通滤波器,通带截止频率fp=6kHz,通带最大衰减Rp≤1dB,阻带截止频率fs=15kHz,阻带最小衰减As≥30dB。要求:分别实现符合以上指标的巴特沃斯滤波器、切比雪夫I型滤波器、切比雪夫丌型滤波器和椭圆滤波器,绘制幅频特性曲线和相频特性曲线、零极点分布图,并列写出传递函数表示式。
使用MATLAB进行求解:
巴特沃斯滤波器:
使用MATLAB工具箱函数buttord计算滤波器的阶数和3dB截止频率,再使用buttap函数由巴特沃斯滤波器原型设计相应的滤波器。
得到的幅频特性曲线、相频特性曲线、零极点分布图如下:
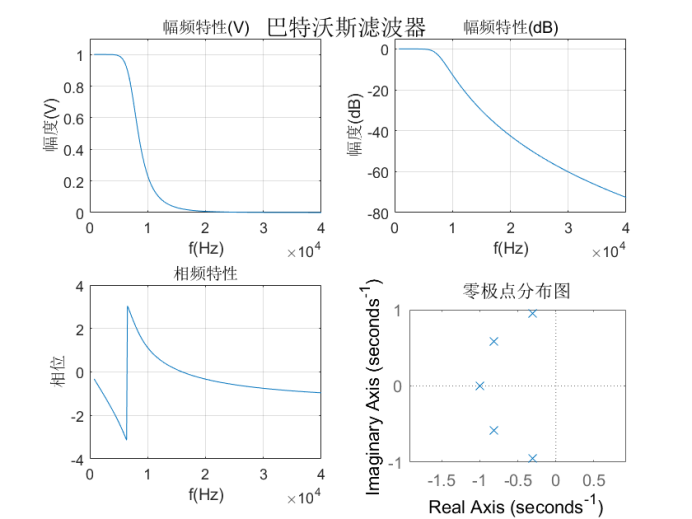
将滤波器系数a和b按多项式的形式展示:

即相应的传递函数表达式为:
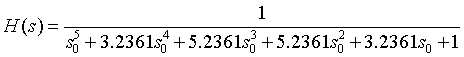
切比雪夫I型滤波器:
使用MATLAB工具箱函数cheb1ord计算滤波器的阶数和3dB截止频率,再使用cheb1ap函数由切比雪夫I型滤波器原型设计相应的滤波器。
得到的幅频特性曲线、相频特性曲线、零极点分布图如下:
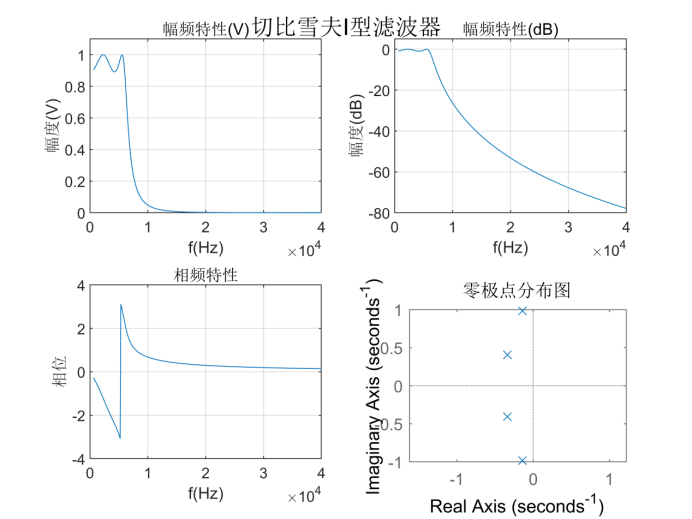
将滤波器系数a和b按多项式的形式展示:

即相应的传递函数表达式为:
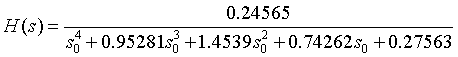
切比雪夫II型滤波器:
使用MATLAB工具箱函数cheb2ord计算滤波器的阶数和3dB截止频率,再使用cheb2ap函数由切比雪夫II型滤波器原型设计相应的滤波器。
得到的幅频特性曲线、相频特性曲线、零极点分布图如下:
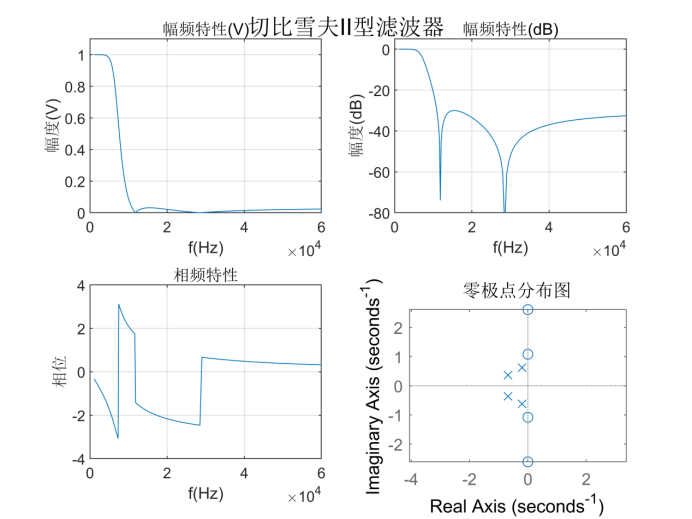
将滤波器系数a和b按多项式的形式展示:

即相应的传递函数表达式为:
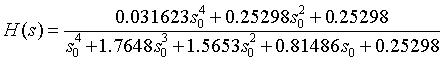
椭圆滤波器:
使用MATLAB工具箱函数ellipord计算滤波器的阶数和3dB截止频率,再使用ellipap函数由切比雪夫II型滤波器原型设计相应的滤波器。
得到的幅频特性曲线、相频特性曲线、零极点分布图如下:
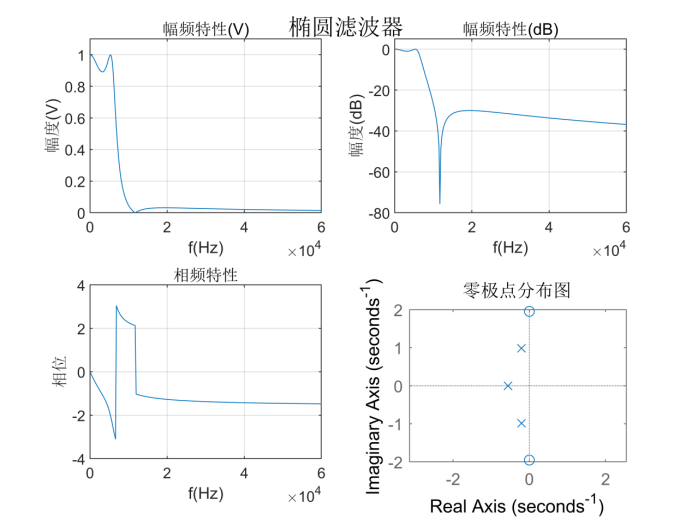
将滤波器系数a和b按多项式的形式展示:

即相应的传递函数表达式为:
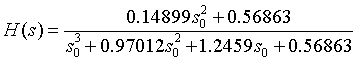
%question 4
clear;
fp=6000;Omgp=2*pi*fp; %输入滤波器的通带截止频率
fs=15000;Omgs=2*pi*fs; %输入滤波器的阻带截止频率
Rp=1;As=30; %输入滤波器的通阻带衰减指标
%巴特沃斯滤波器
[n,Omgc]=buttord(Omgp,Omgs,Rp,As,'s');%计算模拟滤波器阶数和3dB截止频率
[z0,p0,k0]=buttap(n);
b0=k0*real(poly(z0)); %求滤波器系数b0
a0=real(poly(p0)); %求滤波器系数a0
[H,Omg]=freqs(b0,a0); %求系统的频率响应
dbH=20*log10((abs(H)+eps)/max(abs(H)));%求分贝值,加eps避开0点
buttPa=poly2str(a0,'s')
buttPb=poly2str(b0,'s')
figure;suptitle('巴特沃斯滤波器')
subplot(2,2,1);plot(Omg*Omgc/2/pi,abs(H));
grid on;box on;title('幅频特性(V)');
axis([0,40000,0,1.1]);xlabel('f(Hz)');ylabel('幅度(V)');
subplot(2,2,2);plot(Omg*Omgc/2/pi,dbH);
grid on;box on;title('幅频特性(dB)');
axis([0,40000,-80,5]);xlabel('f(Hz)');ylabel('幅度(dB)');
subplot(2,2,3);plot(Omg*Omgc/2/pi,angle(H));
grid on;box on;title('相频特性');
axis([0,40000,-4,4]);xlabel('f(Hz)');ylabel('相位');
subplot(2,2,4);pzmap(b0,a0); %绘制零极点图
axis square,axis equal
title('零极点分布图')
%切比雪夫I型
[n,Omgn]=cheb1ord(Omgp,Omgs,Rp,As,'s');
[z0,p0,k0]=cheb1ap(n,Rp);
b0=k0*real(poly(z0)); %求滤波器系数b0
a0=real(poly(p0)); %求滤波器系数a0
b1=[zeros(1,length(a0)-length(b0)),b0];%将b0左端补0.使其与a0等长
[H,Omg]=freqs(b0,a0); %求系统的频率响应
dbH=20*log10((abs(H)+eps)/max(abs(H)));
cheb1Pa=poly2str(a0,'s')
cheb1Pb=poly2str(b0,'s')
figure;suptitle('切比雪夫I型滤波器')
subplot(2,2,1);plot(Omg*Omgn/2/pi,abs(H));
grid on;box on;title('幅频特性(V)');
axis([0,40000,0,1.1]);xlabel('f(Hz)');ylabel('幅度(V)');
subplot(2,2,2);plot(Omg*Omgn/2/pi,dbH);
grid on;box on;title('幅频特性(dB)');
axis([0,40000,-80,5]);xlabel('f(Hz)');ylabel('幅度(dB)');
subplot(2,2,3);plot(Omg*Omgn/2/pi,angle(H));
grid on;box on;title('相频特性');
axis([0,40000,-4,4]);xlabel('f(Hz)');ylabel('相位');
subplot(2,2,4);pzmap(b0,a0); %绘制零极点图
axis square,axis equal
title('零极点分布图')
%切比雪夫II型
[n,Omgn]=cheb2ord(Omgp,Omgs,Rp,As,'s');
[z0,p0,k0]=cheb2ap(n,As);
b0=k0*real(poly(z0)); %求滤波器系数b0
a0=real(poly(p0)); %求滤波器系数a0
b1=[zeros(1,length(a0)-length(b0)),b0];%将b0左端补0.使其与a0等长
[H,Omg]=freqs(b0,a0); %求系统的频率响应
dbH=20*log10((abs(H)+eps)/max(abs(H)));
cheb2Pa=poly2str(a0,'s')
cheb2Pb=poly2str(b0,'s')
figure;suptitle('切比雪夫II型滤波器')
subplot(2,2,1);plot(Omg*Omgn/2/pi,abs(H));
grid on;box on;title('幅频特性(V)');
axis([0,60000,0,1.1]);xlabel('f(Hz)');ylabel('幅度(V)');
subplot(2,2,2);plot(Omg*Omgn/2/pi,dbH);
grid on;box on;title('幅频特性(dB)');
axis([0,60000,-80,5]);xlabel('f(Hz)');ylabel('幅度(dB)');
subplot(2,2,3);plot(Omg*Omgn/2/pi,angle(H));
grid on;box on;title('相频特性');
axis([0,60000,-4,4]);xlabel('f(Hz)');ylabel('相位');
subplot(2,2,4);pzmap(b0,a0); %绘制零极点图
axis square,axis equal
title('零极点分布图')
%椭圆滤波器
[n,Omgn]=ellipord(Omgp,Omgs,Rp,As,'s');
[z0,p0,k0]=ellipap(n,Rp,As);
b0=k0*real(poly(z0)); %求滤波器系数b0
a0=real(poly(p0)); %求滤波器系数a0
b1=[zeros(1,length(a0)-length(b0)),b0];%将b0左端补0.使其与a0等长
[H,Omg]=freqs(b0,a0); %求系统的频率响应
dbH=20*log10((abs(H)+eps)/max(abs(H)));
ellip2Pa=poly2str(a0,'s')
ellip2Pb=poly2str(b0,'s')
figure;suptitle('椭圆滤波器')
subplot(2,2,1);plot(Omg*Omgn/2/pi,abs(H));
grid on;box on;title('幅频特性(V)');
axis([0,60000,0,1.1]);xlabel('f(Hz)');ylabel('幅度(V)');
subplot(2,2,2);plot(Omg*Omgn/2/pi,dbH);
grid on;box on;title('幅频特性(dB)');
axis([0,60000,-80,5]);xlabel('f(Hz)');ylabel('幅度(dB)');
subplot(2,2,3);plot(Omg*Omgn/2/pi,angle(H));
grid on;box on;title('相频特性');
axis([0,60000,-4,4]);xlabel('f(Hz)');ylabel('相位');
subplot(2,2,4);pzmap(b0,a0); %绘制零极点图
axis square,axis equal
title('零极点分布图')
5.题目五
5.用频率变换法设计一个切比雪夫I型模拟低通滤波器,要求通带截止频率fp= 3.5kHz,通带最大衰减Rp≤1dB,阻带截止频率fs = 6kHz,阻带最小衰减As≥40dB。绘制归一化的模拟滤波器原型和实际的模拟低通滤波器的频率特性。
使用MATLAB进行求解:
使用cheb1ord函数求出滤波器的阶数和3dB截止频率,再通过cheb1ap计算模拟滤波器的低通原型,得到归一化的模拟滤波器原型,再通过lp2lp从归一化低通变换到实际低通,求得实际的模拟低通滤波器的频率特性。
归一化的模拟滤波器原型和实际的模拟低通滤波器的频率特性如下:
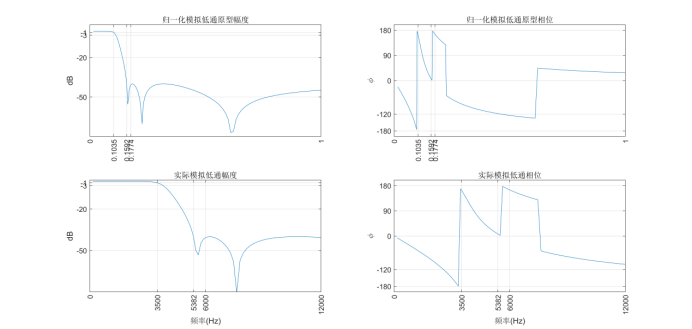
由归一化低通原型滤波器的频率特性及经频率变换求得的实际滤波器频率特性可看出,归一化低通原型和实际滤波器频率特性是一致的。由频率特性曲线可知,该设计结果在通阻带截止频率处能满足Rp≤1dB、As≥40dB的设计指标要求。
%question 5
clear;
fp=3500;Omgp=2*pi*fp; %输入实际滤波器的通带截止频率
fs=6000;Omgs=2*pi*fs; %输入实际滤波器的阻带截止频率
Rp=1;As=40;
[n,Omgn]=cheb2ord(Omgp,Omgs,Rp,As,'s');%计算滤波器的阶数和3dB截止频率
[z0,p0,k0]=cheb2ap(n,As);
b0=k0*real(poly(z0)); %求归一化的滤波器系数b0
a0=real(poly(p0)); %求归一化的滤波器系数a0
[H,Omg0]=freqs(b0,a0); %求归一化的滤波器频率特性
dbH=20*log10((abs(H)+eps)/max(abs(H)));
[ba,aa]=lp2lp(b0,a0,Omgn);%从归一化低通变换到实际低通
[Ha,Omga]=freqs(ba,aa);%求实际系统的频率特性
dbHa=20*log10((abs(Ha)+eps)/max(abs(H)));
Omg0p=fp/Omgn; %通带截止频率归一化
Omg0c=Omgn/2/pi/Omgn; %3dB截止频率归一化
Omg0s=fs/Omgn; %阻带截止频率归一化
fc=floor(Omgn/2/pi); %3dB截止频率
%归一化模拟低通原型频率特性作图
subplot(2,2,1),plot(Omg0/2/pi,dbH);
title('归一化模拟低通原型幅度');
ylabel('dB');grid on;axis([0,1,-80,5])
set(gca,'Xtick',[0,Omg0p,Omg0c,Omg0s,1]);
set(gca,'XtickLabelRotation',90);
set(gca,'Ytick',[-50,-20,-3,-1]);
subplot(2,2,2),plot(Omg0/2/pi,angle(H)/pi*180);
title('归一化模拟低通原型相位');
ylabel('phi');grid on;axis([0,1,-200,200])
set(gca,'Xtick',[0,Omg0p,Omg0c,Omg0s,1]);
set(gca,'XtickLabelRotation',90);
set(gca,'Ytick',[-180,-120,0,90,180]);
%实际模拟低通频率特性作图
subplot(2,2,3),plot(Omga/2/pi,dbHa);
title('实际模拟低通幅度');xlabel('频率(Hz)')
ylabel('dB');grid on;axis([0,2*fs,-80,1])
set(gca,'Xtick',[0,fp,fc,fs,2*fs]);
set(gca,'XtickLabelRotation',90);
set(gca,'Ytick',[-50,-20,-3,-1]);
subplot(2,2,4),plot(Omga/2/pi,angle(Ha)/pi*180);
title('实际模拟低通相位');xlabel('频率(Hz)')
ylabel('phi');grid on;axis([0,2*fs,-200,200])
set(gca,'Xtick',[0,fp,fc,fs,2*fs]);
set(gca,'XtickLabelRotation',90);
set(gca,'Ytick',[-180,-120,0,90,180]);
6.题目六
用频率变换法设计一个椭圆模拟带通滤波器,要求通带截止频率fp1=3.5kHz,fp2=5.5kHz,通带最大衰减Rp≤1dB,阻带下截止频率fs1=3kHz,阻带上截止频率fs2=6kHz,阻带最小衰减As≥40dB。绘制归一化的模拟滤波器原型和实际的模拟带通滤波器的频率特性。
使用MATLAB进行求解:
使用ellipord函数求出滤波器的阶数和3dB截止频率,再通过ellipap计算模拟滤波器的低通原型,得到归一化的模拟滤波器原型,再通过lp2bp从归一化低通变换到实际带通,求得实际的模拟带通滤波器的频率特性。
归一化的模拟滤波器原型和实际的模拟带通滤波器的频率特性如下:
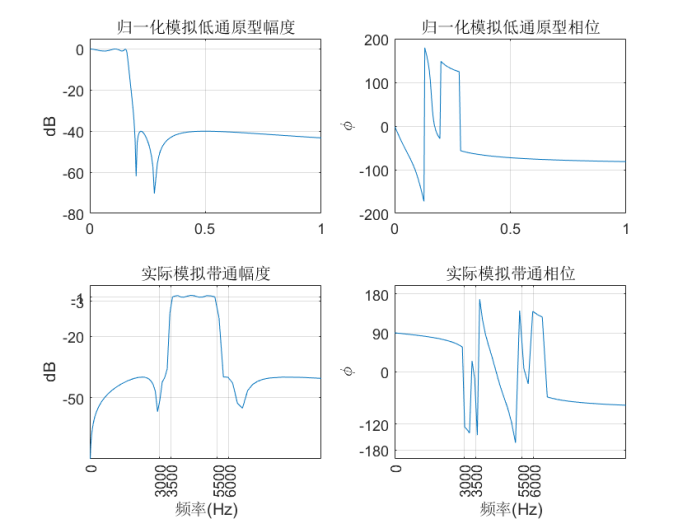
由归一化低通原型滤波器的频率特性和经频率变换求得的模拟带通滤波器频率特性可以看出,模拟带通滤波器频率特性是将低通频率特性关于中心频率对称构成。该设计结果在通阻带截止频率处能满足Rp≤1dB、As≥40dB的设计指标要求。
%question 6
clear;
clear;
fp1=3500;Op1=2*pi*fp1; %输入带通滤波器的通带截止频率
fp2=5500;Op2=2*pi*fp2;
Omgp=[Op1,Op2];
fs1=3000;Os1=2*pi*fs1; %输入带通滤波器的阻带截止频率
fs2=6000;Os2=2*pi*fs2;
Omgs=[Os1,Os2];
bw=Op2-Op1;w0=sqrt(Op1*Op2);%求通带宽度和中心频率
Rp=1;As=40; %输入滤波器的通阻带衰减指标
[n,Omgc]=ellipord(Omgp,Omgs,Rp,As,'s');%计算滤波器的阶数和3dB截止频率
[z0,p0,k0]=ellipap(n,Rp,As);
b0=k0*real(poly(z0)); %求归一化的滤波器系数b0
a0=real(poly(p0)); %求归一化的滤波器系数a0
[H,Omg0]=freqs(b0,a0); %求归一化的滤波器频率特性
dbH=20*log10((abs(H)+eps)/max(abs(H)));
[ba,aa]=lp2bp(b0,a0,w0,bw);%从归一化低通变换到模拟带通
[Ha,Omga]=freqs(ba,aa);%求实际系统的频率特性
dbHa=20*log10((abs(Ha)+eps)/max(abs(H)));
%归一化模拟低通原型频率特性作图
subplot(2,2,1),plot(Omg0/2/pi,dbH);
title('归一化模拟低通原型幅度');
ylabel('dB');grid on;axis([0,1,-80,5])
subplot(2,2,2),plot(Omg0/2/pi,angle(H)/pi*180);
title('归一化模拟低通原型相位');
ylabel('phi');grid on;axis([0,1,-200,200])
%实际模拟低通频率特性作图
subplot(2,2,3),plot(Omga/2/pi,dbHa);
title('实际模拟带通幅度');xlabel('频率(Hz)')
ylabel('dB');grid on;axis([0,10000,-80,5])
set(gca,'Xtick',[0,fs1,fp1,fp2,fs2]);
set(gca,'XtickLabelRotation',90);
set(gca,'Ytick',[-50,-20,-3,-1]);
subplot(2,2,4),plot(Omga/2/pi,angle(Ha)/pi*180);
title('实际模拟带通相位');xlabel('频率(Hz)')
ylabel('phi');grid on;axis([0,10000,-200,200])
set(gca,'Xtick',[0,fs1,fp1,fp2,fs2]);
set(gca,'XtickLabelRotation',90);
set(gca,'Ytick',[-180,-120,0,90,180]);
最后
以上就是敏感宝贝最近收集整理的关于数字信号处理实验71.题目一2.题目二3.题目三4.题目四5.题目五6.题目六的全部内容,更多相关数字信号处理实验71内容请搜索靠谱客的其他文章。
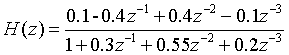
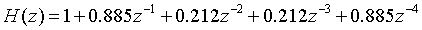
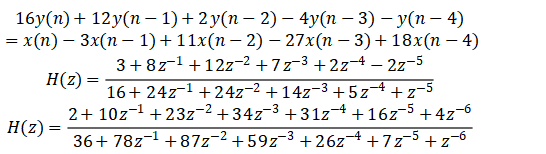








发表评论 取消回复