目录
- 1.题目一
- 2.题目二
- 3.题目三
- 4.题目四
- 5.题目五
- 6.题目六
- 7.题目七
1.题目一
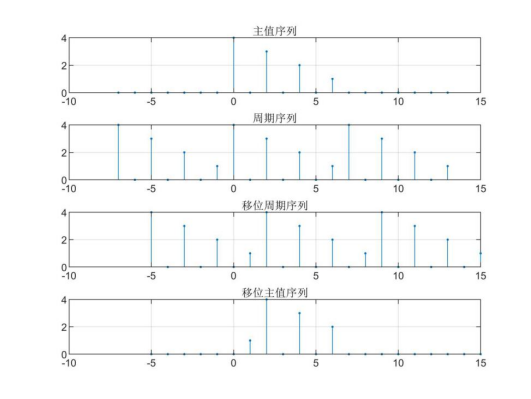
已知有限长序列x(n) = [4,0,3,0,2,0,1],求x(n)右移2位成为新的向量y(n),并画出循环移位的中间过程。(利用matlab作答)
先建立x(n)的序列,将其进行周期延拓后再进行移位操作,最后取主值序列即可得到循环移位后的序列。结果如下:
%question 1
clear;
xn=[4,0,3,0,2,0,1];%建立xn序列
Nx=length(xn);
nx=0:Nx-1;
nx1=-Nx:2*Nx-1;%设立周期延拓的范围
x1=xn(mod(nx1,Nx)+1);%建立周期延拓序列
ny1=nx1+2;y1=x1;%将x1右移2位,得到y1
RN=(nx1>=0)&(nx1<Nx);%在x1的位置向量nx1上设置主值窗
RN1=(ny1>=0)&(ny1<Nx);%在y1的位置向量ny1上设置主值窗
subplot(4,1,1),stem(nx1,RN.*x1,'.');%画出x1的主值部分
axis([-10,15,0,4]);title('主值序列');grid on
subplot(4,1,2),stem(nx1,x1,'.');%画出x1
axis([-10,15,0,4]);title('周期序列');grid on
subplot(4,1,3),stem(ny1,y1,'.');%画出y1
axis([-10,15,0,4]);title('移位周期序列');grid on
subplot(4,1,4),stem(ny1,RN1.*y1,'.');%画出y1的主值部分
axis([-10,15,0,4]);title('移位主值序列');grid on
2.题目二
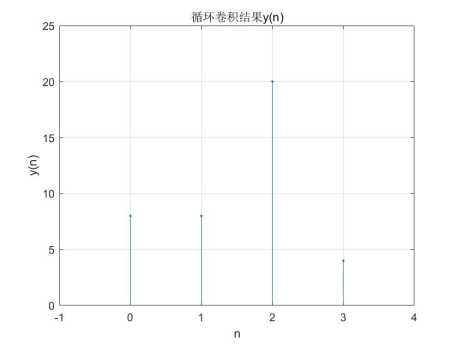
已知两个有限长序列x1= [5,4,-3,-2],x2=[1,2,3,0],用DFT求时域循环卷积y(n)并用图形表示。(利用 matlab作答)
分别求两序列x1、x2的DFT,相乘后求逆变换得到y(n),即为时域循环卷积的结果:
%question 2
clear;
xn1=[5,4,-3,-2];%建立x1(n)序列
xn2=[1,2,3,0];%建立x2(n)祖列
N=length(xn1);
n=0:N-1;k=0:N-1;
Xk1=xn1*(exp(-1j*2*pi/N)).^(n'*k);%由x1(n)的DFT求X1(k)
Xk2=xn2*(exp(-1j*2*pi/N)).^(n'*k);%由x2(n)的DFT求X2(k)
Yk=Xk1.*Xk2;%Y(k)=X1(k)X2(k)
yn=Yk*(exp(1j*2*pi/N)).^(n'*k)/N;%由Y(k)的IDFT求y(n)
yn=abs(yn);%取模值,消除DFT带来的微小复数影响
stem(n,yn,'.');axis([-1,4,0,25])
title('循环卷积结果y(n)');
xlabel('n');ylabel('y(n)');grid on
3.题目三
已知有限长序列x(n) = [1,0.5,0,0.5,1,1,0.5,0],要求:
①用FFT算法求该时域序列的DFT、IDFT的图形;
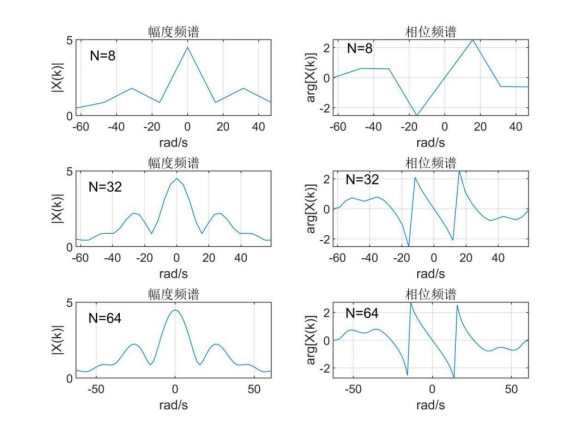
②假定采样频率F =20 Hz,序列长度N分别取8、32和64,使用FFT来计算其幅度频 谱和相位频谱。(利用matlab作答)
使用FFT求得时域序列的DFT,使用IFFT求得时域序列,通过图像对比可发现,由IFFT 求得的时域序列与原序列相同,结果正确。
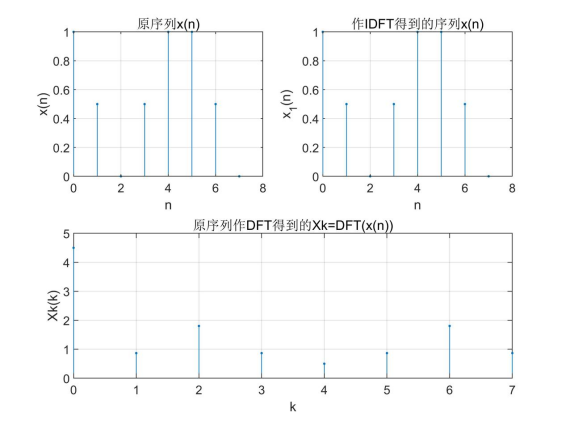
通过fft函数求得采样信号的频谱,并用abs、angle求得幅度频谱和相位频谱,结果如 下:
可看出N取值越大,序列保留得越长,频谱曲线的精度越高。
%question 3
clear;
xn=[1,0.5,0,0.5,1,1,0.5,0];%建立x(n)序列
N=length(xn);
n=0:N-1;k=0:N-1;
Xk=fft(xn,N);%作FFT
xn1=ifft(Xk,N);%作IFFT
subplot(2,2,1);stem(n,xn,'.');
title('原序列x(n)');grid on
xlabel('n');ylabel('x(n)');
subplot(2,1,2);stem(k,abs(Xk),'.');
title('原序列作DFT得到的Xk=DFT(x(n))');grid on
xlabel('k');ylabel('Xk(k)');
subplot(2,2,2);stem(n,xn1,'.');
title('作IDFT得到的序列x(n)');grid on
xlabel('n');ylabel('x_1(n)');
Fs=20;%采样频率Fs=20Hz
N1=8;N2=32;N3=64;%序列长度
D1=2*pi*Fs/N1;%计算模拟频率分辨率
k1=floor(-(N1-1)/2:(N1-1)/2);%频率显示范围对于[-π,π]
D2=2*pi*Fs/N2;%计算模拟频率分辨率
k2=floor(-(N2-1)/2:(N2-1)/2);%频率显示范围对于[-π,π]
D3=2*pi*Fs/N3;%计算模拟频率分辨率
k3=floor(-(N3-1)/2:(N3-1)/2);%频率显示范围对于[-π,π]
Xk1=fftshift(fft(xn,N1));%作FFT且移位π
Xk2=fftshift(fft(xn,N2));%作FFT且移位π
Xk3=fftshift(fft(xn,N3));%作FFT且移位π
figure;
subplot(3,2,1);plot(k1*D1,abs(Xk1))%幅度频谱
title('幅度频谱');xlabel('rad/s');ylabel('|X(k)|');
text(-55,4,'N=8');grid on
subplot(3,2,2);plot(k1*D1,angle(Xk1))%相位频谱
title('相位频谱');xlabel('rad/s');ylabel('arg[X(k)]');
text(-55,2,'N=8');grid on
subplot(3,2,3);plot(k2*D2,abs(Xk2))%幅度频谱
title('幅度频谱');xlabel('rad/s');ylabel('|X(k)|');
text(-55,4,'N=32');grid on
subplot(3,2,4);plot(k2*D2,angle(Xk2))%相位频谱
title('相位频谱');xlabel('rad/s');ylabel('arg[X(k)]');
text(-55,2,'N=32');grid on
subplot(3,2,5);plot(k3*D3,abs(Xk3))%幅度频谱
title('幅度频谱');xlabel('rad/s');ylabel('|X(k)|');
text(-55,4,'N=64');grid on
subplot(3,2,6);plot(k3*D3,angle(Xk3))%相位频谱
title('相位频谱');xlabel('rad/s');ylabel('arg[X(k)]');
text(-55,2,'N=64');grid on
4.题目四
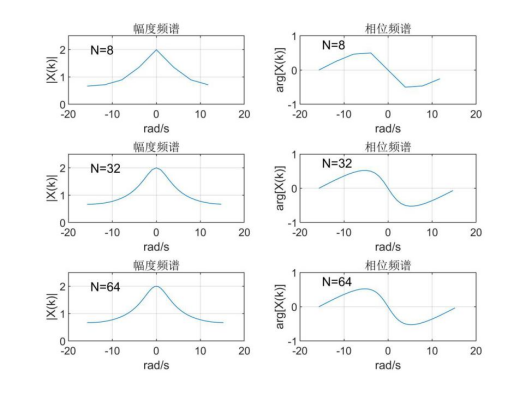
已知一个无限长序列x(n)=0.5n(n≥0),采样周期Ts=0.2 s,要求序列长度N分别取8、32和64,用FFT求其频谱。(利用matlab作答)
由图像可看出N取值越大,序列保留得越长,频谱曲线的精度越高。
%question 4
clear;
Ts=0.2;%采样周期为T=0.2s
N1=[8,32,64];%序列长度N
for r = 0:2
N=N1(r+1);
n=0:N-1;
xn=0.5.^n;%建立x(n)
D=2*pi/(N*Ts);
k=floor(-(N-1)/2:(N-1)/2);
X=fftshift(fft(xn,N));
subplot(3,2,2*r+1);plot(k*D,abs(X));%幅度频谱
title('幅度频谱');xlabel('rad/s');ylabel('|X(k)|');
text(-15,2,['N=',num2str(N)]);axis([-20,20,0,2.5]);grid on
subplot(3,2,2*r+2);plot(k*D,angle(X));%相位频谱
title('相位频谱');xlabel('rad/s');ylabel('arg[X(k)]');
text(-15,0.75,['N=',num2str(N)]);axis([-20,20,-1,1]);grid on
end
5.题目五
已知一个连续时间信号f(t)=sinc(t),取最高有限带宽频率fm=1Hz。(利用matlab作答)
①分别显示原连续时间信号波形和Fs=fm、Fs=2fm、Fs=3fm三种情况下抽样信号的波形;
②求解原连续信号波形和抽样信号所对应的幅度谱;
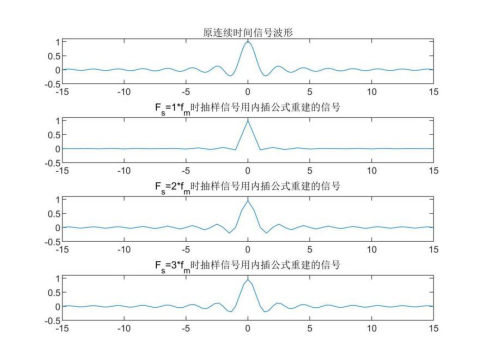
③用时域卷积的方法(内插公式)重建信号;
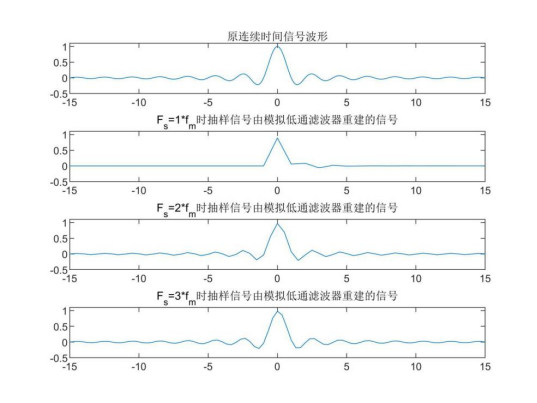
④用模拟低通滤波器重建信号。
在数字信号处理领域中,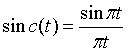 ,因此直接用matlab中的sinc函数直接生成。 当采样频率为1Hz时,即每秒采样一次,除了t=0时,其他时刻均采样在零点,因此当 采样频率
,因此直接用matlab中的sinc函数直接生成。 当采样频率为1Hz时,即每秒采样一次,除了t=0时,其他时刻均采样在零点,因此当 采样频率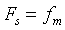 时,其波形除了t=0时不为0外,其他时刻均为0。当
时,其波形除了t=0时不为0外,其他时刻均为0。当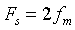 和
和 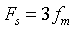 时,能在采样信号的包络上看出原信号的形状。
时,能在采样信号的包络上看出原信号的形状。
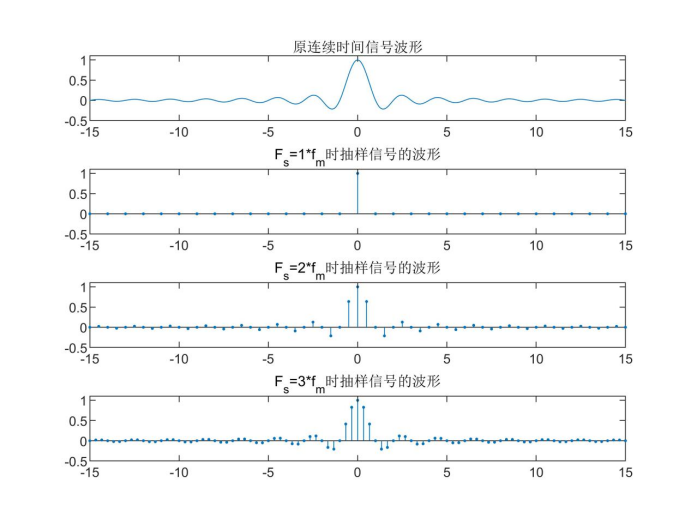
sinc(t)的频谱为矩形窗,当采样频率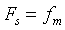 时,并不满足奈奎斯特采样间隔,信号频 谱发生混叠,矩形窗的频谱刚好混叠成一条直线,响应特性H(f)=1。当
时,并不满足奈奎斯特采样间隔,信号频 谱发生混叠,矩形窗的频谱刚好混叠成一条直线,响应特性H(f)=1。当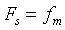 和
和 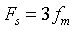 时,满足奈奎斯特采样间隔,信号频谱在
时,满足奈奎斯特采样间隔,信号频谱在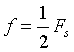 不发生混叠,且频谱在处呈 镜像对称。
不发生混叠,且频谱在处呈 镜像对称。
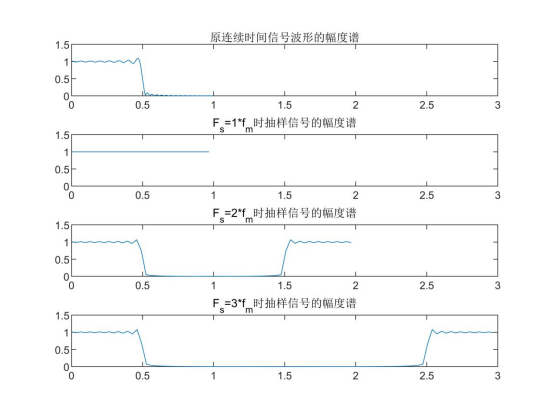
使用内插公式重建信号,结果如下:
当采样频率不满足奈奎斯特间隔时,重建信号明显失真,当采样频率刚好满足奈奎 斯特间隔时,曲线精度较低,但基本恢复出信号的形状,当采样频率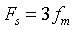 时, 重建出的信号曲线精度较高。
时, 重建出的信号曲线精度较高。
使用模拟滤波器重建信号:
使用matlab自带的切比雪夫Ⅱ型低通滤波器,将原采样信号有限带宽以外的频率 部分滤除,同样可以重建信号。当采样频率不满足奈奎斯特间隔时,重建信号明显 失真,当采样频率刚好满足奈奎斯特间隔时,曲线精度较低,但基本恢复出信号的 形状,当采样频率时,重建出的信号曲线精度较高,与通过内插公式重 建的信号基本相同。实验过程中还发现使用切比雪夫Ⅰ型低通滤波器会导致重建信 号发生时移。
%question 5
clear;
dt=0.1;fm=1;
t=-15:dt:15;
f=sinc(t); %建立原连续信号
figure;
subplot(4,1,1);
plot(t,f);axis([min(t) max(t) -0.5 1.1])
title('原连续时间信号波形');
for i=1:3
fs=i*fm;Ts=1/fs;%确定采样频率和周期
n=-15:Ts:15;
f=sinc(n);%生成抽样信号
subplot(4,1,i+1);stem(n,f,'.');
axis([min(n),max(n),-0.5,1.1]);
title(['F_s=',num2str(i),'*f_m时抽样信号的波形'])
end
dt=0.1;fm=1;
t=-15:dt:15;
f=sinc(t); %建立原连续信号
N=length(t);%求时间轴上的采样点数
wm=2*pi*fm;
k=0:N-1;
w1=k*wm/N;%在频率轴上生成N个采样频率点
F1=f*exp(-1j*t'*w1)*dt;%对原信号进行傅里叶变换
figure;
subplot(4,1,1),plot(w1/(2*pi),abs(F1));
title('原连续时间信号波形的幅度谱');
axis([0,3,0,1.5])
for i=1:3
fs=i*fm;Ts=1/fs;%确定采样频率和周期
n=-15:Ts:15;
f=sinc(n);%生成抽样信号
N=length(n);%求时间轴上采样点数
wm=2*pi*fs;
k=0:N-1;
w=k*wm/N;
F=f*exp(-1j*n'*w)*Ts;%对抽样信号进行傅里叶变换
subplot(4,1,i+1);plot(w/(2*pi),abs(F));
title(['F_s=',num2str(i),'*f_m时抽样信号的幅度谱'])
axis([0,3,0,1.5])
end
dt=0.1;fm=1;
t=-15:dt:15;
f=sinc(t); %建立原连续信号
figure;
subplot(4,1,1);
plot(t,f);axis([min(t) max(t) -0.5 1.1])
title('原连续时间信号波形');
for i=1:3
fs=i*fm;
Ts=1/fs;%确定采样频率和周期
n=-15/Ts:15/Ts;
t1=-15:Ts:15;
f1=sinc(n/fs);%生成抽样信号
T_N=ones(length(n),1)*t1-n'*Ts*ones(1,length(t1));%生成t-nT矩阵
fa=f1*sinc(fs*pi*T_N);%内插公式
subplot(4,1,i+1),plot(t1,fa);
axis([-15,15,-0.5,1.1])
title(['F_s=',num2str(i),'*f_m时抽样信号用内插公式重建的信号'])
end
dt=0.1;fm=1;
t=-15:dt:15;
f=sinc(t); %建立原连续信号
figure;
subplot(4,1,1);
plot(t,f);axis([min(t) max(t) -0.5 1.1])
title('原连续时间信号波形');
N=6;rp=1;as=20;
for i=1:3
fs=i*fm;
Ts=1/fs;%确定采样频率和周期
n=-15:Ts:15;
f=sinc(n);%生成抽样信号
Wp=2*pi*fm;%计算截止角频率
[b,a]=cheby2(N,rp,Wp,'s');%切比雪夫I型
y=lsim(b,a,f,n);
subplot(4,1,i+1),plot(n,y);
axis([-15,15,-0.5,1.1])
title(['F_s=',num2str(i),'*f_m时抽样信号由模拟低通滤波器重建的信号'])
end
6.题目六
6.已知一个时间序列的频谱为:
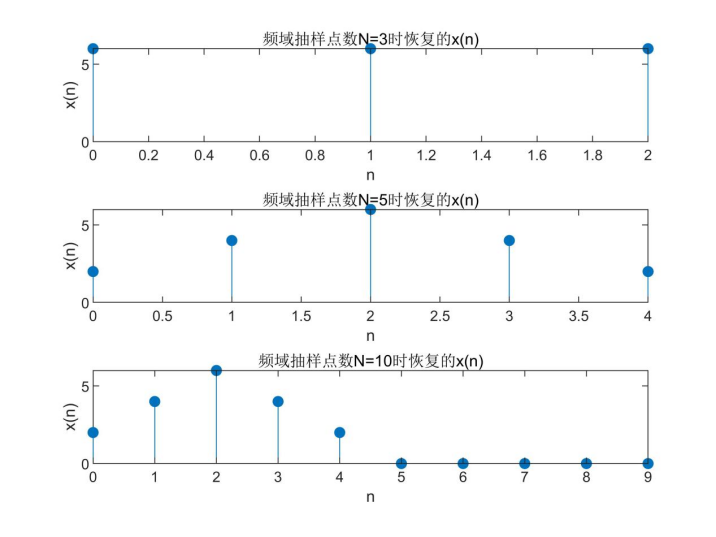
分别取频域抽样点数N为3、5和10,用IFFT计算并求出其时间序列x(n),用图形显示各时间序列。由此讨论原时域信号不失真地由频域抽样恢复的条件。(利用matlab作答)
该题没有给出采样周期Ts的数值,因此取Ts=1。且由频谱表达式可看出时域序列为x(n)=[2,4,6,4,2]。由下面图像可看出,当N=5,N=10时,时间序列未失真,当N=3时,时间序列失真,因此,原时域信号不失真地从频域抽样恢复的条件为:
如果x(n)为有限长序列,且频域抽样点数N大于或等于序列长度M(即N≥M),则从中能无失真地恢复出原信号x(n)。
%question 6
clear;
Ts=1;%默认数字频率为Ts=1
N0=[3,5,10];%给出3种频谱序列的长度N
for r=1:3
N=N0(r);%取N值
D=2*pi/(Ts*N);%求出模拟频率分辨率
kn=floor(-(N-1)/2:-1/2);%建立负频率段向量
kp=floor(0:(N-1)/2);%建立正频率段向量
w=[kp,kn]*D;%将负频率段移到正频率的右端,形成新的频率排序
X=2+4*exp(-1j*w)+6*exp(-1j*2*w)+4*exp(-1j*3*w)+2*exp(-1j*4*w);
n=0:N-1;
x=ifft(X,N);
subplot(3,1,r);stem(n*Ts,abs(x),'filled');
xlabel('n');ylabel('x(n)');
title(['频域抽样点数N=',num2str(N),'时恢复的x(n)'])
end
7.题目七
已知一个频率范围在[ - 6.28,6.28] rad/s间的频谱,在模拟频率=3.14处幅度为1,其它范围幅度均为0。要求计算其连续信号xa(t),并用图形显示信号曲线。(利用matlab作答 )
由奈奎斯特采样定理可知采样频率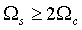 ,即采样周期
,即采样周期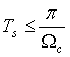 时,就不会发生混叠,选择小一些的采样周期,以增加样点数,取
时,就不会发生混叠,选择小一些的采样周期,以增加样点数,取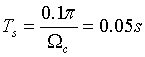 。同时为了使时间信号更加接近连续信号,取点数N=600。求得的连续信号曲线如下:
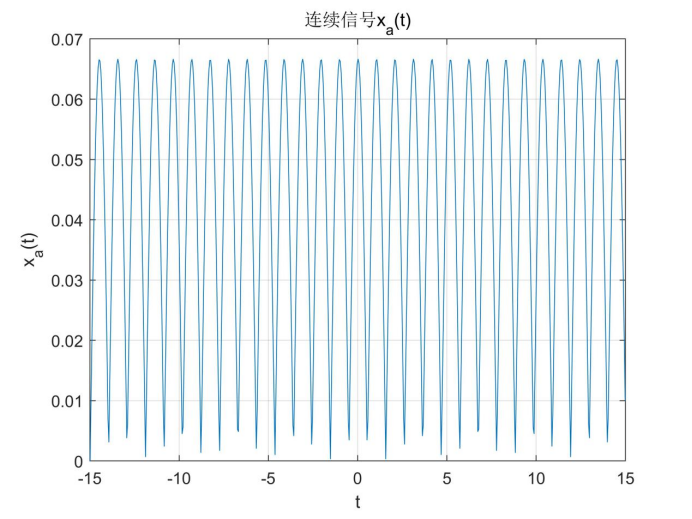
。同时为了使时间信号更加接近连续信号,取点数N=600。求得的连续信号曲线如下:
由分析可得,连续信号应是频率为1Hz的余弦信号,而求得的连续信号曲线在底部有略微失真,推测是频谱上幅度为1对应的频率由略微误差造成的。
%question 7
clear;
wc=6.28;
Ts=0.1*pi/wc;%最大采样周期取临界数值的1/10
N=600;
D=2*pi/(Ts*N);%求模拟频率分辨率
M=floor(wc/D);%求有效频率边界值的下标
Xa=[zeros(1,M/2),1,zeros(1,N-M),1,zeros(1,M/2-1)];
n=-(N-1)/2:(N-1)/2;%建立时间向量
xa=abs(fftshift(ifft(Xa/Ts,N)));
plot(n*Ts,xa);
xlabel('t');ylabel('x_a(t)');
grid on;box on;
title('连续信号x_a(t)');
最后
以上就是娇气帽子最近收集整理的关于数字信号处理实验61.题目一2.题目二3.题目三4.题目四5.题目五6.题目六7.题目七的全部内容,更多相关数字信号处理实验61内容请搜索靠谱客的其他文章。
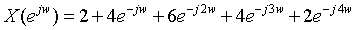








发表评论 取消回复