一、跳表的原理
(一)有序单链表和二分查找法
顾名思义,有序单链表就是节点的排列是有顺序的链表。

如果我们想从中找到一个节点,比如15,除了从头节点开始遍历,是否有其他方式?
经典的查找算法中,有专门针对一个有序的数据集合的算法,即“二分算法”,以O(logN)的时间复杂度进行查找。它通过对比目标数据和中间数据的大小,在每轮查找中直接淘汰一半的数据:
中间节点数字为10(10或8都可以作为中间节点),比目标15小,所以排除10之前的4个数据,在10-21中查找。
中间节点为18 ,比目标15大,排除18及之后的2条数据,在10-15中查找。
中间节点为15 ,与目标一致,查找结束。
设想在链表中,我们参考二分算法的思想,为“中间节点”加索引,就能像二分算法一样进行链表数据的查找了。

OK,现在我们将每一个中间节点抽了出来,组成了另一条链表,即一级索引,一级索引的每个节点都指向原单链表对应的节点,这样可以通过二分算法来快速查找有序单链表中的节点了。
如果原链表节点数量太多将会导致一级索引的节点数量也很多,这时需要继续向上建立索引,选取一级索引的中间节点建立二级索引。
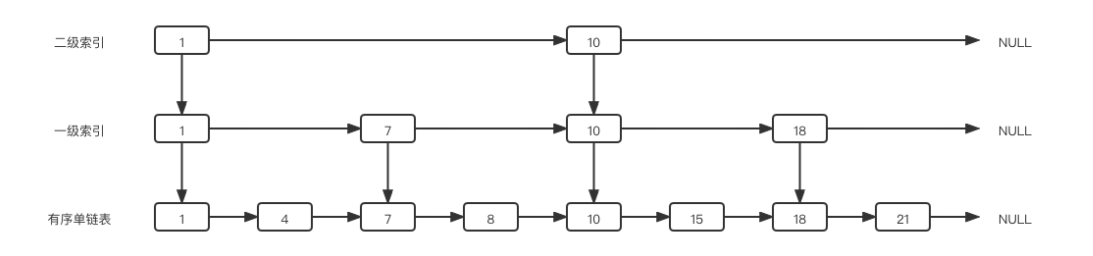
这就是跳表的本质:是对有序链表的改造,为单链表加多层索引,以空间换时间的策略,解决了单链表中查询速度的问题,同时也能快速实现范围查询。
链表节点数少时提升的效果有限,但当链表长度达到1000甚至10000时,从中查找一个数的效率会得到极大的提升。
(二)跳表索引的更新
二叉树和跳表的退化
前言中提到,跳表具有媲美平衡树的效率,平衡树之所以称之为平衡树,是为了解决普通树结构在极端情况下容易退化成一个单链表的问题,每次插入或删除节点时,会维持树的平衡性。
下面这种二叉树具有O(log n) 的查找时间复杂度,但在极端情况下容易发生退化,比如删除了4,5,6三个节点后,会退化为单链表,查询时间复杂度退化为O(n).
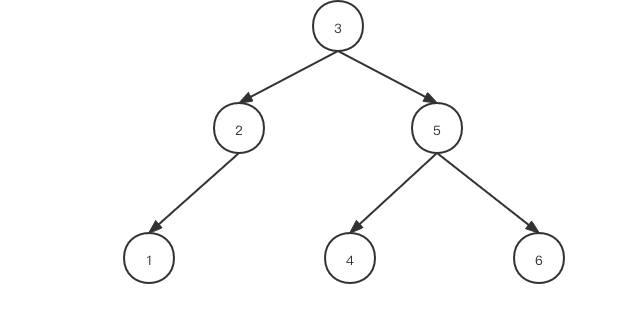
退化后的二叉树:
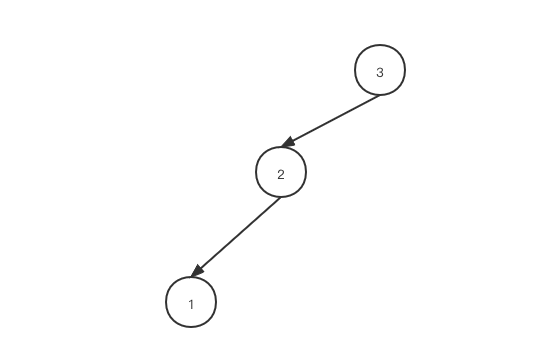
如果跳表在插入新节点后索引就不再更新,在极端情况下,它可能发生退化,比如下面这种情况:

10到100之间插入n多个节点,查询这其中的数据时,查询时间复杂度将退化到接近O(n)。既然跳表被称之为媲美平衡树的数据结构,也必然会维护索引以保证不退化。
跳表索引的维护
通过晋升机制。既然现在跳表每两个原始链表节点中有一个被建立了一级索引,而每两个一级索引中有一个被建立了二级索引,n个节点中有n/2个索引,可以理解为:在同一级中,每个节点晋升到上一级索引的概率为1/2。
如果不严格按照“每两个节点中有一个晋升”,而是“每个节点有1/2的概率晋升”,当节点数量少时,可能会有部分索引聚集,但当节点数量足够大时,建立的索引也就足够分散,就越接近“严格的每两个节点中有一个晋升”的效果。
当然,晋升的概率可以根据需求进行调整,1/3或1/4,晋升概率稍小时,空间复杂度小,但查询效率会降低。在下文中,我们将晋升率设置为p。
(三)时间复杂度与空间复杂度
时间复杂度
结论:跳表的时间复杂度为O(log n)
证明:
按二分法进化出的跳表,无论是原链表还是N级索引,都是每两个节点中有一个被用作上一级索引。这个过程我们称之为“晋升”,晋升的概率为p。
假设原链表节点数量为n,一级索引节点数为n*p^1,二级索引节点数为n*p^2,以此类推,h级索引的节点数应为n*(p^h)。
最高层的期望节点数应为1/p,我的理解是:小于等于这个期望数,再高一层索引的期望节点数将为1,没有意义了。
根据上述推算,易得一个跳表的期望索引高度h为:
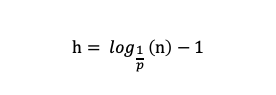
加上底层的原始链表,跳表的期望总高度H为:
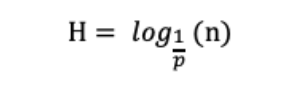
查找索引时,我们运用倒推的思维,从原始链表上的目标节点推到顶层索引的起始节点,示意图如下:
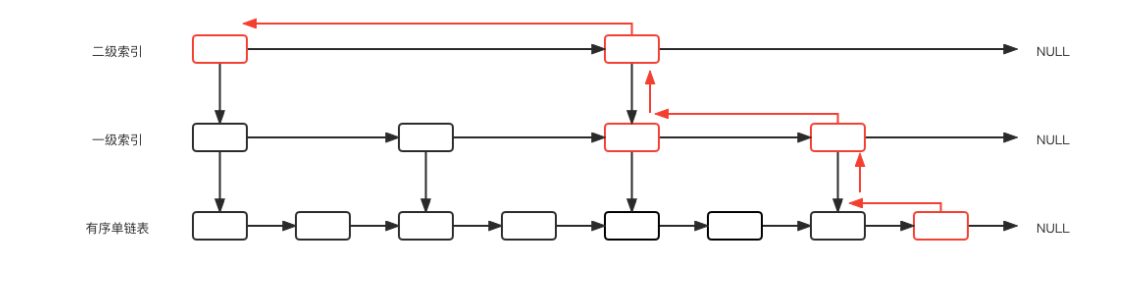
当我们在底层节点时,只有两种路径可走,向上或向左,向上的概率为p,向左的概率为1-p。
假设C(i)为一个无限长度的跳表中向上爬i层的期望代价(即经过的节点数量)
爬到第0层时,无需经过任何节点,所以有:
C(0)=0
爬到第1层时,可能有两种情况:
从有p的概率是从第0层直接爬升1个节点,这种情况经过的节点数为:
(C(0)+1)P
有1-p的概率是从第1层向左移动一个节点,则经过的节点数为:
(C(1)+1)(1+P)
则有:
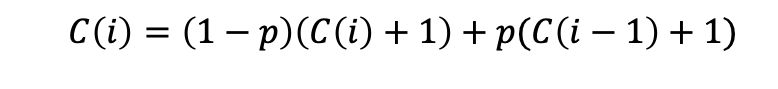
解得:C(i) = i/p
当爬到期望中的最高层——第h层时,则期望步数为h/p,在第h层,继续向左走的期望步数不会超过当前层节点的期望总和1/p,向上走的期望步数也不会超过当前层节点的期望总和1/p,全部加起来,从最底层的目标节点到最顶层的头节点,期望步数为h/p+2/p,将上面h的公式带入,忽略常量,时间复杂度为O(log n)。
空间复杂度
空间复杂度基本上就是等比数列之和的计算,比值为p。
直接说结果为O(n)
二、跳表的实现
为了更好地理解跳表,自己参考着跳表的原理,尝试手撸一条跳表,当然这是最基础的,没有redis跳表那样丰富的能力,粗略实现了对数字的增删改查,以插入的数字作为排序的基准,不支持重复数字的插入。
redis跳表在经典跳表之上有额外的实现:
经典跳表不支持重复值,redis跳表支持重复的分值score。
redis跳表的排序是根据score和成员对象两者共同决定的。
redis跳表的原链表是个双向链表。
在这之前需要说明,索引的节点其实并不是像底层链表一样的节点Node,而是一种Level层结构,每个层中都包含了Node的指针,指向下一个节点。
(一)基础数据结构
package main
const MaxLevel = 32
const p = 0.5
type Node struct {
value uint32
levels []*Level // 索引节点,index=0是基础链表
}
type Level struct {
next *Node
}
type SkipList struct {
header *Node // 表头节点
length uint32 // 原始链表的长度,表头节点不计入
height uint32 // 最高的节点的层数
}
func NewSkipList() *SkipList {
return &SkipList{
header: NewNode(MaxLevel, 0),
length: 0,
height: 1,
}
}
func NewNode(level, value uint32) *Node {
node := new(Node)
node.value = value
node.levels = make([]*Level, level)
for i := 0; i < len(node.levels); i++ {
node.levels[i] = new(Level)
}
return node
}这里的p就是上面提到的节点晋升概率,MaxLevel为跳表最高的层数,这两个数字可以根据需求设定,根据上面推出的跳表高度公式:
可以倒推出此跳表的容纳元素数量上限,n为2^32个。
(二)插入元素
重点在于如何确认插入的这个新节点需要几层索引?通过下面这个函数根据晋升概率随机生成这个新节点的层数。
func (sl *SkipList) randomLevel() int {
level := 1
r := rand.New(rand.NewSource(time.Now().UnixNano()))
for r.Float64() < p && level < MaxLevel {
level++
}
return level
}可以看出,默认层数为1,即无索引,通过随机一个0-1的数,如果小于晋升概率p,且总层数不大于最大层数时,将level+1。
这样就有:
1/2的概率level为1
1/4的概率level为2
1/8的概率level为3
......
这里需要注意一下,上面我们说有1/2的概率有一层索引,即level为2的概率应该是1/2,为什么这里是1/4呢?而位于第一层的原始链表存在的概率应该是1,这里为什么level=1的概率为1/2呢?
原因在于,当level为2时,同时也表示存在第一层;当level为3时,同时也存在第一层和第二层;毕竟不能出现“空中阁楼”。所以:
新节点存在原链表节点的概率为1/2+1/4+1/8+...=1
新节点存在一层索引的概率为1/4+1/8+1/16+...=1/2
新节点存在二层索引的概率为1/8+1/16+1/32+...=1/4
插入元素的具体代码如下:
func (sl *SkipList) Add(value uint32) bool {
if value <= 0 {
return false
}
update := make([]*Node, MaxLevel)
// 每一次循环都是一次寻找有序单链表的插入过程
tmp := sl.header
for i := int(sl.height) - 1; i >= 0; i-- {
// 每次循环不重置 tmp,直接从上一层确认的节点开始向下一层查找
for tmp.levels[i].next != nil && tmp.levels[i].next.value < value {
tmp = tmp.levels[i].next
}
// 避免插入相同的元素
if tmp.levels[i].next != nil && tmp.levels[i].next.value == value {
return false
}
update[i] = tmp
}
level := sl.randomLevel()
node := NewNode(uint32(level), value)
// fmt.Printf("level:%v,value:%v\n", level, value)
if uint32(level) > sl.height {
sl.height = uint32(level)
}
for i := 0; i < level; i++ {
// 说明新节点层数超过了跳表当前的最高层数,此时将头节点对应层数的后继节点设置为新节点
if update[i] == nil {
sl.header.levels[i].next = node
continue
}
// 普通的插入链表操作,修改新节点的后继节点为前一个节点的后继节点,修改前一个节点的后继节点为新节点
node.levels[i].next = update[i].levels[i].next
update[i].levels[i].next = node
}
sl.length++
return true
}数组update保存了每一层对应的插入位置。
从头节点的最高层开始查询,每次循环都可以理解为一次寻找有序单链表插入位置的过程。
找到在这层索引的插入位置,存入update数组中。
遍历完一层后,直接使用这一层查到的节点,即代码中的tmp开始遍历下一层索引。
重复1-3步直到结束。
获取新节点的层数,以确定从哪一层开始插入。如果层数大于跳表当前的最高层数,修改当前最高层数。
遍历update数组,但只遍历到新节点的最大层数。
增加跳表长度,返回true表示新增成功。
比如下面这张跳表,我要新增元素9,最高高度为5,当前最高高度为3:
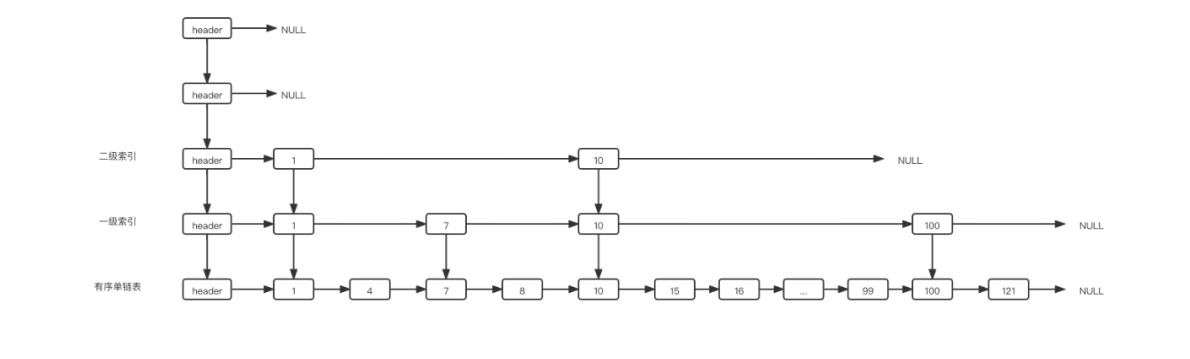
update长度为5
那么会从3层开始向下遍历,在二级索引这层找到9应该插入的位置——1和10之间,update[2]记录包含1的节点。
在一级索引这层找到9应该插入的位置——7和10之间,update[1]记录了包含7的节点。
在原链表这层找到9应该插入的位置——8和10之间,update[0]记录了包含8的节点。
假设新节点的level为4,则修改当前最高高度为4,然后开始逐层插入这个新节点,update[3]为空,因为目前整个跳表的高度只有3,所以需要将三级索引上的节点9插入到头节点后面,插入过程与普通的链表插入无异。示意图如下:
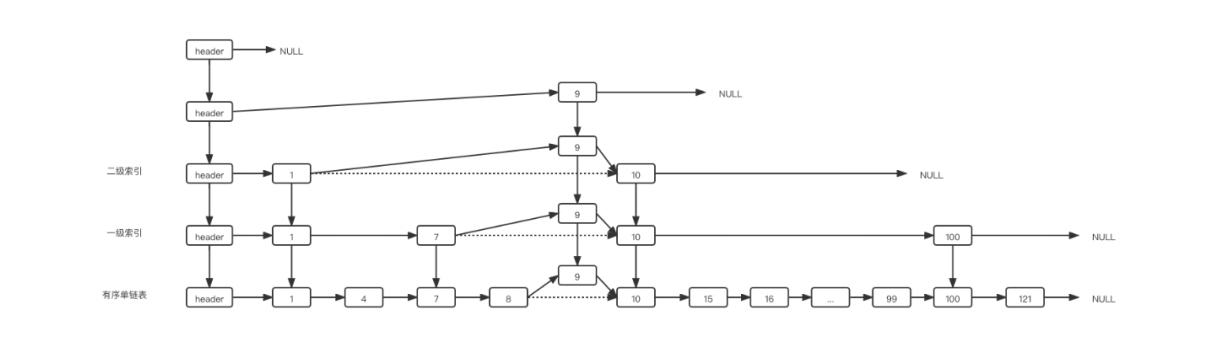
(三)删除元素
func (sl *SkipList) Delete(value uint32) bool {
var node *Node
last := make([]*Node, sl.height)
tmp := sl.header
for i := int(sl.height) - 1; i >= 0; i-- {
for tmp.levels[i].next != nil && tmp.levels[i].next.value < value {
tmp = tmp.levels[i].next
}
last[i] = tmp
// 拿到 value 对应的 node
if tmp.levels[i].next!=nil&&tmp.levels[i].next.value == value {
node = tmp.levels[i].next
}
}
// 没有找到 value 对应的 node
if node == nil {
return false
}
// 找到所有前置节点后需要删除node
for i := 0; i < len(node.levels); i++ {
last[i].levels[i].next = node.levels[i].next
node.levels[i].next = nil
}
// 重定向跳表高度
for i := 0; i < len(sl.header.levels); i++ {
if sl.header.levels[i].next == nil {
sl.height = uint32(i)
break
}
}
sl.length--
return true
}与插入节点思路一致,从最上层开始向下遍历寻找,找到需要删除的节点的前置节点并记录在 last 数组中,然后修改前置节点指针的指向。
(四)查找
解决了增删,剩下的查询就很简单了,可以查找对应value的node,也可以查找一个范围。
查找范围即先找到范围前边界的节点,再通过链表向后遍历即可。
这里我只实现了查找单个node的函数:
func (sl *SkipList) Find(value uint32) *Node {
var node *Node
tmp := sl.header
for i := int(sl.height) - 1; i >= 0; i-- {
for tmp.levels[i].next != nil && tmp.levels[i].next.value <= value {
tmp = tmp.levels[i].next
}
if tmp.value == value {
node = tmp
break
}
}
return node
}三、redis的跳表实现
上述是一个标准跳表的原理和实现,redis中的跳表还有所不同,它提供了更多的特性和能力:
经典跳表不支持重复值,redis跳表支持重复的分值score。
redis跳表的排序是根据score和成员对象两者共同决定的。
redis跳表的原链表是个双向链表。
redis中,跳表只在zset结构有使用。zset结构在成员较少时使用压缩列表 ziplist作为存储结构,成员达到一定数量后会改用map+skiplist作为存储结构。这里只讨论使用skiplist的实现。
zset结构要求,分值可以相同,但保存的成员对象不能相同。zset对跳表排序的依据是“分值和成员对象”两个维度,分值可以相同,但成员对象不能一样。分值相同时,按成员对象首字母在字典的顺序确定先后。
zset还维护了一个map,保存成员对象与分值的映射关系,被用来通过成员对象快速查找分值,定位对应的节点,在ZRANK、ZREVRANK、ZSCORE等命令中均有使用。
另外,这个map还用于插入节点时,判断是否存在重复的成员对象。见下面redis源码中的dictFind函数。
int zsetAdd(robj *zobj, double score, sds ele, int in_flags, int *out_flags, double *newscore) {
// ...
/* Update the sorted set according to its encoding. */
if (zobj->encoding == OBJ_ENCODING_ZIPLIST) {
// ...
} else if (zobj->encoding == OBJ_ENCODING_SKIPLIST) {
zset *zs = zobj->ptr;
zskiplistNode *znode;
dictEntry *de;
de = dictFind(zs->dict, ele);
if (de != NULL) {
// 已经存在
// ...
} else if (!xx) {
// 不存在,插入
ele = sdsdup(ele);
znode = zslInsert(zs->zsl, score, ele);
serverAssert(dictAdd(zs->dict,ele, &znode->score) == DICT_OK);
*out_flags |= ZADD_OUT_ADDED;
if (newscore) *newscore = score;
return 1;
} else {
*out_flags |= ZADD_OUT_NOP;
return 1;
}
}
}四、回顾问题
前面提到,在看《Redis设计与实现》这本书时我有几点疑问,在详细了解跳表之后现在就完全理解了。
(一)为什么表头节点是不被计算在length属性里?
因为表头节点是初始化跳表时提供的空节点,不保存任何节点,只用于提供各级索引的入口。
(二)新增节点时是如何决定level的指针指向哪个后继节点?
通过分值和成员对象共同决定,判断新节点的插入位置和顺序。分值相同时,按成员对象首字母在字典的顺序确定先后。
经典跳表也同样需要一个维度来确定插入的顺序,我的跳表实现中直接使用了新节点的值作为排序的维度。
(三)为什么zset分值可以相同而成员对象不能相同?
根据第二个问题的答案,如果都相同,就无法确定插入的位置和顺序。
最后
以上就是岁月静好最近收集整理的关于跳表原理及其Golang实现的全部内容,更多相关跳表原理及其Golang实现内容请搜索靠谱客的其他文章。








发表评论 取消回复