曲线上点的曲率半径计算

112 阅读 0 评论 74 点赞

我是靠谱客的博主美满灰狼，最近开发中收集的这篇文章主要介绍曲线上点的曲率半径计算，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

在微分几何中，曲率的倒数就是曲率半径，即R=1/K。平面曲线的曲率就是针对曲线上某个点的切线方向角对弧长的转动率，通过微分来定义，表明曲线偏离直线的程度。对于曲线，它等于最接近该点处曲线的圆弧的半径。对于表面，曲率半径是最适合正常截面或其组合的圆的半径。

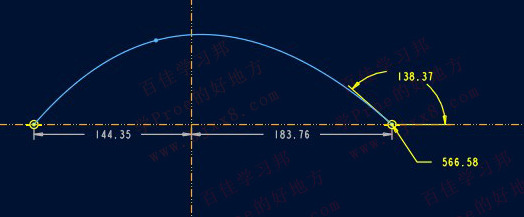
曲率半径主要是用来描述曲线上某处曲线弯曲变化的程度，特殊的如：圆上各个地方的弯曲程度都是一样的故曲率半径就是该圆的半径；直线不弯曲，和直线在该点相切的圆的半径可以任意大，所以曲率是0，故直线没有曲率半径。

圆形半径越大，弯曲程度就越小，也就越近似于一条直线。所以说，曲率半径越大曲率越小，反之亦然。

如果对于某条曲线上的某个点可以找到一个与其曲率相等的圆形，那么曲线上这个点的曲率半径就是该圆形的半径（注意，是这个点的曲率半径，其他点有其他的曲率半径)。也可以这样理解：就是把那一段曲线尽可能地微分，直到最后近似为一个圆弧，此圆弧所对应的半径即为曲线上该点的曲率半径。

曲率半zhidao径的公式为κ=lim|Δα/Δs|。

ρ=|[(1+y'^2)^(3/2)]/y"|

如果给定一段曲线上三个点的坐标，就可以计算出该点的曲率半径

代码

package com.example.maventest.scort.curvartureRadius;
import javafx.geometry.Point2D;
public class CurvartureRadius {
public static void main(String[] args) {
Point2D point2D1 = new Point2D(0, 1);
Point2D point2D2 = new Point2D(1, 1);
Point2D point2D3 = new Point2D(1, 2);
double curvartureRadius = CurvartureRadius.getCurvartureRadius(point2D1, point2D2, point2D3);
System.out.println(curvartureRadius);
}
/**
* 曲率半径计算
*
* @param p1 点1
* @param p2 点2
* @param p3 点3
* @return
*/
public static double getCurvartureRadius(Point2D p1, Point2D p2, Point2D p3) {
Point2D v12 = p2.subtract(p1);
Point2D v23 = p2.subtract(p2);
//three point on the same line,the curvature radius is infinite, return 99999.0
if (v12.normalize().equals(v23.normalize())) {
return 99999.0;
}
double x1, x2, x3, y1, y2, y3, x12, y12, x23, y23;
double x0, y0;
x1 = p1.getX();
x2 = p2.getX();
x3 = p3.getX();
y1 = p1.getY();
y2 = p2.getY();
y3 = p3.getY();
x12 = (x1 + x2) / 2;
y12 = (y1 + y2) / 2;
x23 = (x2 + x3) / 2;
y23 = (y2 + y3) / 2;
if (v12.getY() == 0) {
x0 = x12;
y0 = ((y3 + y2) - (Math.pow(x2 - x0, 2) - Math.pow(x3 - x0, 2)) / (y3 - y2)) / 2;
} else if (v23.getY() == 0) {
x0 = x23;
y0 = ((y1 + y2) - (Math.pow(x2 - x0, 2) - Math.pow(x1 - x0, 2)) / (y1 - y2)) / 2;
} else {
double k12 = -v12.getX() / v12.getY();
double k23 = -v23.getX() / v23.getY();
x0 = (y23 - y12 - k23 * x23 + k12 * x12) / (k12 - k23);
y0 = (x0 - x12) * k12 + y12;
}
double R = Math.sqrt(Math.pow((x1 - x0), 2) + Math.pow((y1 - y0), 2));
return R;
}
}